Natural Numbers Formula: Natural numbers, constituting a fundamental subset of the number system, encompass all positive integers starting from 1 and extending infinitely. Termed "counting numbers," they exclusively encompass positive values and lack representation of zero or any negative figures. This category falls within the domain of real numbers, encompassing solely positive whole numbers while excluding zero, fractions, decimals, and negative integers. The ensuing section will delve into the definition of natural numbers and provide illustrative instances for better comprehension.
Also Check -
Introduction to Graph Formula
What are Natural Numbers?
Natural numbers encompass the entirety of whole numbers, excluding the value 0. These numerical entities hold immense significance in our daily routines. Numerals permeate our surroundings, serving various purposes such as tallying items, denoting currency values, gauging temperature, indicating time, and more. The specific subset of numbers employed for item enumeration is labeled as 'natural numbers'. For instance, when quantifying objects, we express quantities like 5 cups, 6 books, 1 bottle, and similar instances.
Also Check -
Line and Angles Formula
Natural Numbers Definition
Natural numbers constitute the numerical entities employed for the act of counting and hold a position within the realm of real numbers. This collection of natural numbers exclusively encompasses positive integers, represented as 1, 2, 3, 4, 5, 6, and so forth, extending infinitely.
Examples of Natural Numbers
:
Here are a few examples of natural numbers: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, and so on.
Set of Natural Numbers:
In the realm of Mathematics, a set denotes an assemblage of elements, with numbers being relevant in this context. The set of natural numbers is symbolically represented as {1, 2, 3, ...}, signifying an unending sequence.
Also Check -
Ratio and proportion Formula
Natural Numbers Symbol
In the realm of Mathematics, a set denotes an assemblage of elements, with numbers being relevant in this context. The set of natural numbers is symbolically represented as {1, 2, 3, ...}, signifying an unending sequence.
|
Statement Form
|
N = Set of all numbers starting from 1.
|
|
Roaster Form
|
N = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ………………………………}
|
|
Set Builder Form
|
N = {x : x is an integer starting from 1}
|
Smallest Natural Number
Indeed, the smallest natural number is universally acknowledged as 1. Within the context of the set of natural numbers (denoted as N), it is established that the smallest element present is 1. This fundamental observation indicates that the sequence of natural numbers commences at 1 and continues endlessly towards infinity.
Natural Numbers from 1 to 100
The natural numbers encompassed within the range of 1 to 100 are listed as follows: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, and 100.
Is 0 a Natural Number?
Correct, 0 is not considered a natural number because natural numbers are specifically defined as counting numbers. When counting objects, the enumeration begins with 1 and does not include 0. Therefore, 0 does not fall within the category of natural numbers.
Also Check -
Sequence and Series Formula
ODD Numbers and EVEN Numbers
Odd natural numbers are those that are not divisible by 2 and are part of the set of natural numbers, denoted as N. Therefore, the collection of odd natural numbers can be represented as {1, 3, 5, 7, ...}.
On the other hand, even natural numbers are precisely those natural numbers that can be divided by 2 without leaving a remainder. They also belong to the set of natural numbers, N. The set of even natural numbers is depicted as {2, 4, 6, 8, ...}.
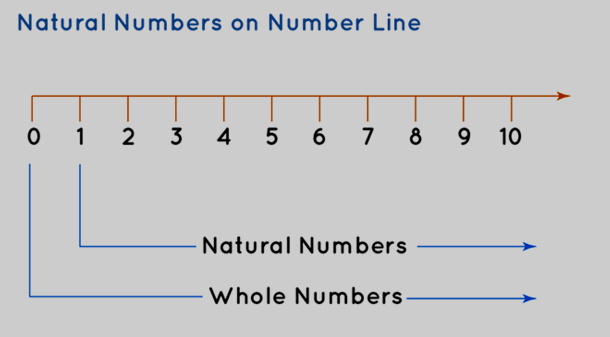
Natural Numbers on Number Line
The arrangement of natural numbers and whole numbers can be visually represented on a number line as depicted below. The positive integers, situated on the right side of zero, symbolize the natural numbers. Conversely, the positive integers combined with zero constitute the whole numbers.
(Number line illustration with natural numbers and whole numbers)
Properties of Natural Numbers
The arithmetic operations of addition, subtraction, multiplication, and division applied to natural numbers yield four fundamental properties. These properties are elucidated below:
Closure Property:
The addition and multiplication of two natural numbers always result in another natural number. This property applies to addition and multiplication, but not to subtraction and division.
Associative Property:
The sum or product of any trio of natural numbers remains invariant, regardless of how the numbers are grouped. This property is applicable to addition and multiplication, but not to subtraction and division.
Commutative Property:
The outcome of adding or multiplying two natural numbers remains unaltered even if the order of the numbers is interchanged. This property applies to addition and multiplication, but not to subtraction and division.
Distributive Property:
The distributive law of multiplication over addition and subtraction states that an expression in the form of a (b + c) can be evaluated as a × b + a × c. This property holds for both addition and subtraction.
In multiplication, distributive property over addition is given by a × (b + c) = (a × b) + (a × c).
In multiplication, distributive property over subtraction is given by a × (b - c) = (a × b) - (a × c).
These properties are crucial in understanding the behavior of arithmetic operations on natural numbers and contribute to mathematical reasoning and problem-solving.
Important Points
-
0 is not a natural number, it is a whole number.
-
Negative numbers, fractions, and decimals are neither natural numbers nor whole numbers.
Natural Numbers Examples
Example 1:
Identify the natural numbers among the following numbers: -1, 0, 3, 1/2, 5.
Solution:
The set of natural numbers in Mathematics is the set {1, 2, 3, ...}. Now, -1 is a negative number, so it is not a natural number. 0 is also not a natural number. 1/2, being a fractional number, is not a natural number, either. Therefore, among the given numbers, the natural numbers are 3 and 5.
Example 2:
Fill in the blanks with respect to natural numbers.
a.) Natural numbers start from _
b.) _ is a whole number which is not a natural number.
c.) Write the natural numbers from 2 to 12
Solution:
a.) Natural numbers start from 1
b.) 0 is a whole number which is not a natural number.
c.) The natural numbers from 2 to 12 can be listed as follows: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
Example 3:
State true or false with respect to natural numbers.
a.) 0 is a natural number.
b.) Every natural number is a whole number.
c.) All natural numbers are integers.
Solution:
a.) False, 0 is not a natural number. It is a whole number.
b.) True, every natural number is a whole number because whole numbers include all positive counting numbers ranging from 0.
c.) True, all natural numbers are integers because integers include all positive numbers, all negative numbers, and zero.
