NCERT Solutions for Class 12 Maths Chapter 10 Exercise 10.4 (Vector Algebra)
NCERT Solutions for Class 12 Maths Chapter 10 Exercise 10.4 contains all the questions with detailed solutions. Students are advised to solve these questions for better understanding of the concepts in exercise 10.4.
Krati Saraswat1 Mar, 2024
Share
NCERT Solutions for Class 12 Maths Chapter 10 Exercise 10.4 (Vector Algebra): NCERT Solutions for Class 12 Maths Chapter 10 Exercise 10.4 are all about working with vectors. Vectors are used to represent quantities that have both magnitude and direction, like forces or velocities. In this exercise, you'll learn how to multiply vectors both in a regular way and in a special way called dot product and cross product. These operations are useful in geometry and physics to solve problems involving distances, angles, forces, and motion. The solutions provided in this exercise help you understand these concepts better and solve problems step by step. By practicing with these solutions, you'll become more confident in dealing with vector problems and improve your math skills.
NCERT Solutions for Class 12 Maths Chapter 10 Exercise 10.4 Overview
NCERT Solutions for Class 12 Maths Chapter 10 Exercise 10.4 of Vector Algebra is prepared by the academic team of Physics Wallah. We have prepared NCERT Solutions for all exercise of Chapter 10. Given below are step-by-step solutions to all questions given in the NCERT Solutions for Class 12 Maths Chapter 10 Exercise 10.4.
NCERT Solutions for Class 12 Maths Chapter 10 Miscellaneous Exercise
NCERT Solutions for Class 12 Maths Chapter 10 Exercise 10.4
Solve The Following Questions. Question 1. Find |.png)
x
.png)
| if
Solution :
We have,
NCERT Solutions for Class 12 Maths Chapter 10 Exercise 10.1
Question 2. Find a unit vector perpendicular to each of the vectors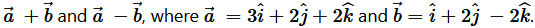
Solution :
We have
NCERT Solutions for Class 12 Maths Chapter 10 Exercise 10.2
Question 3. If a unit vector
makes an angle π/3 with
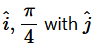and an acute angle θ with
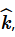then find θ and hence, the components of
.
Solution :
Let unit vector
have (
a
1
,
a
2
,
a
3
) components.
NCERT Solutions for Class 12 Maths Chapter 10 Exercise 10.3
Question 4. Show that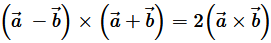
Solution :
Question 5. Find λ and μ if
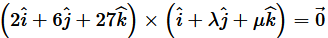Solution :
Question
6. Given that
.
= 0 and
x
= 0 What can you conclude about the vectors
and
?
Solution :
.
= 0
Then,
(i)
Either |
| = 0 or |
| = 0, or
⊥
(in case
and
are non - zero)
x
= 0
(ii)
Either |
| = 0 or |
| = 0 or
||
(in case
and
are non - zero)
But,
and
cannot be perpendicular and parallel simultaneously.
Hence |
| = 0 or |
| =0.
Question
7. Let the vectors
,
,
.png)
be given as
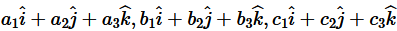then show that
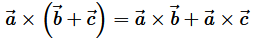Solution :
We have
,
Hence, the given result is proved.
Question
8. It either
= 0 and
= 0 then
x
= 0 Is the converse true? Justify your answer with an example.
Solution :
Take any parallel non-zero vectors so that
x
= 0
Hence, the converse of the given statement need not be true.
Question
9. Find the area of the triangle with vertices A (1, 1, 2), B (2, 3, 5) and C (1, 5, 5).
Solution :
The vertices of triangle ABC are given as A (1, 1, 2), B (2, 3, 5), and
C (1, 5, 5).
The adjacent sides
and
of ΔABC are given as:
Hence, the area of ΔABC is √61/2 sq. units.
Question
10. Find the area of the parallelogram whose adjacent sides are determined by the vectors
Solution :
The area of the parallelogram whose adjacent sides are
and
is |
x
|.
Adjacent sides are given as:
Hence, the area of the given parallelogram is 15√2 sq. units.
Question
11. Let the vectors
and
such that |
| = 3 and |
| = √2/3 then
x
is a unit vector, if the angle between
and
is:
(A) π/6
(B) π/4
(C) π/3
(D) π/2
Solution :
It is given that |
| = 3 and |
| = √2/3
We know that
x
= |
||
|sin
θ
, where n is a unit vector perpendicular to both
and
and
θ
is the angle between
and
.
Now,
x
is a unit vector if
|
x
| = 1
Therefore, option (B) is correct.
Question
12. Area of a rectangle having vertices A, B, C and D with position vectors
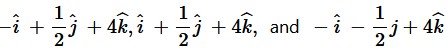respectively is:
(A) 1/2
(B) 1
(C) 2
(D) 4
Solution :
The position vectors of vertices A, B, C, and D of rectangle ABCD are given as:
The adjacent sides
and
of the given rectangle are given as:
Now, it is known that the area of a parallelogram whose adjacent sides are
and
is
|
x
|
.
Hence, the area of the given rectangle is |
x
| = 2 sq. units.
Therefore, option (C) is correct.
NCERT Solutions for Class 12 Maths Chapter 10 Exercise 10.4 FAQs
What are some important properties of dot (scalar) product?
Some important properties of dot product include commutativity, distributivity, and the fact that the dot product of two vectors is zero if the vectors are perpendicular to each other.
How do I find the cross (vector) product of two vectors?
To find the cross product of two vectors, you can use the determinant method or the component method. Practice solving problems and applying the formulas for cross product to become familiar with the process.
What are the applications of vector algebra in geometry and physics?
Vector algebra has numerous applications in geometry and physics, including calculating distances, determining angles between lines or planes, solving problems related to forces and velocities, and analyzing motion in three-dimensional space.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
