
A Parabola is a U-shaped curve that is mirror-symmetrical. In mathematics, a parabola is often defined as the set of points that are equidistant from a fixed point (the focus) and a fixed straight line (the directrix). There are two types of parabolas: upward-opening and downward-opening, depending on the orientation of the U-shape.
What is Parabola?
"A parabola is a curve defined by an equation in which each point on the curve is at an equal distance from a fixed point, known as the 'focus,' and a fixed line, referred to as the 'directrix.' It's essential to note that the focus point does not coincide with the directrix line. In mathematical terms, a parabola is the locus of points equidistant from a given focus and a given directrix, making it a significant curve in the realm of coordinate geometry and conic sections."
Parabola Equation
The general equation of a parabola is: y = a(x-h) 2 + k or x = a(y-k) 2 +h, where (h,k) denotes the vertex. The standard equation of a regular parabola is y 2 = 4ax.
The general equation of a parabola is:
y = a(x - h) 2 + k (regular)
x = a(y – k) 2 + h (sideways)
Where,
(h, k) = vertex of the parabola
Focus: The focus of a parabola is a fixed point, typically denoted as (a, 0).
Directrix: The directrix is a fixed line, often represented as a vertical line passing through the point (-a, 0). The directrix is perpendicular to the axis of the parabola.
Focal Chord: A focal chord is a straight line that passes through the focus of the parabola. It intersects the parabola at two distinct points.
Focal Distance: The focal distance is the distance between a point on the parabola and the focus. It is also equal to the perpendicular distance from that point to the directrix.
Latus Rectum: The latus rectum is a focal chord that is perpendicular to the axis of the parabola. It passes through the focus and is characterized by its length, which is typically 4a. The endpoints of the latus rectum are (a, 2a) and (a, -2a).
Eccentricity: The eccentricity (e) of a parabola is always equal to 1. It represents the ratio of the distance of a point on the parabola from the focus to the distance of that point from the directrix.
These terms and features are fundamental for understanding and working with parabolas in various mathematical and practical applications, providing insights into their characteristics and properties.

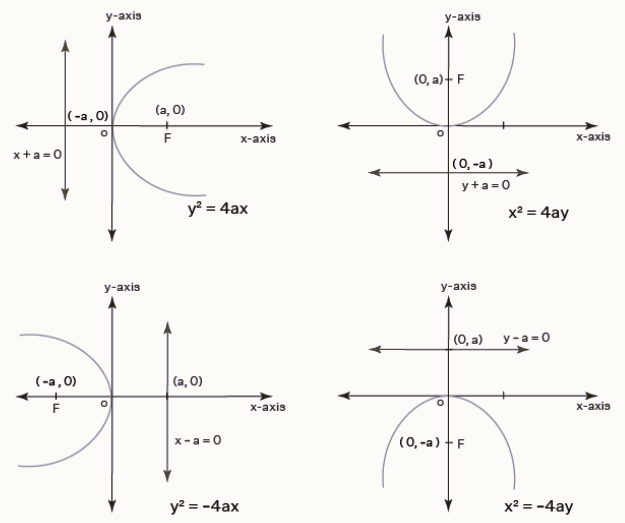
Standard Equations of a Parabola
There are four standard equations of a parabola.
- y 2 = 4ax
- y 2 = -4ax
- x 2 = 4ay
- x 2 = -4ay
Parabola Formula
Parabola formulas are essential for representing the general characteristics of parabolic paths in a plane. They provide the mathematical expressions to determine various parameters of a parabola. Some of the key formulas include:
|
Parabola Formulas |
||
| Equation | y = a(x - h) 2 + k | x = a(y - k) 2 +h |
| Axis of Symmetry | x = h | y = k |
| Vertex | (h, k) | (h, k) |
| Focus | (h, k + (1/4a)) | (h + (1/4a), k) |
| Directrix | y = k - 1/4a | x = h - 1/4a |
| Direction of Opening | Up (a > 0) or Down (a < 0) | Right (a > 0) or Left (a < 0) |
| Length of Latus Rectum | 1/a | 1/a |
| Does it Have Max or Min? | Max if a < 0 Min if a > 0 | Not Applicab |
Graphing Parabola
Consider an equation y = 3x 2 - 6x + 5. For this parabola, a = 3 , b = -6 and c = 5. Here is the graph of the given quadratic equation, which is a parabola.
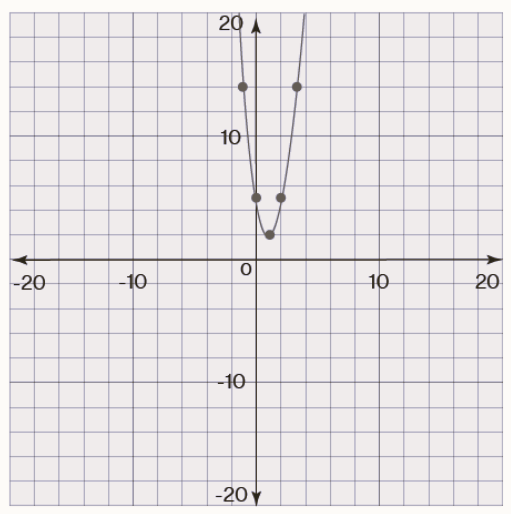
Direction: Here a is positive, and so the parabola opens up.
vertex = (h, k)
h = -b/2a
= 6/(2 ×3) = 1
k = f(h)
= f(1) = 3(1) 2 - 6 (1) + 5 = 2
Thus vertex is (1, 2)
Length of latus rectum = 1/a = 1/3
Focus: (h, k + 1/4a) = (1,25/12)
Axis of symmetry is x =1
Directrix: y = k-1/4a
y = 2 - 1/12 ⇒ y - 23/12 = 0
Derivation of Parabola Equation
Take a point P with coordinates (x,y) on the parabola which lies on the X-Y plane. By the definition of the parabola, the distance of any point on the parabola from the focus and from the directrix is equal. Now distance of P from the directrix is given by PB where the coordinates of B are (-a, y) as it lies on the directrix, and the distance of P from focus is PF, which is represented by the following diagram:
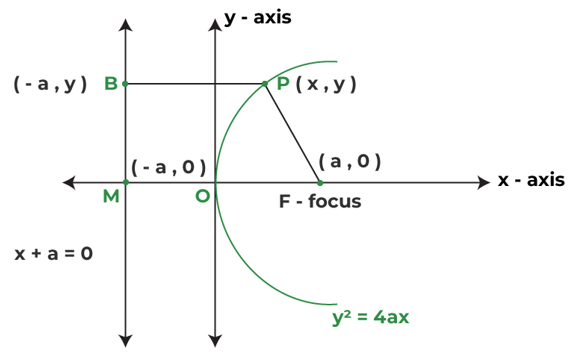
By the definition of parabola, PF = PB ....(1)
Using the distance formula, we get
PF = √(x−a)2+(y−0)2= √{(x−a)2+y2} ....(2)
PB = √{(x+a)2} ....(3)
By using, equations (1), (2), and (3), we get
√{(x−a)2+y2} = √{(x+a)2}
⇒ (x – a)2 + y2 = (x + a)2
⇒ x2 + a2 – 2ax + y2 = x2 + a2 + 2ax
⇒ y2 – 2ax = 2ax
y2 = 4ax
Which is the required equation of the parabola.
Similarly, the equation for other parabolas i.e., x2 = 4ay, y2 = -4ax, and x2 = -4ay, can also be proved.
Parabola Formula Applications
Physics and Engineering:
- Projectile Motion: The path of a projectile (such as a thrown object or a launched missile) follows a parabolic trajectory. The parabola formula is used to model and analyze the motion of projectiles.
- Optics: Parabolic mirrors and lenses are used in optical systems to focus or direct light. The shape of a parabola allows it to reflect or refract parallel rays to a common focus point.
Architecture and Design:
- Architecture: Parabolic arches and domes are used in architectural design to create aesthetically pleasing and structurally sound buildings. The parabola's properties make it an ideal shape for distributing forces evenly.
- Satellite Dishes: The dish of a satellite antenna is often shaped as a parabolic reflector. This shape helps focus incoming signals onto the receiver at the focal point.
Electronics and Technology:
- Antenna Design: Parabolic antennas, including satellite dishes and radar systems, use the parabola formula to design and position the reflector surface for optimal signal reception or transmission.
- Signal Processing: In signal processing and image processing, parabolic curves can be used to fit data and extract valuable information.
Mathematics and Education:
- Teaching and Learning: The parabola formula is a fundamental concept in algebra and calculus education. It's often one of the first quadratic equations students encounter, helping them understand key mathematical concepts.
- Graphing and Analysis: In mathematics, parabolas are essential for graphing quadratic functions and solving equations. They also play a role in the study of conic sections.
Finance and Economics:
- Cost-Volume-Profit Analysis: In business and economics, the cost-volume-profit (CVP) analysis often involves parabolic cost functions. These functions help businesses determine their profit-maximizing production levels.
Astrophysics:
- Gravitational Lensing: Parabolas can be used to model gravitational lensing, a phenomenon in astrophysics where the gravity of massive objects, such as black holes or galaxies, bends and distorts the path of light from more distant objects.
- These are just a few examples of how the parabola formula is applied in various fields. Its versatile and widely recognized shape makes it a fundamental concept with broad utility.
| Related Links | |
| Fibonacci Sequence Formula | Eulers Formula |
| Exponential Formula | Factorial Formula |
Parabola Formula FAQs
Q1. What is a parabola?
Q2. What are the key elements of a parabola?
Q3. What is the focal length of a parabola?
Q4. How are parabolas used in real life?










