The
Perimeter of a Rectangle
formula signifies the complete distance encompassing its outer boundary. This measure is twice the sum of its length and width, and its computation is facilitated by the formula: Perimeter = 2(length + width).
What is the Perimeter of a Rectangle?
The perimeter of a rectangle refers to the cumulative length or distance tracing its boundary on all sides. It holds a linear dimension and is quantified in linear units such as meters, feet, inches, or yards. Let's delve into the two fundamental properties of a rectangle.
-
All four angles of a rectangle are 90°.
-
The opposing sides of a rectangle possess equal measures.
Imagine a rectangular park within your vicinity. Have you ever pondered over the length of its boundary?
Perimeter:
The Aggregate Length of a Rectangle's Boundary
When you traverse along the park's boundary once, you cover a specific distance. This distance constitutes the park's perimeter. To measure the perimeter of any rectangular area, you journey along its four sides, beginning at a fixed point and concluding at the same point. This distance or length of the boundary defines the rectangle's perimeter
Perimeter of Rectangle Formula
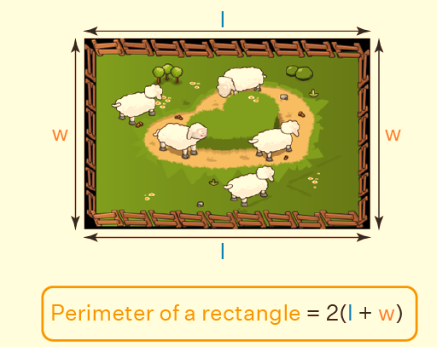
The mathematical expression employed to compute the perimeter of a rectangle is defined by the formula: perimeter of a rectangle = 2(l + w), where 'l' symbolizes the length, and 'w' represents the width of the rectangle. To illustrate the concept, consider an illustrative scenario involving David's intention to enclose his farm with a fence, preventing his sheep from wandering away. This formula can be better comprehended through a practical example, as described below. David seeks to ascertain the amount of wire needed to enclose his rectangular farm with a fence.
To facilitate understanding, let's assign designations to the sides of David's farm. The elongated side of this rectangular expanse is designated as 'l', while the shorter side is labelled as 'w'. When we sum the distances of all four sides of his farm, the cumulative length of the boundary is revealed. In mathematical terms, Total distance = l + w + l + w = 2l + 2w. Consequently, the Perimeter of a rectangle = 2(l + w). This formula can be effectively employed in the subsequent examples.
Examples Using Perimeter of Rectangle Formula
Example 1:
Determine the perimeter of a rectangle with sides measuring 12 cm and 8 cm.
Solution:
Employ the perimeter of a rectangle formula, Perimeter of rectangle = 2(l + w). Given the length (l) of the rectangle is 12 cm and the width (w) is 8 cm:
Upon substituting the values into the formula: Perimeter of rectangle = 2(l + w) = 2(12 + 8) = 2 × 20 = 40 cm. Hence, the rectangle's perimeter is 40 cm.
Example 2:
Calculate the perimeter of a rectangle with a length of 15 m and a width of 9 m.
Solution:
Given Length = 15 m; Width = 9 m. Utilizing the Perimeter of rectangle formula: P = 2(l + w) = 2(15 + 9) = 2 × 24 = 48 m. Thus, the rectangle's perimeter is 48 m.
Also Check –
Line and Angles Formula
Perimeter of Rectangle Formula vs. Perimeter of Square Formula
The formulas for rectangle perimeter and square perimeter differ:
-
The perimeter of the rectangle formula: Perimeter of rectangle = 2(l + w), with 'l' as length and 'w' as width. Conversely, the perimeter of a square formula: perimeter of a square = 4 × s, with 's' as side length.
-
The distinction arises because only the opposite sides of a rectangle are equal, while a square boasts all sides of equal length
Relationship Between Area and Perimeter of a Rectangle
The relationship between the rectangle area and perimeter is not direct. The perimeter is the cumulative length of its boundary, measured in linear units (cm, inches, etc.). The perimeter of a rectangle formula = 2(length + width). Conversely, the rectangle's area signifies the total occupied space and is measured in square units (cm², inches², etc.). The formula for rectangle area is Area = length × width.
Also Check –
Introduction to Graph Formula
How to Find the Perimeter of a Rectangle?
Three simple steps are involved in calculating a rectangle's perimeter:
-
Know the length and width of the rectangle.
-
Substitute the corresponding values into the formula.
-
Solve the equation to compute the perimeter.
The formula for calculating the perimeter of a rectangle is:
Perimeter of a rectangle = 2(l + w), where 'l' is the length, and 'w' is the width of the rectangle
We know that the formula used to calculate the perimeter of a rectangle is:
In scenarios where the perimeter is known and one dimension is missing:
If the perimeter and length are known, the width can be calculated using: Width = P/2 - l, where l = length, w = width, and P = perimeter.
Similarly, if the perimeter and width are known, the length can be calculated using: Length(L) = P/2 - w, where P = perimeter and w = width.
Usage of Perimeter of a Rectangle
-
The rectangle's perimeter simplifies calculations related to distances and lengths in our daily activities:
-
Decorate your notebook's edge: Compute the required ribbon length using the perimeter calculation.
-
Fence your garden: Determine the precise wire length based on the garden's perimeter.
Also Check –
Solid Shapes Formula
The Perimeter of Rectangle Examples
Example 1:
Let's consider bedsheets with a length of 120 inches and a width of 85 inches. What quantity of lace will be necessary to adorn its borders?
Solution:
To determine the lace required for the bedsheets' border, we'll calculate the perimeter of the bedsheets using the perimeter of a rectangle formula. Given: length = 120 inches, width = 85 inches. The formula for the perimeter of a rectangle is 2(l + w). Substituting the provided length and width values, we have Perimeter = 2(l + w) = 2(120 + 85) = 2 × 205 = 410 inches.
Hence, a total of 410 inches of lace is needed to embellish the border of the bedsheets.
Example 2:
Imagine your beloved chocolate bar consists of identical squares, each with a side measuring 1 inch. Compute the perimeter of this rectangular chocolate bar.
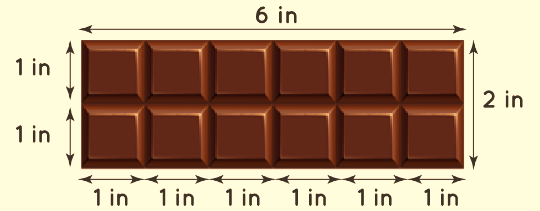
Solution:
Each small square within the chocolate bar has sides of 1 inch. By adding the sides of the squares along the bar's length, we obtain a sum of 6 inches. Similarly, summing the sides of the squares along the width yields 2 inches. Consequently, the length of the bar is 6 inches, and the width is 2 inches. Applying these measurements to the perimeter of a rectangle formula:
Perimeter = 2(l + w) = 2 (6 + 2) = 2 × 8 = 16 inches
Hence, the perimeter of the chocolate bar is 16 inches.
Example 3:
Let's determine the perimeter of a rectangle having a length of 15 mm and a width of 13 mm.
Solution:
Employing the perimeter of a rectangle formula, we can calculate its perimeter. Given: length (l) = 15 mm; width (w) = 13 mm.
Perimeter of rectangle = 2(l + w). Substituting these values into the formula: 2(l + w) = 2(15 + 13) = 2 × 28 = 56 mm.
Hence, the perimeter of the rectangle amounts to 56 mm.
