RD Sharma Solutions Class 10 Maths Chapter 5 Exercise 5.1 Trigonometric Ratios
RD Sharma Solutions Class 10 Maths Chapter 5 Exercise 5.1 Trigonometric Ratios has been provided here. Students can refer to these questions before their examinations for better preparation.
Neha Tanna7 Nov, 2024
Share
RD Sharma Solutions Class 10 Maths Chapter 5 Exercise 5.1: Chapter 5 of RD Sharma’s Class 10 Maths focuses on Trigonometric Ratios , introducing students to fundamental trigonometric concepts based on right-angled triangles. Exercise 5.1 specifically covers the basic trigonometric ratios - sine, cosine, tangent, cotangent, secant, and cosecant—defined as ratios of various sides of a right triangle (opposite, adjacent, and hypotenuse).
This exercise teaches students how to use these ratios to relate angles to side lengths, laying the groundwork for solving more complex trigonometric problems. It also involves understanding reciprocal relationships between ratios and solving questions to build confidence in applying these concepts effectively.RD Sharma Solutions Class 10 Maths Chapter 5 Exercise 5.1 Overview
Chapter 5, Exercise 5.1 in RD Sharma’s Class 10 Maths covers the basics of trigonometric ratios, focusing on fundamental concepts like sine, cosine, and tangent functions based on right-angled triangles. This exercise is crucial because understanding trigonometric ratios is foundational for higher-level mathematics, including calculus, geometry, and physics. By practicing these problems, students learn how to relate angles to side lengths, allowing them to solve real-life applications involving heights, distances, and angles. Mastery of these concepts strengthens analytical thinking and problem-solving skills, setting a solid base for advanced trigonometry and various applications in science and engineering.RD Sharma Solutions Class 10 Maths Chapter 5 Exercise 5.1 PDF
Below, we have provided the PDF solutions for RD Sharma Class 10 Maths, Chapter 5, Exercise 5.1, covering Trigonometric Ratios. This exercise focuses on introducing trigonometric ratios such as sine, cosine, and tangent, and their applications in solving various problems. These solutions will guide you through step-by-step methods to help understand the basics of trigonometry, making it easier to tackle more complex questions in later exercises. Download the PDF to enhance your learning.RD Sharma Solutions Class 10 Maths Chapter 5 Exercise 5.1 PDF
RD Sharma Solutions Class 10 Maths Chapter 5 Exercise 5.1 Trigonometric Ratios
Below is the RD Sharma Solutions Class 10 Maths Chapter 5 Exercise 5.1 Trigonometric Ratios -1. In each of the following, one of the six trigonometric ratios s given. Find the values of the other trigonometric ratios.
(i) sin A = 2/3
Solution:
We have, sin A = 2/3 ……..….. (1) As we know, by sin definition, sin A = Perpendicular/ Hypotenuse = 2/3 ….(2) By comparing eq. (1) and (2), we have Opposite side = 2 and Hypotenuse = 3 Now, on using Pythagoras theorem in Δ ABC AC 2 = AB 2 + BC 2 Putting the values of perpendicular side (BC) and hypotenuse (AC) and for the base side as (AB), we get ⇒ 3 2 = AB 2 + 2 2 AB 2 = 3 2 – 2 2 AB 2 = 9 – 4 AB 2 = 5 AB = √5 Hence, Base = √5 By definition, cos A = Base/Hypotenuse ⇒ cos A = √5/3 Since, cosec A = 1/sin A = Hypotenuse/Perpendicular ⇒ cosec A = 3/2 And, sec A = Hypotenuse/Base ⇒ sec A = 3/√5 And, tan A = Perpendicular/Base ⇒ tan A = 2/√5 And, cot A = 1/ tan A = Base/Perpendicular ⇒ cot A = √5/2(ii) cos A = 4/5
Solution:
We have, cos A = 4/5 …….…. (1) As we know, by cos definition, cos A = Base/Hypotenuse …. (2) By comparing eq. (1) and (2), we get Base = 4 and Hypotenuse = 5 Now, using Pythagoras’ theorem in Δ ABC, AC 2 = AB 2 + BC 2 Putting the value of base (AB) and hypotenuse (AC) and for the perpendicular (BC), we get 5 2 = 4 2 + BC 2 BC 2 = 5 2 – 4 2 BC 2 = 25 – 16 BC 2 = 9 BC= 3 Hence, Perpendicular = 3 By definition, sin A = Perpendicular/Hypotenuse ⇒ sin A = 3/5 Then, cosec A = 1/sin A ⇒ cosec A= 1/ (3/5) = 5/3 = Hypotenuse/Perpendicular And, sec A = 1/cos A ⇒ sec A =Hypotenuse/Base sec A = 5/4 And, tan A = Perpendicular/Base ⇒ tan A = 3/4 Next, cot A = 1/tan A = Base/Perpendicular ∴ cot A = 4/3(iii) tan θ = 11/1
Solution:
We have, tan θ = 11…..…. (1) By definition, tan θ = Perpendicular/ Base…. (2) On Comparing eq. (1) and (2), we get; Base = 1 and Perpendicular = 5 Now, using Pythagoras’ theorem in Δ ABC, AC 2 = AB 2 + BC 2 Putting the value of base (AB) and perpendicular (BC) to get hypotenuse(AC), we get AC 2 = 1 2 + 11 2 AC 2 = 1 + 121 AC 2 = 122 AC= √122 Hence, hypotenuse = √122 By definition, sin = Perpendicular/Hypotenuse ⇒ sin θ = 11/√122 And, cosec θ = 1/sin θ ⇒ cosec θ = √122/11 Next, cos θ = Base/ Hypotenuse ⇒ cos θ = 1/√122 And, sec θ = 1/cos θ ⇒ sec θ = √122/1 = √122 And, cot θ = 1/tan θ ∴ cot θ = 1/11(iv) sin θ = 11/15
Solution:
We have, sin θ = 11/15 ………. (1) By definition, sin θ = Perpendicular/ Hypotenuse …. (2) On Comparing eq. (1) and (2), we get, Perpendicular = 11 and Hypotenuse= 15 Now, using Pythagoras’ theorem in Δ ABC, AC 2 = AB 2 + BC 2 Putting the value of perpendicular (BC) and hypotenuse (AC) to get the base (AB), we have 15 2 = AB 2 +11 2 AB 2 = 15 2 – 11 2 AB 2 = 225 – 121 AB 2 = 104 AB = √104 AB= √ (2×2×2×13) AB= 2√(2×13) AB= 2√26 Hence, Base = 2√26 By definition, cos θ = Base/Hypotenuse ∴ cosθ = 2√26/ 15 And, cosec θ = 1/sin θ ∴ cosec θ = 15/11 And, secθ = Hypotenuse/Base ∴ secθ =15/ 2√26 And, tan θ = Perpendicular/Base ∴ tanθ =11/ 2√26 And, cot θ = Base/Perpendicular ∴ cotθ =2√26/ 11(v) tan α = 5/12
Solution:
We have, tan α = 5/12 …. (1) By definition, tan α = Perpendicular/Base…. (2) On Comparing eq. (1) and (2), we get Base = 12 and Perpendicular side = 5 Now, using Pythagoras’ theorem in Δ ABC, AC 2 = AB 2 + BC 2 Putting the value of base (AB) and the perpendicular (BC) to get hypotenuse (AC), we have AC 2 = 12 2 + 5 2 AC 2 = 144 + 25 AC 2 = 169 AC = 13 [After taking sq root on both sides] Hence, Hypotenuse = 13 By definition, sin α = Perpendicular/Hypotenuse ∴ sin α = 5/13 And, cosec α = Hypotenuse/Perpendicular ∴ cosec α = 13/5 And, cos α = Base/Hypotenuse ∴ cos α = 12/13 And, sec α =1/cos α ∴ sec α = 13/12 And, tan α = sin α/cos α ∴ tan α=5/12 Since, cot α = 1/tan α ∴ cot α =12/5(vi) sin θ = √3/2
Solution:
We have, sin θ = √3/2 …………. (1) By definition, sin θ = Perpendicular/ Hypotenuse….(2) On Comparing eq. (1) and (2), we get Perpendicular = √3 and Hypotenuse = 2 Now, using Pythagoras’ theorem in Δ ABC, AC 2 = AB 2 + BC 2 Putting the value of perpendicular (BC) and hypotenuse (AC) and get the base (AB), we get 2 2 = AB 2 + (√3) 2 AB 2 = 2 2 – (√3) 2 AB 2 = 4 – 3 AB 2 = 1 AB = 1 Thus, Base = 1 By definition, cos θ = Base/Hypotenuse ∴ cos θ = 1/2 And, cosec θ = 1/sin θ Or cosec θ= Hypotenuse/Perpendicualar ∴ cosec θ =2/√3 And, sec θ = Hypotenuse/Base ∴ sec θ = 2/1 And, tan θ = Perpendicula/Base ∴ tan θ = √3/1 And, cot θ = Base/Perpendicular ∴ cot θ = 1/√3(vii) cos θ = 7/25
Solution:
We have, cos θ = 7/25 ……….. (1) By definition, cos θ = Base/Hypotenuse On Comparing eq. (1) and (2), we get; Base = 7 and Hypotenuse = 25 Now, using Pythagoras’ theorem in Δ ABC, AC 2 = AB 2 + BC 2 Putting the value of base (AB) and hypotenuse (AC) to get the perpendicular (BC), 25 2 = 7 2 +BC 2 BC 2 = 25 2 – 7 2 BC 2 = 625 – 49 BC 2 = 576 BC= √576 BC= 24 Hence, Perpendicular side = 24 By definition, sin θ = perpendicular/Hypotenuse ∴ sin θ = 24/25 Since, cosec θ = 1/sin θ Also, cosec θ= Hypotenuse/Perpendicualar ∴ cosec θ = 25/24 Since, sec θ = 1/cosec θ Also, sec θ = Hypotenuse/Base ∴ sec θ = 25/7 Since, tan θ = Perpendicular/Base ∴ tan θ = 24/7 Now, cot = 1/tan θ So, cot θ = Base/Perpendicular ∴ cot θ = 7/24(viii) tan θ = 8/15
Solution:
We have, tan θ = 8/15 …………. (1) By definition, tan θ = Perpendicular/Base …. (2) On Comparing eq. (1) and (2), we get Base = 15 and Perpendicular = 8 Now, using Pythagoras’ theorem in Δ ABC, AC 2 = 15 2 + 8 2 AC 2 = 225 + 64 AC 2 = 289 AC = √289 AC = 17 Hence, Hypotenuse = 17 By definition, Since, sin θ = perpendicular/Hypotenuse ∴ sin θ = 8/17 Since, cosec θ = 1/sin θ Also, cosec θ = Hypotenuse/Perpendicular ∴ cosec θ = 17/8 Since, cos θ = Base/Hypotenuse ∴ cos θ = 15/17 Since, sec θ = 1/cos θ Also, sec θ = Hypotenuse/Base ∴ sec θ = 17/15 Since, cot θ = 1/tan θ Also, cot θ = Base/Perpendicular ∴ cot θ = 15/8(ix) cot θ = 12/5
Solution:
We have, cot θ = 12/5 …………. (1) By definition, cot θ = 1/tan θ cot θ = Base/Perpendicular ……. (2) On Comparing eq. (1) and (2), we have Base = 12 and Perpendicular side = 5 Now, using Pythagoras’ theorem in Δ ABC, AC 2 = AB 2 + BC 2 Putting the value of base (AB) and perpendicular (BC) to get the hypotenuse (AC), AC 2 = 12 2 + 5 2 AC 2 = 144 + 25 AC 2 = 169 AC = √169 AC = 13 Hence, Hypotenuse = 13 By definition, Since, sin θ = perpendicular/Hypotenuse ∴ sin θ= 5/13 Since, cosec θ = 1/sin θ Also, cosec θ= Hypotenuse/Perpendicualar ∴ cosec θ = 13/5 Since, cos θ = Base/Hypotenuse ∴ cos θ = 12/13 Since, sec θ = 1/cosθ Also, sec θ = Hypotenuse/Base ∴ sec θ = 13/12 Since, tanθ = 1/cot θ Also, tan θ = Perpendicular/Base ∴ tan θ = 5/12(x) sec θ = 13/5
Solution:
We have, sec θ = 13/5…….… (1) By definition, sec θ = Hypotenuse/Base…………. (2) On Comparing eq. (1) and (2), we get Base = 5 and Hypotenuse = 13 Now, using Pythagoras’ theorem in Δ ABC, AC 2 = AB 2 + BC 2 And putting the value of base side (AB) and hypotenuse (AC) to get the perpendicular side (BC), 13 2 = 5 2 + BC 2 BC 2 = 13 2 – 5 2 BC 2 =169 – 25 BC 2 = 144 BC= √144 BC = 12 Hence, Perpendicular = 12 By definition, Since, sin θ = perpendicular/Hypotenuse ∴ sin θ= 12/13 Since, cosec θ= 1/ sin θ Also, cosec θ= Hypotenuse/Perpendicular ∴ cosec θ = 13/12 Since, cos θ= 1/sec θ Also, cos θ = Base/Hypotenuse ∴ cos θ = 5/13 Since, tan θ = Perpendicular/Base ∴ tan θ = 12/5 Since, cot θ = 1/tan θ Also, cot θ = Base/Perpendicular ∴ cot θ = 5/12(xi) cosec θ = √10
Solution:
We have, cosec θ = √10/1 ……..… (1) By definition, cosec θ = Hypotenuse/ Perpendicualar …….….(2) And, cosecθ = 1/sin θ On comparing eq.(1) and(2), we get Perpendicular side = 1 and Hypotenuse = √10 Now, using Pythagoras’ theorem in Δ ABC, AC 2 = AB 2 + BC 2 Putting the value of perpendicular (BC) and hypotenuse (AC) to get the base side (AB), (√10) 2 = AB 2 + 1 2 AB 2 = (√10) 2 – 1 2 AB 2 = 10 – 1 AB = √9 AB = 3 So, Base side = 3 By definition, Since, sin θ = Perpendicular/Hypotenuse ∴ sin θ = 1/√10 Since, cos θ = Base/Hypotenuse ∴ cos θ = 3/√10 Since, sec θ = 1/cos θ Also, sec θ = Hypotenuse/Base ∴ sec θ = √10/3 Since, tan θ = Perpendicular/Base ∴ tan θ = 1/3 Since, cot θ = 1/tan θ ∴ cot θ = 3/1(xii) cos θ =12/15
Solution:
We have; cos θ = 12/15 ………. (1) By definition, cos θ = Base/Hypotenuse……… (2) By comparing eq. (1) and (2), we get; Base =12 and Hypotenuse = 15 Now, using Pythagoras’ theorem in Δ ABC, we get AC 2 = AB 2 + BC 2 Putting the value of base (AB) and hypotenuse (AC) to get the perpendicular (BC), 15 2 = 12 2 + BC 2 BC 2 = 15 2 – 12 2 BC 2 = 225 – 144 BC 2 = 81 BC = √81 BC = 9 So, Perpendicular = 9 By definition, Since, sin θ = perpendicular/Hypotenuse ∴ sin θ = 9/15 = 3/5 Since, cosec θ = 1/sin θ Also, cosec θ = Hypotenuse/Perpendicular ∴ cosec θ= 15/9 = 5/3 Since, sec θ = 1/cos θ Also, sec θ = Hypotenuse/Base ∴ sec θ = 15/12 = 5/4 Since, tan θ = Perpendicular/Base ∴ tan θ = 9/12 = 3/4 Since, cot θ = 1/tan θ Also, cot θ = Base/Perpendicular ∴ cot θ = 12/9 = 4/32. In a △ ABC, right-angled at B, AB = 24 cm , BC = 7 cm. Determine
(i) sin A , cos A (ii) sin C, cos C
Solution:
(i) Given: In △ABC, AB = 24 cm, BC = 7cm and ∠ABC = 90 o
To find: sin A, cos A By using Pythagoras’ theorem in △ABC, we have AC 2 = AB 2 + BC 2 AC 2 = 24 2 + 7 2 AC 2 = 576 + 49 AC 2 = 625 AC = √625 AC= 25 Hence, Hypotenuse = 25 By definition, sin A = Perpendicular side opposite to angle A/ Hypotenuse sin A = BC/ AC sin A = 7/ 25 And, cos A = Base side adjacent to angle A/Hypotenuse cos A = AB/ AC cos A = 24/ 25
(ii) Given: In △ABC , AB = 24 cm and BC = 7cm and ∠ABC = 90 o
To find: sin C, cos C By using Pythagoras’ theorem in △ABC, we have AC 2 = AB 2 + BC 2 AC 2 = 24 2 + 7 2 AC 2 = 576 + 49 AC 2 = 625 AC = √625 AC= 25 Hence, Hypotenuse = 25 By definition, sin C = Perpendicular side opposite to angle C/Hypotenuse sin C = AB/ AC sin C = 24/ 25 And, cos C = Base side adjacent to angle C/Hypotenuse cos A = BC/AC cos A = 7/253. In fig. 5.37, find tan P and cot R. Is tan P = cot R?
Solution:
Yes, tan P = cot R = 5/12
4. If sin A = 9/41, compute cos A and tan A.
Solution:
5. Given 15cot A= 8, find sin A and sec A.
Solution
We have, 15cot A = 8
Required to find: sin A and sec A
As, 15 cot A = 8
⇒ cot A = 8/15 …….(1)
And we know,
cot A = 1/tan A
Also by definition,
Cot A = Base side adjacent to ∠A/ Perpendicular side opposite to ∠A …. (2)
On comparing equation (1) and (2), we get
Base side adjacent to ∠A = 8
Perpendicular side opposite to ∠A = 15
So, by using Pythagoras theorem to △ABC, we have
AC
2
= AB
2
+BC
2
Substituting values for sides from the figure
AC
2
= 8
2
+ 15
2
AC
2
= 64 + 225
AC
2
= 289
AC = √289
AC = 17
Therefore, hypotenuse =17
By definition,
sin A = Perpendicular/Hypotenuse
⇒ sin A= BC/AC
sin A= 15/17 (using values from the above)
Also,
sec A= 1/ cos A
⇒ secA = Hypotenuse/ Base side adjacent to ∠A
∴ sec A= 17/8
6. In △PQR, right-angled at Q, PQ = 4cm and RQ = 3 cm. Find the value of sin P, sin R, sec P and sec R.
Solution:
7. If cot θ = 7/8, evaluate
(i) (1+sin θ)(1–sin θ)/ (1+cos θ)(1–cos θ)
(ii) cot 2 θ
Solution:
(i) Required to evaluate:
, given = cot θ = 7/8
Taking the numerator, we have
(1+sin θ)(1–sin θ) = 1 – sin
2
θ [Since, (a+b)(a-b) = a
2
– b
2
]
Similarly,
(1+cos θ)(1–cos θ) = 1 – cos
2
θ
We know that,
sin
2
θ + cos
2
θ = 1
⇒ 1 – cos
2
θ = sin
2
θ
And,
1 – sin
2
θ = cos
2
θ
Thus,
(1+sin θ)(1 –sin θ) = 1 – sin
2
θ = cos
2
θ
(1+cos θ)(1–cos θ) = 1 – cos
2
θ = sin
2
θ
⇒
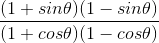= cos
2
θ/ sin
2
θ
= (cos θ/sin θ)
2
And, we know that (cos θ/sin θ) = cot θ
⇒
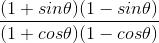
= (cot θ) 2
= (7/8) 2 = 49/ 64(ii) Given,
cot θ = 7/8 So, by squaring on both sides we get (cot θ) 2 = (7/8) 2 ∴ cot θ 2 = 49/648. If 3cot A = 4, check whether (1–tan 2 A)/(1+tan 2 A) = (cos 2 A – sin 2 A) or not.
Solution:
Thus, LHS = 7/25
Now, taking RHS,
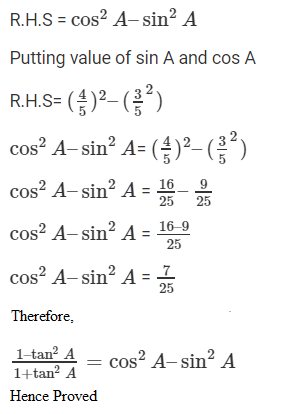
9. If tan θ = a/b, find the value of (cos θ + sin θ)/ (cos θ – sin θ)
Solution:
Given, tan θ = a/b And we know by definition that tan θ = opposite side/ adjacent side Thus, by comparison, Opposite side = a and adjacent side = b To find the hypotenuse, we know that by Pythagoras theorem that Hypotenuse 2 = opposite side 2 + adjacent side 2 ⇒ Hypotenuse = √(a 2 + b 2 ) So, by definition sin θ = opposite side/ Hypotenuse sin θ = a/ √(a 2 + b 2 ) And, cos θ = adjacent side/ Hypotenuse cos θ = b/ √(a 2 + b 2 ) Now, After substituting for cos θ and sin θ, we have
∴
Hence, proved.
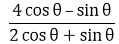
10. If 3 tan θ = 4, find the value of
Solution:
Given, 3 tan θ = 4 ⇒ tan θ = 4/3
From, let’s divide the numerator and denominator by cos θ.
We get,
(4 – tan θ) / (2 + tan θ)
⇒ (4 – (4/3)) / (2 + (4/3)) [using the value of tan θ]
⇒ (12 – 4) / (6 + 4) [After taking LCM and cancelling it]
⇒ 8/10 = 4/5
∴ = 4/5
11. If 3 cot θ = 2, find the value of
Solution:
Given, 3 cot θ = 2 ⇒ cot θ = 2/3
From, let’s divide the numerator and denominator by sin θ.
We get,
(4 –3 cot θ) / (2 + 6 cot θ)
⇒ (4 – 3(2/3)) / (2 + 6(2/3)) [using the value of tan θ]
⇒ (4 – 2) / (2 + 4) [After taking LCM and simplifying it]
⇒ 2/6 = 1/3
∴ = 1/3
12. If tan θ = a/b, prove that
Solution:
Given, tan θ = a/b
From LHS, let’s divide the numerator and denominator by cos θ.
And we get,
(a tan θ – b) / (a tan θ + b)
⇒ (a(a/b) – b) / (a(a/b) + b) [using the value of tan θ]
⇒ (a
2
– b
2
)/b
2
/ (a
2
+ b
2
)/b
2
[After taking LCM and simplifying it]
⇒ (a
2
– b
2
)/ (a
2
+ b
2
)
= RHS
Hence, proved
13. If sec θ = 13/5, show that
Solution:
From, let’s divide the numerator and denominator by cos θ.
We get,
(2 tan θ – 3) / (4 tan θ – 9)
⇒ (2(12/5) – 3) / (4(12/5) – 9) [using the value of tan θ]
⇒ (24 – 15) / (48 – 45) [After taking LCM and cancelling it]
⇒ 9/3 = 3
∴ = 3
14. If cos θ = 12/13, show that sin θ(1 – tan θ) = 35/156
Solution:
Given, cos θ = 12/13…… (1)
By definition, we know that
cos θ = Base side adjacent to ∠θ / Hypotenuse……. (2)
When comparing equation (1) and (2), we get
Base side adjacent to ∠θ = 12 and Hypotenuse = 13
From the figure,
Base side BC = 12
Hypotenuse AC = 13
Side AB is unknown here, and it can be found by using Pythagoras theorem.
Thus, by applying Pythagoras theorem,
AC
2
= AB
2
+ BC
2
13
2
= AB
2
+ 12
2
Therefore,
AB
2
= 13
2
– 12
2
AB
2
= 169 – 144
AB
2
= 25
AB = √25
AB = 5 …. (3)
Now, we know that
sin θ = Perpendicular side opposite to ∠θ / Hypotenuse
Thus, sin θ = AB/AC [from figure]
⇒ sin θ = 5/13… (4)
And, tan θ = sin θ / cos θ = (5/13) / (12/13)
⇒ tan θ = 12/13… (5)
Taking L.H.S we have
L.H.S = sin θ (1 – tan θ)
Substituting the value of sin θ and tan θ from equation (4) and (5),
We get,
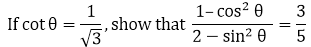
15.
Solution:
Given, cot θ = 1/
√
3……. (1)
By definition, we know that,
cot θ = 1/ tan θ
And, since tan θ = perpendicular side opposite to ∠θ / Base side adjacent to ∠θ
⇒ cot θ = Base side adjacent to ∠θ / perpendicular side opposite to ∠θ …… (2)
[Since they are reciprocal to each other]
On comparing equation (1) and (2), we get
Base side adjacent to ∠θ = 1 and Perpendicular side opposite to ∠θ = √3
Therefore, the triangle formed is
On substituting the values of known sides as AB = √3 and BC = 1,
AC
2
= (√3) + 1
AC
2
= 3 + 1
AC
2
= 4
AC = √4
Therefore, AC = 2 … (3)
Now, by definition,
sin θ = Perpendicular side opposite to ∠θ / Hypotenuse = AB / AC
⇒ sin θ = √3/ 2 ……(4)
And, cos θ = Base side adjacent to ∠θ / Hypotenuse = BC / AC
⇒ cos θ = 1/ 2 ….. (5)
Now, taking L.H.S, we have
Substituting the values from equation (4) and (5), we have
16.
Solution:
Given, tan θ = 1/ √7 …..(1)
Substituting the value of cosec θ and sec θ from equation (3) and (4), we get
17. If sec θ = 5/4, find the value of
Solution:
Given, sec θ = 5/4 We know that, sec θ = 1/ cos θ ⇒ cos θ = 1/ (5/4) = 4/5 …… (1) By definition, cos θ = Base side adjacent to ∠θ / Hypotenuse …. (2) On comparing equation (1) and (2), we have Hypotenuse = 5 Base side adjacent to ∠θ = 4 Thus, the triangle representing ∠ θ is ABC. Perpendicular side opposite to ∠θ, AB is unknown, and it can be found by using Pythagoras theorem. By applying Pythagoras’ theorem, we have AC 2 = AB 2 + BC 2 AB 2 = AC 2 + BC 2 AB 2 = 5 2 – 4 2 AB 2 = 25 – 16 AB = √9 ⇒ AB = 3 By definition, sin θ = Perpendicular side opposite to ∠θ / Hypotenuse = AB / AC ⇒ sin θ = 3/ 5 …..(3) Now, tan θ = Perpendicular side opposite to ∠θ / Base side adjacent to ∠θ ⇒ tan θ = 3/ 4 ……(4) And, since cot θ = 1/ tan θ ⇒ cot θ = 4/ 3 ……(5) Now, Substituting the value of sin θ, cos θ, cot θ and tan θ from the equations (1), (3), (4) and (5), we have
= 12/7
Therefore,
18. If tan θ = 12/13, find the value of
Solution:
Given, tan θ = 12/13 …….. (1) We know that by definition, tan θ = Perpendicular side opposite to ∠θ / Base side adjacent to ∠θ …… (2) On comparing equation (1) and (2), we have The perpendicular side opposite to ∠θ = 12 Base side adjacent to ∠θ = 13 Thus, in the triangle representing ∠ θ, we have, Hypotenuse AC is the unknown, and it can be found by using Pythagoras theorem. So, by applying Pythagoras’ theorem, we have AC 2 = 12 2 + 13 2 AC 2 = 144 + 169 AC 2 = 313 ⇒ AC = √313 By definition, sin θ = Perpendicular side opposite to ∠θ / Hypotenuse = AB / AC ⇒ sin θ = 12/ √313…..(3) And, cos θ = Base side adjacent to ∠θ / Hypotenuse = BC / AC ⇒ cos θ = 13/ √313 …..(4) Now, substituting the value of sin θ and cos θ from equation (3) and (4), respectively, in the equation below,
Therefore,
Benefits of Solving RD Sharma Solutions Class 10 Maths Chapter 5 Exercise 5.1
Solving RD Sharma Solutions for Class 10 Maths Chapter 5, Exercise 5.1 on Trigonometric Ratios offers several benefits:Strong Foundation in Trigonometry : Exercise 5.1 introduces students to basic trigonometric ratios like sine, cosine, tangent, and their reciprocals. Practicing this helps build a solid foundation for more advanced concepts in trigonometry.
Enhanced Problem-Solving Skills : Working through RD Sharma's exercises encourages a step-by-step approach to solving problems, which improves analytical thinking and problem-solving skills.
Understanding Real-Life Applications : Trigonometry is widely used in fields like physics, engineering, architecture, and astronomy. By mastering the basics, students can better understand these applications.
Preparation for Competitive Exams : The exercises in RD Sharma's book are similar to those in competitive exams, providing students with a strong base for exams that require trigonometric knowledge.
Concept Clarity : Detailed solutions and explanations aid in clearing any doubts regarding trigonometric concepts, making it easier to retain and apply them in higher classes.
RD Sharma Solutions Class 10 Maths Chapter 5 Exercise 5.1 FAQs
What is the purpose of trigonometric ratios?
Trigonometric ratios can be used to determine the ratios of any two sides out of a total of three sides of a right-angled triangle in terms of the respective angles.
How are trigonometric ratios derived?
Trigonometric Ratios are defined as the values of all the trigonometric functions based on the value of the ratio of sides in a right-angled triangle. The ratios of sides of a right-angled triangle with respect to any of its acute angles are known as the trigonometric ratios of that particular angle.
What are the most important trigonometric ratios?
Trigonometric ratios relate the ratio of sides of a right triangle to the respective angle in trigonometry. The basic trigonometric ratios used in trigonometry are sin, cos, and tan, namely, sine, cosine, and tangent. Other important trigonometric ratios are cosec, sec, and cot, derived from sin, cos, and tan.
What is the relationship between trigonometric ratios?
Reciprocal Relationship
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App
