
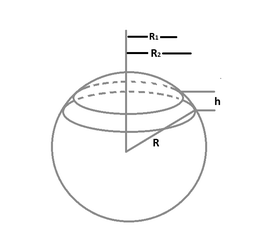
Spherical Segment Formula: A spherical segment is like a slice taken from the top and bottom of a ball with a flat, parallel cut. It looks similar to a rounded cap with the tip cut off. The zone refers to the surface of this slice, not including the top and bottom parts.
Spherical Segment Formulas
The formulas for a spherical segment consist of both its area and volume calculations. Here, we'll delve into the specific formulas for finding the area and volume of a spherical segment.
Area Formula for a Spherical Segment
The area of a spherical segment represents the space it covers within a three-dimensional context. It's calculated as the product of its radius and height, multiplied by a constant value of 2π.
Formula for the Area: A=2πrh
Where: r represents the segment's radius, h denotes the segment's height.
Volume of a Spherical Segment: The volume of a spherical segment denotes the space enclosed within it. It's computed as the product of the height and the sum of three times the square of the smaller radius, three times the square of the larger radius, and the square of the height, multiplied by a constant value of π/6.
V=πh(3R 1 2 +3R 2 2 +h 2 )/6
Where: R 1 signifies the radius of the smaller bounded region, R 2 represents the radius of the larger bounded region, h stands for the segment's height.
Spherical Segment Formula Solved Examples
Example 1: Determine the area of a segment of a sphere with a sphere radius of 10 cm and a height of 5 cm.
Solution: Given: R=10 and h=5.
Using the Spherical Segment Formula: A=2πRh
= 2 × ( 22 /7 ) × 10 × 5
=2×( 22/7 )×10×5
= 314 sq. cm
=314 sq. cm
Example 2: Find the height of a segment of a sphere if the sphere's radius is 12 cm and the area is 216 sq. cm.
Solution: Given: R=12 and A=216.
Using the Spherical Segment Formula: A=2πRh
216=2×( 22/7 )×12×h
h= 2.86 cm
Example 3: Calculate the volume of a segment of a sphere given a sphere radius of 15 cm, base radius of 8 cm, and a height of 6 cm.
Solution: Given: R 1 =15, R 2 =8, and h=6.
Using the Spherical Segment Formula: V=πh(3R 1 2 +3R 2 2 +h 2 )/6
= ( 22/ 7 ) × 6 × ( 3 × 1 5 2 + 3 × 8 2 + 6 2 ) / 6
= ( 22/ 7 ) × 6 × ( 675 + 192 + 36 ) / 6
= 2835.42 cu. cm
Example 4 : Find the volume of a segment of a sphere with a sphere radius of 20 cm, base radius of 14 cm, and a height of 8 cm.
Solution: Given: R 1 =20, R 2 =14, and h=8.
Using the formula: V=πh(3R 1 2 +3R 2 2 +h 2 )/6
= ( 22/ 7 ) × 8 × ( 3 × 2 0 2 + 3 × 1 4 2 + 8 2 ) / 6
=( 22/ 7 ) × 8 × ( 1200 + 588 + 64 ) / 6
=( 22/7 )×8×(1200+588+64)/6
= 7753.70 cu. cm
These examples demonstrate the application of formulas for finding the area and volume of spherical segments using given parameters.
Understanding and applying the formulas for the area and volume of spherical segments is essential in solving problems related to spheres in geometry and mathematics. The area of a spherical segment ( A) is determined by the product of the radius ( r) and the height ( h) multiplied by 2π, given by A=2πrh . This formula helps find the surface area covered by the segment.
The volume of a spherical segment ( V) relies on the heights and radii of the sphere and the segment's base. It's calculated as V=πh(3R 1 2 +3R 2 2 +h 2 )/6 , where R 1 and R 2 are the radii of the smaller and larger bounded regions, respectively.
Explore Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your Maths knowledge. and build a strong foundation.
| Related Links | |
| Hexagonal Pyramid Formula | Hypothesis Testing Formula |
| Interquartile Range Formula | Inverse Variation Formula |
Spherical Segment Formula FAQs
What is the formula for the area of a spherical segment?
How is the volume of a spherical segment calculated?
What does the area formula signify?
What does the volume formula represent?










