
Standard Form Formula: The standard form serves as the universally accepted method to represent various notations. In the field of equations, the standard form formula specifically embodies the commonly acknowledged structure of an equation. For instance, in polynomials, adhering to the standard form involves arranging terms in descending order of degree, with coefficients expressed as integers. Ultimately, this standard form formula facilitates a consistent and general representation across diverse notational contexts.
The formulation of the standard form revolves around the equations' degrees. It encompasses examining the standard representations of both basic linear equations and quadratic equations.
Standard Form Formula
Standard form of linear equation: ax+by = c
Standard form of a quadratic equation : ax 2 +bx+c = 0
Standard Form Expression The standard form of a linear equation serves as the fundamental structure for equations. It is depicted differently based on the number of variables involved. In the case of linear equations, variables like x, y, or (x) 1 , (x) 2 , (x) 3 ,... signify the variables, while a, b, (A) 1 , (A) 2 , (A) 3 ,...(A)n represent the coefficients.
The values placed to the right of the equals sign are termed as constants. For a linear equation with two variables: ax+by=c
For a linear equation with more than two variables:
(A) 1 (x) 1 +(A) 2 (x) 2 +(A) 3 (x) 3 +...+(A) n (x) n =D A quadratic equation, which is a second-degree equation with a single variable x, includes coefficients and a constant term, and is structured in the following manner:
ax 2 +bx+c=0 (Where a is not equal to zero)
Furthermore, standard form expressions exist for equations of higher degrees. In coordinate geometry, distinct standard forms are utilized to represent various geometric shapes such as lines, circles, ellipses, hyperbolas, and parabolas.
Straight Line: Ax+By=C,
where A is a positive integer, and B and C are integers.
Standard Form Formula Circle: (x−h) 2 +(y−k) 2 =r 2 , where (h,k) represents the center, and r denotes the radius.
Standard Form Formula Ellipse:
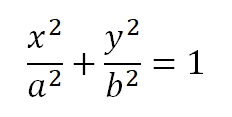
Hyperbola:
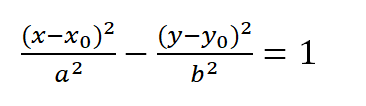
Where (x) 0 represents the center points, a denotes the semi-major axis, and b signifies the semi-minor axis.
Parabola: (x - h) 2 = 4p(y - k)
Standard Form Formula Solved Examples
Example 1: Converting the linear equation 4y−2x=8 into standard form.
Solution 4y−2x=8
4y=2x+8
y= 2x+8 /4
y= 1/2 x+2 (Simplified form)
2y=x+4 (Multiply both sides by 2 to eliminate fractions)
x−2y=−4 (Rearrange terms to get standard form)
Answer: The standard form of the given linear equation is x−2y=−4.
Example 2: Converting the quadratic equation x 2 +6x=−8 into standard form.
Solution:
x 2 +6x=−8
x 2 +6x+8=0 (Shifting constant to the other side)
x 2 +6x+9=1 (Completing the square by adding ( 6 / 2 ) 2 = 9 (6/2) 2 =9 to both sides)
(x+3) 2 =1 (Factorizing)
x+3=± 1
x+3=±1
x=−3±1
x=−2 or x=−4
Answer: The standard form of the given quadratic equation is x 2 +6x+8=0.
These examples demonstrate the process of transforming equations into their respective standard forms.
The concept of standard form serves as a crucial framework for expressing various equations in a universally accepted manner. Whether dealing with linear equations, quadratic equations, or higher-degree equations such as polynomials, adhering to the standard form involves organizing terms to establish a commonly acknowledged structure. The standard form, with coefficients as integers and terms arranged in a descending order of degree, allows for a consistent and general representation across diverse notational contexts.
Moreover, beyond the field of basic equations, the standard form extends its applicability to represent geometric shapes in coordinate geometry, including lines, circles, ellipses, hyperbolas, and parabolas, each with its distinctive formula.
The universal applicability and structured nature of standard form enable mathematicians and learners to comprehend and manipulate equations effectively, ensuring a standardized approach to mathematical representations.
Explore Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your Maths knowledge. and build a strong foundation.
| Related Links | |
| Tangent Line Formula | Tangent to a Circle Formula |
| Tangent 3 Theta Formula | Tan Theta Formula |
What is the standard form in mathematics?
How does one convert equations into standard form?
Why is standard form important in mathematics?
In what areas of mathematics is the standard form used?










