Sum to n Terms of Arithmetic Progression Formula: Definition, Examples
Sum to n Terms of Arithmetic Progression Formula: Summing the first 'n' terms in an Arithmetic Progression (AP) is done with the formula: Sn = n/2 [2a + (n-1)d], where 'a' represents the initial term, 'd' is the consistent difference, and 'n' stands for the quantity of terms.
Manoj Kumar16 Sept, 2023
Share
Sum to n Terms of Arithmetic Progression Formula: An arithmetic progression (AP) is a series of numbers where the gap between each pair of neighboring terms stays the same. This article explains how to calculate the total of the initial 'n' terms in an arithmetic progression using formulas and also delves into its historical background.
Also Check - Rational Number FormulaDefining the Sum of n Terms in an AP
In the 19th-century math class in Germany, where students were tasked with summing all numbers from 1 to 100. A young Carl Friedrich Gauss swiftly declared the answer as 5050, astonishing his peers. How did he achieve this feat?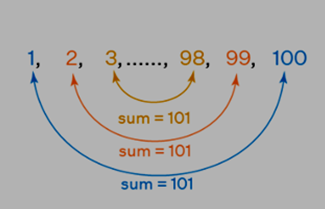
Gauss observed that terms equidistant from the series' beginning and end had a constant sum of 101. In the sequence 1, 2, 3, ..., 100, there are 50 such pairs, resulting in a total sum of 5050.
Also Check -
Linear Equation Formula
Sum to n Terms of Arithmetic Progression Formula
The sum of 'n' terms in an AP can be calculated using a straightforward formula: Sn = n/2 [2a + (n-1)d]. Here, 'a' represents the first term, 'd' is the common difference, and 'n' denotes the number of terms. In mathematical terms, for an AP presented as "a, a+d, a+2d, a+3d, ....., a+(n-1)d," the formula is expressed as: Sum = n/2 × [2a + (n-1)d] Also Check - Logarithm FormulaSum to n Terms of Arithmetic Progression Formula with the Last Term Known
If you possess knowledge of the last term 'an' in an arithmetic progression, you can use the formula: Sn = n/2 × [a1 + an] to determine the sum of the first 'n' terms. Here, 'a1' denotes the first term, and 'an' signifies the last term.Proof of the Sum to n Terms of Arithmetic Progression Formula
To validate the formula for the sum of 'n' terms in an AP, consider an AP with 'n' terms: a, a+d, a+2d,... (a+(n−2)d), (a+(n−1)d) The sum of 'n' terms in this progression can be expressed as: S n = a + (a+d) + … + (a+(n−2)d) + (a+(n−1)d) By rearranging the terms, we obtain: S n = (a+(n−1)d) + (a+(n−2)d) + … + (a+d) + a Summing corresponding terms from both equations yields the same result: 2a+(n−1)d. As there are 'n' terms in the AP, we can add both equations to derive: 2 S n = n(2a+(n−1)d) S n = n/2 (2a+(n−1)d)
This equation can also be expressed as:
Sn = n/2 (a1 + an)
Sum of an Infinite AP
Consider an infinite AP: 2 + 5 + 8 + ...
Here, the first term 'a' is 2, the common difference 'd' is 3, and the number of terms 'n' is ∞. Using the sum of an AP formula:
S
n
= n/2 (2a+(n−1)d)
S
n
= ∞/2 [2(2)+(∞−1)3]
S
n
= ∞
For a positive 'd,' the sum of an infinite AP is ∞, and for a negative 'd,' it is -∞.
Sum to n Terms of Arithmetic Progression Formula Solved Examples
Example 1: Finding the Sum of the First 10 Terms in an AP Given an arithmetic progression with the first term 'a' as 2 and the common difference 'd' as 3, calculate the sum of the first 10 terms Solution: Using the formula Sn = n/2 [2a + (n-1)d]: S n = 10/2 [2(2) + (10-1)(3)] S n = 5 [4 + 27] S n = 5 * 31 S n = 155 So, the sum of the first 10 terms in this AP is 155. Example 2: Finding the Sum of an AP When the Last Term is Known Given an AP with the first term 'a1' as 10, the last term 'an' as 70, and the number of terms 'n' as 8, calculate the sum of the first 8 terms. Solution: Using the formula Sn = n/2 [a1 + an]: Sn = 8/2 [10 + 70] S n = 4 [80] S n = 320 The sum of the first 8 terms in this AP is 320. Example 3: Sum of an Infinite AP Consider an infinite AP with the first term 'a' as 3 and a common difference 'd' of -2. Determine the sum of this infinite AP. Solution: Using the formula for an infinite AP: S n = ∞ when d < 0 So, in this case, the sum of the infinite AP is -∞. These examples demonstrate how to apply the formulas to find the sum of 'n' terms in an arithmetic progression, whether 'n' is finite or infinite, and whether you have the first term, common difference, or the last term of the progression.Key Points of Sum to n Terms of Arithmetic Progression Formula
- Sum of an arithmetic progression with first term 'a' and common difference 'd': Sn = n/2 (2a+(n−1)d) or S n = n/2 (a1+an).
- Sum of an AP of 'n' natural numbers: n(n+1)/2.
Sum to n Terms of Arithmetic Progression Formula FAQs
What is an arithmetic progression (AP)?
An arithmetic progression is a sequence of numbers where the interval between each consecutive term remains consistent.
How can I find the sum of 'n' terms in an AP?
Utilize the formula Sn = n/2 [2a + (n-1)d], where 'a' represents the initial term, 'd' is the fixed difference, and 'n' indicates the quantity of terms.
What is the formula for finding the sum of an infinite AP?
The sum of an infinite AP is ∞ if the common difference (d) is positive and -∞ if d is negative.
How can I find the sum of an AP when I know the first and last terms?
Apply the formula Sn = n/2 [a1 + an], where 'a1' represents the initial term and 'an' signifies the final term in the arithmetic progression (AP).
What's the sum of an AP of 'n' natural numbers?
The sum of an AP of 'n' natural numbers is n(n+1)/2.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App