
The surface area of a sphere Formula encompasses the space covered by the curved external surface of the sphere. When viewed as three-dimensional objects, circular shapes manifest as spheres. Instances of such shapes include a globe or a soccer ball. In this instructional segment, we will delve into comprehending the formula for calculating the surface area of a sphere, as well as mastering the process of surface area determination for a sphere.
What is the Surface Area of a Sphere?
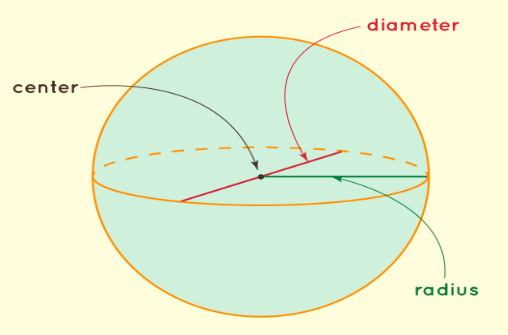
The surface area of a sphere Formula corresponds to the expanse occupied by its external boundary. A sphere represents the three-dimensional embodiment of a circle. The distinction between a sphere and a circle lies in the fact that a circle constitutes a two-dimensional structure (2D shape), whereas a sphere embodies a three-dimensional configuration (3D shape). The quantification of the surface area of a sphere is articulated in terms of square units. Take note of the sphere depicted below, illustrating its center, radius, and diameter.Sphere Definition
A sphere is a three-dimensional, circular-shaped entity characterized by its absence of vertices or edges. Key attributes defining this geometric form encompass the radius, diameter, circumference, and volume.Derivation of Surface Area of Sphere
A sphere boasts a rounded form, leading to the utilization of a comparison with a curved shape, like a cylinder, when determining its surface area. A cylinder presents itself as a shape characterized by a combination of curved and flat surfaces. In a compelling connection, when the radius of a cylinder corresponds with the radius of a sphere, the sphere can be flawlessly accommodated within the cylinder. This alignment equates the height of the cylinder to the height of the sphere, essentially identifying this height as the sphere's diameter. This proposition, ascertained by the celebrated mathematician Archimedes, establishes that when the radii of both the cylinder and sphere are denoted as 'r', the surface area of the sphere aligns with the lateral surface area of the cylinder.Download PDF Surface Area of a Sphere
Therefore, the relationship between the surface area of a sphere and the lateral surface area of a cylinder is encapsulated by the equation: Surface Area of Sphere = Lateral Surface Area of Cylinder The formula for the lateral surface area of a cylinder is 2πrh, where 'r' signifies the radius and 'h' signifies the height of the cylinder. Remarkably, the cylinder's height can equivalently be termed as the diameter of the sphere, given the assumption of a seamless fit between the sphere and the cylinder. Consequently, height of the cylinder = diameter of the sphere = 2r. Within the formula, the surface area of the sphere is rendered as 2πrh; replacing 'h' with the diameter, that is, 2r. Thus, the surface area of the sphere becomes 2πrh = 2πr(2r) = 4πr².Also Check - LCM and HCF Formula
Formula of Surface Area of Sphere
The calculation of a surface area of a sphere Formula relies on its radius. When the sphere's radius is designated as 'r' and its surface area as 'S', the expression for the surface area of the sphere is as follows: Surface Area of Sphere = 4πr²; where 'r' signifies the sphere's radius. Additionally, in terms of the diameter, the surface area of a sphere can be represented as S = 4π(d/2)², where 'd' represents the sphere's diameter.How to Calculate the Surface Area of Sphere?
The surface area of a sphere Formula denotes the expanse occupied by its outer surface. Calculating the surface area of a sphere is achievable through the utilization of its dedicated formula. The procedure for computing the surface area of a sphere is detailed below. To illustrate the process of determining the surface area of a sphere Formula , let's work through an example: Example: Determine the surface area of a spherical ball with a radius measuring 9 inches. Step 1: Take note of the sphere's radius. In this case, the radius of the ball is 9 inches. Step 2: Given the formula for the surface area of a sphere is 4πr², substitute the radius value: surface area of sphere = 4πr² = 4 × 3.14 × 9² = 4 × 3.14 × 81 = 1017.36 Step 3: Consequently, the surface area of the sphere equals 1017.36 square inches.Also Check - Area of a Rectangle Formula
Curved Surface Area of a Sphere Formula
The curved surface area of a sphere encompasses its entire surface since a sphere constitutes a single curved surface. Given the absence of flat surfaces within a sphere's structure, its curved surface area aligns seamlessly with its total surface area. Consequently, the formula for calculating the curved surface area of a sphere is succinctly expressed as: Curved surface area of sphere = 4πr², where 'r' signifies the sphere's radius.Surface Area of a Sphere Formula Examples
Example 1: Calculate the surface area of a sphere with a radius of 20 feet. (Take π = 3.14) Solution: We are provided with the sphere's radius 'r' = 20 feet. The surface area of the sphere can be determined using the formula 4πr², where r = 20: Surface area of the sphere = 4πr² = 4 × π × 20² = 5024 square feet Hence, the surface area of the sphere is 5024 square feet. Example 2: Determine the surface area of a sphere when the radius is provided as 6 units. Solution: We are given the radius 'r' = 6 units. Let's plug in the value of r = 6 units. ⇒ The surface area of the sphere = 4πr² = 4 × π × 6² = 4 × 3.14 × 36 = 452.16 square units Hence, the surface area of the sphere is 452.16 square units. Example 3: Determine whether the following statements are true or false. a.) A sphere is a three-dimensional form of a circle. b.) The curved surface area of a sphere is the total surface area of the sphere because a sphere has just one surface that is curved.Also Check - Area of a Hexagon Formula
Solution: a.) True. A sphere is indeed a three-dimensional representation of a circle. b.) True. The assertion is accurate. The curved surface area of a sphere corresponds to the total surface area since a sphere is characterized by a solitary curved surface. [wp-faq-schema title="Surface area of a Sphere Formula FAQs" accordion=1Surface area of a Sphere Formula FAQs
Define the term Sphere.
A sphere is a three-dimensional, circular-shaped entity characterized by its absence of vertices or edges. Key attributes defining this geometric form encompass the radius, diameter, circumference, and volume.
How many Surfaces does a sphere have?
Indeed, a sphere does not possess any faces. The concept of a face pertains to a flat surface, which is conspicuously absent in a sphere's structure. Consequently, a sphere assumes the form of a three-dimensional shape without faces, accurately described as a faceless three-dimensional (3D) entity.
What is the formula for TSA of a Sphere?
The calculation of a sphere's surface area relies on its radius. When the sphere's radius is designated as 'r' and its surface area as 'S', the expression for the surface area of the sphere is as follows:
Surface Area of Sphere = 4πr²; where 'r' signifies the sphere's radius.
Explain the relation between the CSA of a cylinder and the TSA of a sphere.
The relationship between the surface area of a sphere and the lateral surface area of a cylinder is encapsulated by the equation:
Surface Area of Sphere = Lateral Surface Area of Cylinder
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Check out these Related Articles
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App









