
Surface Areas and Volumes Formula: The surface area formula serves as a mathematical tool to determine the cumulative area covered by all surfaces of a three-dimensional object. To gain a comprehensive understanding, let's delve into the intricate details of surface area formulas applicable to various three-dimensional shapes.
The volume formula provides a mathematical representation that enables the calculation of the overall space enclosed by a three-dimensional object. To gain a deeper insight, let's explore the comprehensive details of volume formulas applied to various three-dimensional shapes.
Also Check - Solid Shapes FormulaWhat Is the Surface Area Formula?
The surface area formula serves the purpose of calculating the combined extent of all surface areas belonging to a three-dimensional object. This formula can be categorized into two distinct types:
- Curved surface area formula, also known as the lateral surface area formula.
- Total surface area formula.
Take a glance at the surface area formulas chart presented below, illustrating the surface area formulas for various three-dimensional shapes.
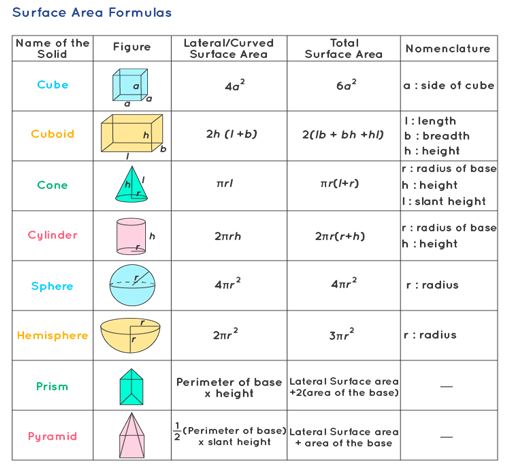
Surface Area Formulas of Different Shapes
In the realm of three-dimensional objects, there exists a distinction between lateral surfaces and base surfaces. The aggregate surface area, known as the total surface area, encompasses both the lateral or curved surface area and the base surface area. In this segment, we will delve into the exploration of surface area formulas pertaining to diverse three-dimensional shapes.
Also Check - Introduction to Graph FormulaSurface Area Formula of Cube
The surface area of a cube accounts for the entirety of the space covered by its six faces. The overarching formula for the cube's surface area is expressed as follows:
The total surface area formula for a cube constitutes the summation of the areas of its vertical surfaces and the base. This can be represented as:
Total Surface Area = 6a², where "a" signifies the side length.
Download PDF Surface Area and Volumes Formula
Alternatively, the lateral surface area formula for a cube entails the summation of the areas of all its lateral side faces. This can be denoted as:
Lateral Surface Area = 4a², where "a" signifies the side length.
Also Check - Line and Angles FormulaSurface Area Formula of Cuboid
The formula for the total surface area of a cuboid is derived by summing up the areas of all six of its faces. This total surface area, as well as the lateral surface area, can be expressed in terms of its dimensions: length (l), breadth (b), and height (h) of the cuboid:
The total surface area of a cuboid, denoted as S, is given by:
S = 2 (lb + bh + lh) units 2
The lateral surface area of a cuboid, denoted as L, is given by:
L = 2h (l + b) units 2
Surface Area Formula of Cone
A cone is a three-dimensional geometric figure characterized by a circular base possessing a radius "r" and a diameter "d". Its distinct feature is its curved surface, leading to the formulation of both its curved surface area formula and total surface area formula. When considering a cone with a base radius of "r" and a slant height of "l", the cone's surface area is defined as:
The total surface area of a cone, represented as "T", is computed using the formula:
T = πr(r + l)
The curved surface area of a cone, denoted as "S", can be determined by the formula:
S = πrl
Also Check - Set FormulaSurface Area Formula of Cylinder
A cylinder possesses a curved surface encompassing two circular bases situated at its opposing ends. When the base radius of the cylinder is "r" and its height is "h", the formula for its surface area is as follows:
The total surface area of a cylinder, denoted as "T", can be calculated using the formula:
T = 2πr (h + r)
The curved surface area of a cylinder, represented as "S", is computed using the formula:
S = 2πrh
Surface Area Formula of Sphere
A sphere is a three-dimensional object characterized by its rounded structure. The surface area of a sphere corresponds to the collective area of its enclosing surfaces. The formula governing the surface area of a sphere is as follows:
⇒ The surface area of a sphere, denoted as "S", is calculated using the formula:
S = 4πr 2 square units.
Surface Area Formula of Hemisphere
A hemisphere constitutes one-half of a sphere. The surface area of a hemisphere corresponds to the complete area covered by its external surface. The surface area formula for a hemisphere is categorized into two distinct types:
The curved surface area of a hemisphere (CSA) is calculated as half of the curved surface area of a full sphere, which is equivalent to half of
½ (4 π r 2 ) = 2 π r 2
, where "r" denotes the hemisphere's radius.
The total surface area of a hemisphere (TSA) encompasses both the curved surface area and the base area, which is given by
curved surface area + Base Area = 2 π r 2 + π r 2 = 3 π r 2
, where "r" represents the hemisphere's radius.
Also Check - Polynomials FormulaSurface Area Formula of Prism
The lateral surface area of a prism comprises the summation of the areas of all its lateral faces, while the total surface area of a prism encompasses both its lateral area and the area of its bases. The surface area formulas applicable to prisms can be described as follows:
The lateral surface area of a prism is equal to the product of the base perimeter and the height of the prism.
The total surface area of a prism is calculated as the sum of the lateral surface area of the prism and twice the area of its bases. This can be expressed as :
(2 × Base Area) + Lateral surface area or (2 × Base Area) + (Base perimeter × height).
There exist seven types of prisms, distinguished by the shapes of their bases. As the bases vary among these types, so do the formulas utilized to determine the surface area of each type of prism.
Also Check - Sequence and Series FormulaWhat is the Volume Formula?
The formula employed to compute the complete capacity that an object can contain in three-dimensional space is referred to as its volume formula. The measurement unit for the volume of a three-dimensional shape is indicated as units³ or cubic units. Please refer to the volume formulas chart below, which illustrates the volume formulas for various three-dimensional shapes.
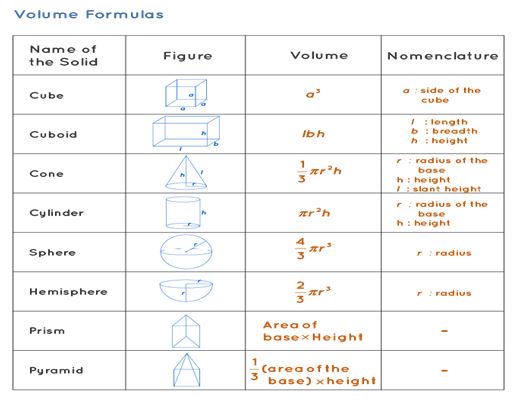
Volume Formulas of 3-D Shapes
It's established that the volume formula serves the purpose of determining the spatial capacity of a three-dimensional object. In the forthcoming section, we'll delve into the comprehension of volume formulas, taking into account the dimensions specific to various three-dimensional shapes.
Volume Formula of Cube
The volume formula of a cube is influenced by the three equal sides of the cube. In a cube, all sides have the same length. The volume of a cube signifies the amount of space enclosed by the cube. The fundamental formula to calculate the volume of a cube is:
The volume of a cube = a × a × a = a 3 cubic units,
cubic units, where 'a' represents the length of the side of the cube.
Alternatively, the volume of a cube can be computed using its diagonal. This formula is given as (√3× d 3 )/9
, where 'd' is the length of the diagonal of the cube.
Volume Formula of Cuboid
To determine the extent of space enclosed by a cuboid, we employ the cuboid's volume formula. The comprehensive formula for calculating the volume of a cuboid is mathematically portrayed as follows:
volume of the cuboid = Base Area × Height cubic units
The base area of cuboid = l × b square units
Therefore, the volume of a cuboid, represented as 'V', is equal to V = l × b × h = lbh units 3
units, where 'l', 'b', and 'h' denote the length, breadth, and height of the cuboid, respectively.
Volume Formula of Cone
For quantifying the space encompassed within a three-dimensional cone, characterized by a circular base with a radius 'r' and height 'h', the volume formula of the cone comes into play. The overarching volume formula for a cone is articulated as follows:
The volume of a cone, denoted as 'V', can be determined using the expression:
In this equation: V = (1/3) πr 2 h cubic units.
'r' stands for the radius of the cone's base (which is circular in shape).
'h' corresponds to the height of the cone.
π is a constant with a value of either 22/7 or approximately 3.142.
Volume Formula of Cylinder
The formula to compute the volume of a cylinder serves the purpose of ascertaining the space enclosed within it. Considering that the base of a right circular cylinder is a circle, and the area of a circle with radius 'r' is πr², the volume of a cylinder is given by:
The volume of a cylinder = πr²h cubic units
In this context:
'r' symbolizes the radius of the cylinder's base (which is circular).
'h' denotes the height of the cylinder.
π is a constant with a value of either 22/7 or approximately 3.142.
Consequently, the volume of a cylinder is directly linked to both its height and the square of its radius. This means that if the radius of the cylinder doubles, its volume becomes four times larger.
Volume Formula of Sphere
A football serves as an apt illustration, resembling the spherical shape. This three-dimensional solid object boasts a rounded structure. The quantity of air contained within a ball is referred to as the volume of a sphere, or in this context, a ball. The volume formula pertinent to a sphere is as follows:
The volume of a sphere = (2/3) πr 2 h
In this scenario:
'r' signifies the radius of the sphere.
'h' represents the height of the sphere.
π is a constant, either valued at 3.142 or 22/7.
Thus, the volume of a sphere is determined as ( 2/3) πr 2 h = (2/3) πr 2 (2r) = (4/3) πr 3 cubic units
Volume Formula of Hemisphere
A hemisphere is precisely half of a sphere, and we can conveniently derive its volume formula by leveraging the sphere's volume formula.
The volume of the hemisphere = (2/3) πr 3 cubic units
In this context:
'r' represents the radius of the hemisphere.
π is a constant, having a value of either 3.142 or 22/7.
Volume Formula of Prism
The formula to calculate the volume of a prism is obtained by multiplying the base area of the prism by its height. Mathematically, it can be stated as:
The volume of a prism, denoted as 'V', is given by V = B × h cube units.
In this equation:
"B" signifies the base area of the prism, measured in square units.
"h" represents the height of the prism, measured in units.
There exist seven distinct types of prisms, each determined by the shape of its base. Consequently, the volume formula of prisms varies according to the specific bases of these prisms. For a deeper understanding of the concept underlying the volume formulas of different prisms, you can explore the concept of the volume of the prism.
Surface Areas and Volumes Formula FAQs
What is the formula used to calculate the volume of a cuboid?
Define the term Surface Area.
Define the term Volume.
What is meant by Base Area?










