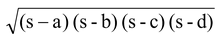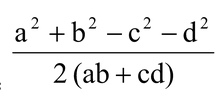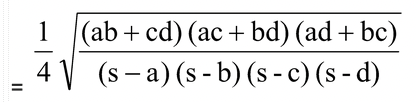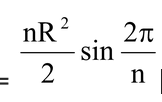Properties of Triangles
Trignometric equations of Class 11
Properties of Triangles
(i) Area of the ΔABC:
The area of ΔABC (denoted by Δ or S) may be expressed in many ways as follows:
(i) Δ = 1/2 bc sin A = 1/2 ca sin B = 1/2 ab sin C.
(ii) Δ =
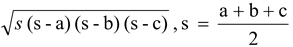
(iii) Δ =
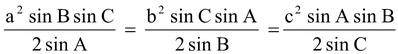
(ii) Sine Rule
In any ΔABC,
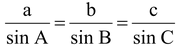
(iii) Cosine Rule
In any ΔABC
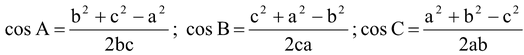
(iv) Projection Rule
In any ΔABC,
a = b cos C + c cos B, b = c cos A + a cos C, c = a cos B + b cos A.
(v) Tangent Rule (Nepier’s Analogy)
In any ΔABC,
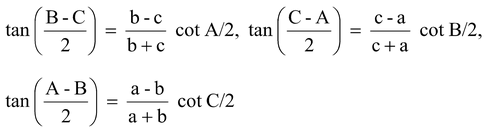
(vi) Trigonometrical Ratios of the Half-Angles of ΔABC
(a)
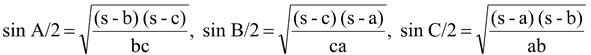
(b)
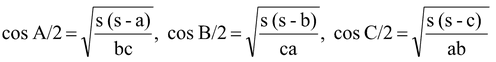
(c)
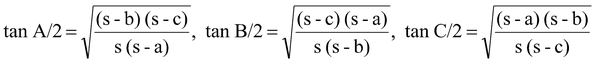
(vii) Formulae for Circum-radius R:
(a)
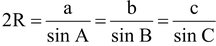
(b)
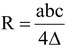
(viii) Formulae for In-radius r:
(a) r = Δ/s
(b) r = (s-a) tan A/2 = (s-b) tan B/2 = (s-c) tan C/2
(c)
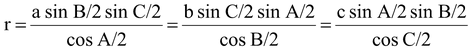
(d) r = 4 R sin A/2 sin B/2 sin C/2
(ix) Formulae for ex-radii r 1 , r 2 , r 3 :
(a)
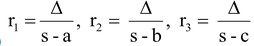
(b) r 1 = s tan A/2, r 2 = s tan B/2, r 3 = s tan C/2
(c)
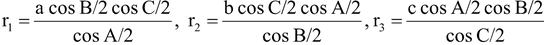
(d) r 1 = 4R sin A/2 cos B/2 cos C/2, r 2 = 4R cos A/2 sin B/2 cos C/2,
r 3 = 4R cos A/2 cos B/2 sin C/2.
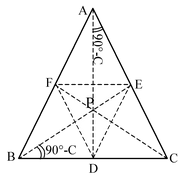
(x) Orthocentre and Pedal triangle of any Triangle:
|
Let ABC be any triangle and let the perpendiculars AD, BE and CF from vertices A,B and C on opposite BC, CA and AB respectively, meet at P. then P is the orthocentre of the ΔABC. (Fig. Tri.1) the triangle DEF, which is formed by joining the feet of these perpendiculars, is called the pedal triangle of ΔABC. |
Fig. Tri.1 |
(xi) The distances of the orthocentre from the vertices and the sides:
(a) PA = 2R cos A, PB = 2R cos B, PC = 2R cos C
(b) PD = 2R cos B cos C, PE = 2R cos C cos A, PF = 2R cos A cos B.
(xii) Sides and Angles of the Pedal Triangle:
(i) EF = a cos A, DF = b cos B, DE = c cos C
(ii) ∠ EDF = 180° - 2A, ∠DEF = 180° - 2B, ∠EFD = 180° - 2C
(xiii) Length of the Medians:
If AD, BE & CF are the medians of the triangle ABC then
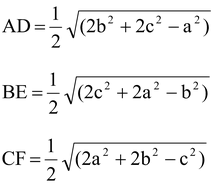
(xiv) Distance between the circumcentre and the Orthocentre:
If ‘O’ is the circumcentre and ‘P’ is the orthocentre then
OP = R
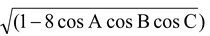
(xv) Distance between the Circumcentre and the Incentre:
If ‘O’ is the circumcentre and ‘I’ is the Incentre then
OI = R
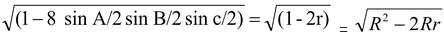
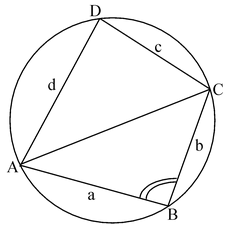
(xvi) Ptolemy’s Theorem:
In a cyclic quadrilateral ABCD.
AC. BD = AB . CD + BC . AD.
(xvii) Cyclic Quadrilateral:
|
(a) Area of the cyclic quadrilateral
=
when 2s = a + b + c + d
(b) Cos B =
(c) Radius of the circum circle
=
|
Fig. Tri.2 |
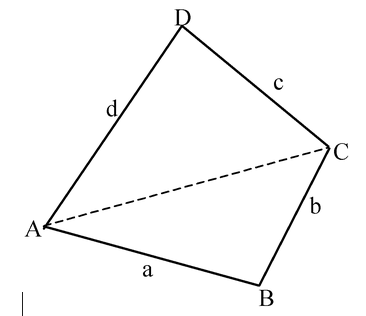
(xviii) Area of the Quadrilateral:
|
Let ∠B + ∠D = 2α then Area Δ of the quadrilateral is given by Δ2 = (s-a) (s-b) (s-c) (s-d) – abcd cos α Corollary I: If d = 0, then the quadrilateral becomes a triangle. Corollary II: The quadrilateral, whose sides are given, has the greatest area when it can be inscribed in a circle. |
Fig. Tri.3 |
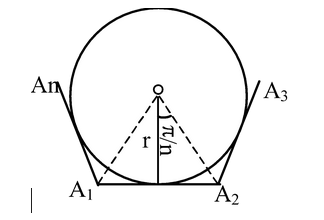
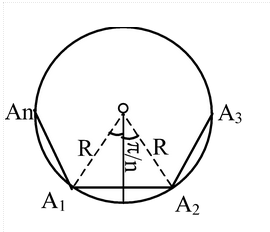
(xix) Regular Polygon:
|
Let A1, A2, . . . An be a regular polygon of n sides each of length a. (a) Inscribed circle of a regular polygon of n sides:Area = nr2 tan π/n Radius r = a/2 cot π/n |
Fig. Tri.4 |
(b) Circumscribed circle of a regular polygon of n sides:
Area =
Radius = R = a/2 cosec π/n |
Fig. Tri.5 |
(xx) Some More Relations Regarding a Triangle:
(a) a cos A + b cos B + c cos C = 4R sin A sin B sin C.
(b) a cot A + b cot B + c cot C = 2 (R+r)
(c) r 1 + r 2 + r 3 = 4R + r.
(d) r 1 r 2 + r 2 r 3 + r 3 r 1 = s 2 .
Related Topics