
NCERT Solutions For Class 12 Physics Chapter 13 Nuclei
NCERT Solutions For Class 12 Physics Chapter 13 Nuclei is prepared by our senior and renowned teachers of Physics Wallah primary focus while solving these questions of class-12 in NCERT textbook, also do read theory of this Chapter 13 Nuclei while going before solving the NCERT questions. You can download and share NCERT Solutions of Class 12 Physics from Physics Wallah.
NCERT Solutions For Class 12 Physics Chapter 13 Overview
NCERT Solutions for Class 12 Physics Chapter 13 covers these important topics. Students are encouraged to carefully study each topic in order to completely understand the concepts taught in the chapter and make optimal use of the provided solutions.
These solutions were designed by Physics Wallah professors to improve understanding of the concepts covered in the chapter. The goal is for students to easily obtain good exam scores.NCERT Solutions For Class 12 Physics Chapter 13 PDF
To help students understand and practise chapter topics, our team of experts at Physics Wallah has developed thorough solutions for NCERT Class 12 Physics, Chapter 13. The purpose of these questions is to make explanations easier to understand for students. You can use the following link to download the NCERT Solutions for Class 12 Physics, Chapter 13 PDF:NCERT Solutions Class 12 Physics Chapter 13 PDF Download Link
NCERT Solutions For Class 12 Physics Chapter 13
Answer The Following Question Answer NCERT Solutions For Class 12 Physics Chapter 13 Nuclei:
Question 1. (a) Two stable isotopes of lithium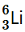 and
and
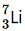 have respective abundances of 7.5% and 92.5%. These isotopes have masses 6.01512 u and 7.01600 u, respectively. Find the atomic mass of lithium.
(b) Boron has two stable isotopes,
have respective abundances of 7.5% and 92.5%. These isotopes have masses 6.01512 u and 7.01600 u, respectively. Find the atomic mass of lithium.
(b) Boron has two stable isotopes,
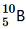 and
and
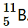 . Their respective masses are 10.01294 u and 11.00931 u, and the atomic mass of boron is 10.811 u. Find the abundances of
. Their respective masses are 10.01294 u and 11.00931 u, and the atomic mass of boron is 10.811 u. Find the abundances of
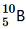 and
and
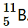 .
Solution :
(a) Mass of lithium isotope
.
Solution :
(a) Mass of lithium isotope
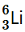 , m1 = 6.01512 u
Mass of lithium isotope
, m1 = 6.01512 u
Mass of lithium isotope
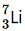 , m2 = 7.01600 u
Abundance of
, m2 = 7.01600 u
Abundance of
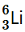 , η1= 7.5%
Abundance of
, η1= 7.5%
Abundance of
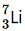 , η2= 92.5%
The atomic mass of lithium atom is given as:
, η2= 92.5%
The atomic mass of lithium atom is given as:
 =
=
 = 6.940934 u.
(b) Mass of boron isotope
= 6.940934 u.
(b) Mass of boron isotope
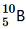 , m1 = 10.01294 u
Mass of boron isotope
, m1 = 10.01294 u
Mass of boron isotope
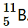 , m2 = 11.00931 u
Abundance of
, m2 = 11.00931 u
Abundance of
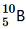 , η1 = x%
Abundance of
, η1 = x%
Abundance of
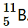 , η2= (100 − x)%
Atomic mass of boron, m = 10.811 u
The atomic mass of boron atom is given as:
, η2= (100 − x)%
Atomic mass of boron, m = 10.811 u
The atomic mass of boron atom is given as:

 x = 19.821/0.99637 = 19.89%
And 100 − x = 80.11%
Hence, the abundance of
x = 19.821/0.99637 = 19.89%
And 100 − x = 80.11%
Hence, the abundance of
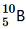 is 19.89% and that of
is 19.89% and that of
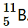 is 80.11%.
Question
2. The three stable isotopes of neon:
is 80.11%.
Question
2. The three stable isotopes of neon:
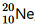 ,
,
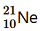 and
and
 have respective abundances of 90.51%, 0.27% and 9.22%. The atomic masses of the three isotopes are 19.99 u, 20.99 u and 21.99 u, respectively. Obtain the average atomic mass of neon.
Solution :
Atomic mass of
have respective abundances of 90.51%, 0.27% and 9.22%. The atomic masses of the three isotopes are 19.99 u, 20.99 u and 21.99 u, respectively. Obtain the average atomic mass of neon.
Solution :
Atomic mass of
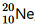 , m1= 19.99 u
Abundance of
, m1= 19.99 u
Abundance of
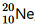 , η1 = 90.51%
Atomic mass of
, η1 = 90.51%
Atomic mass of
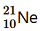 , m2 = 20.99 u
Abundance of
, m2 = 20.99 u
Abundance of
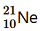 , η2 = 0.27%
Atomic mass of
, η2 = 0.27%
Atomic mass of
 , m3 = 21.99 u
Abundance of
, m3 = 21.99 u
Abundance of
 , η3 = 9.22%
The average atomic mass of neon is given as:
, η3 = 9.22%
The average atomic mass of neon is given as:
 = 20.1771u
Question
3. Obtain the binding energy (in MeV) of a nitrogen nucleus
= 20.1771u
Question
3. Obtain the binding energy (in MeV) of a nitrogen nucleus
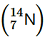 , given
, given
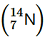 =14.00307 u
Solution :
Atomic mass of nitrogen
=14.00307 u
Solution :
Atomic mass of nitrogen
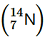 , m = 14.00307 u
A nucleus of nitrogen
, m = 14.00307 u
A nucleus of nitrogen
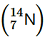 contains 7 protons and 7 neutrons.
Hence, the mass defect of this nucleus, Δm = 7mH + 7mn − m
Where,
Mass of a proton, mH = 1.007825 u
Mass of a neutron, mn= 1.008665 u
∴Δm = 7 × 1.007825 + 7 × 1.008665 − 14.00307
= 7.054775 + 7.06055 − 14.00307
= 0.11236 u
But 1 u = 931.5 MeV/c2
∴Δm = 0.11236 × 931.5 MeV/c2
Hence, the binding energy of the nucleus is given as:
Eb = Δmc2
Where,
c = Speed of light
∴Eb = 0.11236 × 931.5 (MeV/c2)
= 104.66334 MeV
Hence, the binding energy of a nitrogen nucleus is 104.66334 MeV.
Question
4. Obtain the binding energy of the nuclei
contains 7 protons and 7 neutrons.
Hence, the mass defect of this nucleus, Δm = 7mH + 7mn − m
Where,
Mass of a proton, mH = 1.007825 u
Mass of a neutron, mn= 1.008665 u
∴Δm = 7 × 1.007825 + 7 × 1.008665 − 14.00307
= 7.054775 + 7.06055 − 14.00307
= 0.11236 u
But 1 u = 931.5 MeV/c2
∴Δm = 0.11236 × 931.5 MeV/c2
Hence, the binding energy of the nucleus is given as:
Eb = Δmc2
Where,
c = Speed of light
∴Eb = 0.11236 × 931.5 (MeV/c2)
= 104.66334 MeV
Hence, the binding energy of a nitrogen nucleus is 104.66334 MeV.
Question
4. Obtain the binding energy of the nuclei
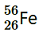 and
and
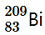 in units of MeV from the following data:
m
in units of MeV from the following data:
m
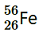 = 55.934939 u m
= 55.934939 u m
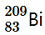 = 208.980388 u
Solution :
Atomic mass of
= 208.980388 u
Solution :
Atomic mass of
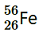 , m1 = 55.934939 u
, m1 = 55.934939 u
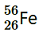 nucleus has 26 protons and (56 − 26) = 30 neutrons
Hence, the mass defect of the nucleus, Δm = 26 × mH + 30 × mn − m1
Where,
Mass of a proton, mH = 1.007825 u
Mass of a neutron, mn = 1.008665 u
∴Δm = 26 × 1.007825 + 30 × 1.008665 − 55.934939
= 26.20345 + 30.25995 − 55.934939
= 0.528461 u
But 1 u = 931.5 MeV/c2
∴Δm = 0.528461 × 931.5 MeV/c2
The binding energy of this nucleus is given as:
Eb1 = Δmc2
Where,
c = Speed of light
∴Eb1 = 0.528461 × 931.5 (MeV/c2)
= 492.26 MeV
Average binding energy per nucleon 492.26/56 = 8.79 MeV
Atomic mass of
nucleus has 26 protons and (56 − 26) = 30 neutrons
Hence, the mass defect of the nucleus, Δm = 26 × mH + 30 × mn − m1
Where,
Mass of a proton, mH = 1.007825 u
Mass of a neutron, mn = 1.008665 u
∴Δm = 26 × 1.007825 + 30 × 1.008665 − 55.934939
= 26.20345 + 30.25995 − 55.934939
= 0.528461 u
But 1 u = 931.5 MeV/c2
∴Δm = 0.528461 × 931.5 MeV/c2
The binding energy of this nucleus is given as:
Eb1 = Δmc2
Where,
c = Speed of light
∴Eb1 = 0.528461 × 931.5 (MeV/c2)
= 492.26 MeV
Average binding energy per nucleon 492.26/56 = 8.79 MeV
Atomic mass of
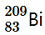 , m2 = 208.980388 u
, m2 = 208.980388 u
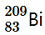 nucleus has 83 protons and (209 − 83) 126 neutrons.
Hence, the mass defect of this nucleus is given as:
Δm' = 83 × mH + 126 × mn − m2
Where,
Mass of a proton, mH = 1.007825 u
Mass of a neutron, mn = 1.008665 u
∴Δm' = 83 × 1.007825 + 126 × 1.008665 − 208.980388
= 83.649475 + 127.091790 − 208.980388
= 1.760877 u
But 1 u = 931.5 MeV/c2
∴Δm' = 1.760877 × 931.5 MeV/c2
Hence, the binding energy of this nucleus is given as:
Eb2 = Δm'c2
= 1.760877 × 931.5(MeV/c2)
= 1640.26 MeV
Average bindingenergy per nucleon = 1640.26/209 = 7.848 MeV
Question
5. A given coin has a mass of 3.0 g. Calculate the nuclear energy that would be required to separate all the neutrons and protons from each other. For simplicity assume that the coin is entirely made of
nucleus has 83 protons and (209 − 83) 126 neutrons.
Hence, the mass defect of this nucleus is given as:
Δm' = 83 × mH + 126 × mn − m2
Where,
Mass of a proton, mH = 1.007825 u
Mass of a neutron, mn = 1.008665 u
∴Δm' = 83 × 1.007825 + 126 × 1.008665 − 208.980388
= 83.649475 + 127.091790 − 208.980388
= 1.760877 u
But 1 u = 931.5 MeV/c2
∴Δm' = 1.760877 × 931.5 MeV/c2
Hence, the binding energy of this nucleus is given as:
Eb2 = Δm'c2
= 1.760877 × 931.5(MeV/c2)
= 1640.26 MeV
Average bindingenergy per nucleon = 1640.26/209 = 7.848 MeV
Question
5. A given coin has a mass of 3.0 g. Calculate the nuclear energy that would be required to separate all the neutrons and protons from each other. For simplicity assume that the coin is entirely made of
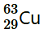 atoms (of mass 62.92960 u).
Solution :
Mass of a copper coin, m’ = 3 g
Atomic mass of
atoms (of mass 62.92960 u).
Solution :
Mass of a copper coin, m’ = 3 g
Atomic mass of
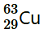 atom, m = 62.92960 u
The total number of
atom, m = 62.92960 u
The total number of
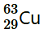 atoms in the coin
atoms in the coin
 Where,
NA = Avogadro’s number = 6.023 × 1023 atoms /g
Mass number = 63 g
Where,
NA = Avogadro’s number = 6.023 × 1023 atoms /g
Mass number = 63 g

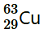 nucleus has 29 protons and (63 − 29) 34 neutrons
∴Mass defect of this nucleus, Δm' = 29 × mH + 34 × mn − m
Where,
Mass of a proton, mH = 1.007825 u
Mass of a neutron, mn = 1.008665 u
∴Δm' = 29 × 1.007825 + 34 × 1.008665 − 62.9296
= 0.591935 u
Mass defect of all the atoms present in the coin, Δm = 0.591935 × 2.868 × 1022
= 1.69766958 × 1022 u
But 1 u = 931.5 MeV/c2
∴Δm = 1.69766958 × 1022 × 931.5 MeV/c2
Hence, the binding energy of the nuclei of the coin is given as:
Eb= Δmc2
= 1.69766958 × 1022 × 931.5 (MeV/c2)
= 1.581 × 1025 MeV
But 1 MeV = 1.6 × 10−13 J
Eb = 1.581 × 1025 × 1.6 × 10−13
= 2.5296 × 1012 J
This much energy is required to separate all the neutrons and protons from the given coin.
Question
6. Write nuclear reaction equations for
(i) α-decay of
nucleus has 29 protons and (63 − 29) 34 neutrons
∴Mass defect of this nucleus, Δm' = 29 × mH + 34 × mn − m
Where,
Mass of a proton, mH = 1.007825 u
Mass of a neutron, mn = 1.008665 u
∴Δm' = 29 × 1.007825 + 34 × 1.008665 − 62.9296
= 0.591935 u
Mass defect of all the atoms present in the coin, Δm = 0.591935 × 2.868 × 1022
= 1.69766958 × 1022 u
But 1 u = 931.5 MeV/c2
∴Δm = 1.69766958 × 1022 × 931.5 MeV/c2
Hence, the binding energy of the nuclei of the coin is given as:
Eb= Δmc2
= 1.69766958 × 1022 × 931.5 (MeV/c2)
= 1.581 × 1025 MeV
But 1 MeV = 1.6 × 10−13 J
Eb = 1.581 × 1025 × 1.6 × 10−13
= 2.5296 × 1012 J
This much energy is required to separate all the neutrons and protons from the given coin.
Question
6. Write nuclear reaction equations for
(i) α-decay of
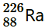 (ii) α-decay of
(ii) α-decay of
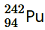 (iii) β−-decay of
(iii) β−-decay of
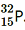 (iv) β−-decay of
(iv) β−-decay of
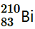 (v) β+-decay of
(v) β+-decay of
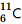 (vi) β+-decay of
(vi) β+-decay of
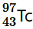 (vii) Electron capture of
(vii) Electron capture of
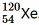 Solution :
α is a nucleus of helium
Solution :
α is a nucleus of helium
 and β is an electron (e− for β− and e+ for β+). In every α-decay, there is a loss of 2 protons and 4 neutrons. In every β+-decay, there is a loss of 1 proton and a neutrino is emitted from the nucleus. In every β−-decay, there is a gain of 1 proton and an antineutrino is emitted from the nucleus.
For the given cases, the various nuclear reactions can be written as:
and β is an electron (e− for β− and e+ for β+). In every α-decay, there is a loss of 2 protons and 4 neutrons. In every β+-decay, there is a loss of 1 proton and a neutrino is emitted from the nucleus. In every β−-decay, there is a gain of 1 proton and an antineutrino is emitted from the nucleus.
For the given cases, the various nuclear reactions can be written as:
 Question
7. A radioactive isotope has a half-life of T years. How long will it take the activity to reduce to a) 3.125%, b) 1% of its original value?
Solution :
Half-life of the radioactive isotope = T years
Original amount of the radioactive isotope = N0
(a) After decay, the amount of the radioactive isotope = N
It is given that only 3.125% of N0 remains after decay. Hence, we can write:
Question
7. A radioactive isotope has a half-life of T years. How long will it take the activity to reduce to a) 3.125%, b) 1% of its original value?
Solution :
Half-life of the radioactive isotope = T years
Original amount of the radioactive isotope = N0
(a) After decay, the amount of the radioactive isotope = N
It is given that only 3.125% of N0 remains after decay. Hence, we can write:
 Where,
λ = Decay constant
t = Time
Where,
λ = Decay constant
t = Time
 Hence, the isotope will take about 5T years to reduce to 3.125% of its original value.
(b) After decay, the amount of the radioactive isotope = N
It is given that only 1% of N0 remains after decay. Hence, we can write:
Hence, the isotope will take about 5T years to reduce to 3.125% of its original value.
(b) After decay, the amount of the radioactive isotope = N
It is given that only 1% of N0 remains after decay. Hence, we can write:
 Hence, the isotope will take about 6.645T years to reduce to 1% of its original value.
Question
8. The normal activity of living carbon-containing matter is found to be about 15 decays per minute for every gram of carbon. This activity arises from the small proportion of radioactive
Hence, the isotope will take about 6.645T years to reduce to 1% of its original value.
Question
8. The normal activity of living carbon-containing matter is found to be about 15 decays per minute for every gram of carbon. This activity arises from the small proportion of radioactive
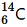 present with the stable carbon isotope
present with the stable carbon isotope
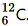 . When the organism is dead, its interaction with the atmosphere (which maintains the above equilibrium activity) ceases and its activity begins to drop. From the known half-life (5730 years) of
. When the organism is dead, its interaction with the atmosphere (which maintains the above equilibrium activity) ceases and its activity begins to drop. From the known half-life (5730 years) of
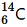 , and the measured activity, the age of the specimen can be approximately estimated. This is the principle of
, and the measured activity, the age of the specimen can be approximately estimated. This is the principle of
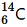 dating used in archaeology. Suppose a specimen from Mohenjodaro gives an activity of 9 decays per minute per gram of carbon. Estimate the approximate age of the Indus-Valley civilisation.
Solution :
Decay rate of living carbon-containing matter, R = 15 decay/min
Let N be the number of radioactive atoms present in a normal carbon- containing matter.
Half life of
dating used in archaeology. Suppose a specimen from Mohenjodaro gives an activity of 9 decays per minute per gram of carbon. Estimate the approximate age of the Indus-Valley civilisation.
Solution :
Decay rate of living carbon-containing matter, R = 15 decay/min
Let N be the number of radioactive atoms present in a normal carbon- containing matter.
Half life of
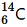 ,
,
 = 5730 years
The decay rate of the specimen obtained from the Mohenjodaro site:
R' = 9 decays/min
Let N' be the number of radioactive atoms present in the specimen during the Mohenjodaro period.
Therefore, we can relate the decay constant, λand time, t as:
= 5730 years
The decay rate of the specimen obtained from the Mohenjodaro site:
R' = 9 decays/min
Let N' be the number of radioactive atoms present in the specimen during the Mohenjodaro period.
Therefore, we can relate the decay constant, λand time, t as:
 Hence, the approximate age of the Indus-Valley civilisation is 4223.5 years.
Question
9. Obtain the amount of
Hence, the approximate age of the Indus-Valley civilisation is 4223.5 years.
Question
9. Obtain the amount of
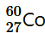 necessary to provide a radioactive source of 8.0 mCi strength. The half-life of
necessary to provide a radioactive source of 8.0 mCi strength. The half-life of
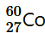 is 5.3 years.
Solution :
The strength of the radioactive source is given as:
dN/dt = 8.0mCi
Where,
N = Required number of atoms
Half-life of
is 5.3 years.
Solution :
The strength of the radioactive source is given as:
dN/dt = 8.0mCi
Where,
N = Required number of atoms
Half-life of
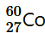 ,
,
 = 5.3 years
= 5.3 × 365 × 24 × 60 × 60
= 1.67 × 108 s
For decay constant λ, we have the rate of decay as:
= 5.3 years
= 5.3 × 365 × 24 × 60 × 60
= 1.67 × 108 s
For decay constant λ, we have the rate of decay as:
 For
For
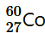 :
Mass of 6.023 × 1023 (Avogadro’s number) atoms = 60 g
∴Mass of 7.133 x 10
16
atoms
= 60 x 7.133 x 10
16
/6.023 x 10
23
= 7.106 x 10
-6
g
Hence, the amount of
:
Mass of 6.023 × 1023 (Avogadro’s number) atoms = 60 g
∴Mass of 7.133 x 10
16
atoms
= 60 x 7.133 x 10
16
/6.023 x 10
23
= 7.106 x 10
-6
g
Hence, the amount of
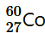 necessary for the purpose is 7.106 × 10−6 g.
Question
10. The half-life of
necessary for the purpose is 7.106 × 10−6 g.
Question
10. The half-life of
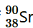 is 28 years. What is the disintegration rate of 15 mg of this isotope?
Solution :
Half life of
is 28 years. What is the disintegration rate of 15 mg of this isotope?
Solution :
Half life of
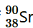 ,
,
 = 28 years
= 28 × 365 × 24 × 60 × 60
= 8.83 × 108 s
Mass of the isotope, m = 15 mg
90 g of
= 28 years
= 28 × 365 × 24 × 60 × 60
= 8.83 × 108 s
Mass of the isotope, m = 15 mg
90 g of
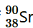 atom contains 6.023 × 1023 (Avogadro’s number) atoms.
Therefore, 15 mg of
atom contains 6.023 × 1023 (Avogadro’s number) atoms.
Therefore, 15 mg of
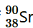 contains:
contains:
 Rate of disintegration,
Rate of disintegration,
 Where,
Where,
 Hence, the disintegration rate of 15 mg of the given isotope is
7.878 × 1010 atoms/s.]
Question
11. Obtain approximately the ratio of the nuclear radii of the gold isotope
Hence, the disintegration rate of 15 mg of the given isotope is
7.878 × 1010 atoms/s.]
Question
11. Obtain approximately the ratio of the nuclear radii of the gold isotope
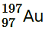 and the silver isotope
and the silver isotope
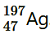 .
Solution :
Nuclear radius of the gold isotope
.
Solution :
Nuclear radius of the gold isotope
 Nuclear radius of the silver isotope
Nuclear radius of the silver isotope
 Mass number of gold, AAu = 197
Mass number of silver, AAg = 107
The ratio of the radii of the two nuclei is related with their mass numbers as:
Mass number of gold, AAu = 197
Mass number of silver, AAg = 107
The ratio of the radii of the two nuclei is related with their mass numbers as:
 Hence, the ratio of the nuclear radii of the gold and silver isotopes is about 1.23.
Question
12. Find the Q-value and the kinetic energy of the emitted α-particle in the α-decay of (a)
Hence, the ratio of the nuclear radii of the gold and silver isotopes is about 1.23.
Question
12. Find the Q-value and the kinetic energy of the emitted α-particle in the α-decay of (a)
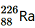 and (b)
and (b)
 .
Given m
.
Given m
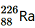 = 226.02540 u,m
= 226.02540 u,m
 = 222.01750 u,
= 222.01750 u,
 = 220.01137 u,
= 220.01137 u,
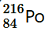 = 216.00189 u.
Solution :
(a) Alpha particle decay of
= 216.00189 u.
Solution :
(a) Alpha particle decay of
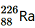 emits a helium nucleus. As a result, its mass number reduces to (226 − 4) 222 and its atomic number reduces to (88 − 2) 86. This is shown in the following nuclear reaction.
emits a helium nucleus. As a result, its mass number reduces to (226 − 4) 222 and its atomic number reduces to (88 − 2) 86. This is shown in the following nuclear reaction.
 Q-value of
emitted α-particle = (Sum of initial mass − Sum of final mass) c2
Where,
c = Speed of light
It is given that:
Q-value of
emitted α-particle = (Sum of initial mass − Sum of final mass) c2
Where,
c = Speed of light
It is given that:
 Q-value = [226.02540 − (222.01750 + 4.002603)] u c2
= 0.005297 u c2
But 1 u = 931.5 MeV/c2
∴Q = 0.005297 × 931.5 ≈ 4.94 MeV
Kinetic energy of the α-particle =
Q-value = [226.02540 − (222.01750 + 4.002603)] u c2
= 0.005297 u c2
But 1 u = 931.5 MeV/c2
∴Q = 0.005297 × 931.5 ≈ 4.94 MeV
Kinetic energy of the α-particle =
 = (222/226) x 4.94 = 4.85 MeV
(b) Alpha particle decay of
= (222/226) x 4.94 = 4.85 MeV
(b) Alpha particle decay of
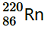 is shown by the following nuclear reaction.
is shown by the following nuclear reaction.
 It is given that:
Mass of
It is given that:
Mass of
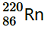 = 220.01137 u
Mass of
= 220.01137 u
Mass of
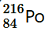 = 216.00189 u
∴ Q-value = [220.01137 - (216.00189 +.00260)] × 931.5
≈ 641 MeV
Kinetic energy of the α-particle = (220-4/220) x 6.41
= 6.29 MeV
Question
13. The radionuclide 11C decays according to
= 216.00189 u
∴ Q-value = [220.01137 - (216.00189 +.00260)] × 931.5
≈ 641 MeV
Kinetic energy of the α-particle = (220-4/220) x 6.41
= 6.29 MeV
Question
13. The radionuclide 11C decays according to
 The maximum energy of the emitted positron is 0.960 MeV.
Given the mass values:
The maximum energy of the emitted positron is 0.960 MeV.
Given the mass values:
 calculate Q and compare it with the maximum energy of the positron emitted
Solution :
The given nuclear reaction is:
calculate Q and compare it with the maximum energy of the positron emitted
Solution :
The given nuclear reaction is:
 Atomic mass of m (
Atomic mass of m (
 ) = 11.011434 u
Atomic mass of
) = 11.011434 u
Atomic mass of
 = 11.009305 u
Maximum energy possessed by the emitted positron = 0.960 MeV
The change in the Q-value (ΔQ) of the nuclear masses of the
= 11.009305 u
Maximum energy possessed by the emitted positron = 0.960 MeV
The change in the Q-value (ΔQ) of the nuclear masses of the
 nucleus is given as:
nucleus is given as:
 ....(i)
Where,
me = Mass of an electron or positron = 0.000548 u
c = Speed of light
m’ = Respective nuclear masses
If atomic masses are used instead of nuclear masses, then we have to add 6 me in the case of
11
Cand 5 me in the case of
11
B.
Hence, equation (1) reduces to:
....(i)
Where,
me = Mass of an electron or positron = 0.000548 u
c = Speed of light
m’ = Respective nuclear masses
If atomic masses are used instead of nuclear masses, then we have to add 6 me in the case of
11
Cand 5 me in the case of
11
B.
Hence, equation (1) reduces to:
 ∴ΔQ = [11.011434 − 11.009305 − 2 × 0.000548] c2
= (0.001033 c2) u
But 1 u = 931.5 Mev/c2
∴ΔQ = 0.001033 × 931.5 ≈ 0.962 MeV
The value of Q is almost comparable to the maximum energy of the emitted positron.
Question
14. The nucleus
∴ΔQ = [11.011434 − 11.009305 − 2 × 0.000548] c2
= (0.001033 c2) u
But 1 u = 931.5 Mev/c2
∴ΔQ = 0.001033 × 931.5 ≈ 0.962 MeV
The value of Q is almost comparable to the maximum energy of the emitted positron.
Question
14. The nucleus
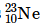 decays by
decays by
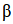 emission. Write down the
emission. Write down the
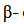 decay equation and determine the maximum kinetic energy of the electrons emitted. Given that:
decay equation and determine the maximum kinetic energy of the electrons emitted. Given that:
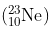 = 22.994466 u
= 22.994466 u
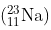 = 22.989770 u.
Solution :
= 22.989770 u.
Solution :
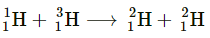 (ii)
(ii)
 Atomic masses are given to be
Atomic masses are given to be
 Solution :
(i) The given nuclear reaction is:
Solution :
(i) The given nuclear reaction is:
 It is given that:
It is given that:
 According to the question, the Q-value of the reaction can be written as:
According to the question, the Q-value of the reaction can be written as:
 The negativeQ-value of the reaction shows that the reaction is endothermic.
(ii) The given nuclear reaction is:
The negativeQ-value of the reaction shows that the reaction is endothermic.
(ii) The given nuclear reaction is:
 It is given that:
It is given that:
 The Q-value of this reaction is given as
The Q-value of this reaction is given as
 The positive Q-value of the reaction shows that the reaction is exothermic.
Question 16:
The positive Q-value of the reaction shows that the reaction is exothermic.
Question 16:
 Solution :
The fission of
Solution :
The fission of
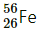 can be given as:
can be given as:
 It is given that:
It is given that:
 The Q-value of this nuclear reaction is given as:
The Q-value of this nuclear reaction is given as:
 The Q-value of the fission is negative. Therefore, the fission is not possible energetically. For an energetically-possible fission reaction, the Q-value must be positive.
The Q-value of the fission is negative. Therefore, the fission is not possible energetically. For an energetically-possible fission reaction, the Q-value must be positive.
 Solution :
Average energy released per fission of
Solution :
Average energy released per fission of
 ,
,
 Amount of pure
Amount of pure
 , m = 1 kg = 1000 g
NA= Avogadro number = 6.023 × 1023
Mass number of
, m = 1 kg = 1000 g
NA= Avogadro number = 6.023 × 1023
Mass number of
 = 239 g
= 239 g

 Solution :
Solution :

 Question
19. How long can an electric lamp of 100W be kept glowing by fusion of 2.0 kg of deuterium? Take the fusion reaction as
Question
19. How long can an electric lamp of 100W be kept glowing by fusion of 2.0 kg of deuterium? Take the fusion reaction as
 Solution :
The given fusion reaction is:
Solution :
The given fusion reaction is:
 Amount of deuterium, m = 2 kg
1 mole, i.e., 2 g of deuterium contains 6.023 × 1023 atoms.
Amount of deuterium, m = 2 kg
1 mole, i.e., 2 g of deuterium contains 6.023 × 1023 atoms.
 It can be inferred from the given reaction that when two atoms of deuterium fuse, 3.27 MeV energy is released.
∴Total energy per nucleus released in the fusion reaction:
It can be inferred from the given reaction that when two atoms of deuterium fuse, 3.27 MeV energy is released.
∴Total energy per nucleus released in the fusion reaction:
 Question
20. Calculate the height of the potential barrier for a head on collision of two deuterons. (Hint: The height of the potential barrier is given by the Coulomb repulsion between the two deuterons when they just touch each other. Assume that they can be taken as hard spheres of radius 2.0 fm.)
Solution :
When two deuterons collide head-on, the distance between their centres, d is given as:
Radius of 1st deuteron + Radius of 2nd deuteron
Radius of a deuteron nucleus = 2 fm = 2 × 10−15 m
∴d = 2 × 10−15 + 2 × 10−15 = 4 × 10−15 m
Charge on a deuteron nucleus = Charge on an electron = e = 1.6 × 10−19 C
Potential energy of the two-deuteron system:
Question
20. Calculate the height of the potential barrier for a head on collision of two deuterons. (Hint: The height of the potential barrier is given by the Coulomb repulsion between the two deuterons when they just touch each other. Assume that they can be taken as hard spheres of radius 2.0 fm.)
Solution :
When two deuterons collide head-on, the distance between their centres, d is given as:
Radius of 1st deuteron + Radius of 2nd deuteron
Radius of a deuteron nucleus = 2 fm = 2 × 10−15 m
∴d = 2 × 10−15 + 2 × 10−15 = 4 × 10−15 m
Charge on a deuteron nucleus = Charge on an electron = e = 1.6 × 10−19 C
Potential energy of the two-deuteron system:
 Question
21. From the relation R = R0A1/3, where R0 is a constant and A is the mass number of a nucleus, show that the nuclear matter density is nearly constant (i.e. independent of A).
Solution :
We have the expression for nuclear radius as:
R = R0A1/3
Where,
R0 = Constant.
A = Mass number of the nucleus
Question
21. From the relation R = R0A1/3, where R0 is a constant and A is the mass number of a nucleus, show that the nuclear matter density is nearly constant (i.e. independent of A).
Solution :
We have the expression for nuclear radius as:
R = R0A1/3
Where,
R0 = Constant.
A = Mass number of the nucleus

 Solution :
Solution :

 Question
23
Question
23
 Solution :
Average atomic mass of magnesium, m = 24.312 u
Solution :
Average atomic mass of magnesium, m = 24.312 u

 Solution :
Solution :

 Question
25. A source contains two phosphorous radio nuclides
Question
25. A source contains two phosphorous radio nuclides
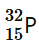 (T1/2 = 14.3d) and
(T1/2 = 14.3d) and
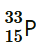 (T1/2 = 25.3d). Initially, 10% of the decays come from
(T1/2 = 25.3d). Initially, 10% of the decays come from
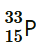 . How long one must wait until 90% do so?
Solution :
. How long one must wait until 90% do so?
Solution :

 Question
26. Under certain circumstances, a nucleus can decay by emitting a particle more massive than an α-particle. Consider the following decay processes:
Question
26. Under certain circumstances, a nucleus can decay by emitting a particle more massive than an α-particle. Consider the following decay processes:
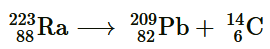
 Calculate the Q-values for these decays and determine that both are energetically allowed.
Solution :
Take a
Calculate the Q-values for these decays and determine that both are energetically allowed.
Solution :
Take a
 emission nuclear reaction:
emission nuclear reaction:
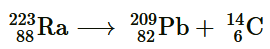 We know that:
Mass of
We know that:
Mass of
 m1 = 223.01850 u
Mass of
m1 = 223.01850 u
Mass of
 m2 = 208.98107 u
Mass of
m2 = 208.98107 u
Mass of
 , m3 = 14.00324 u
Hence, the Q-value of the reaction is given as:
Q = (m1 − m2 − m3) c2
= (223.01850 − 208.98107 − 14.00324) c2
= (0.03419 c2) u
But 1 u = 931.5 MeV/c2
∴Q = 0.03419 × 931.5
= 31.848 MeV
Hence, the Q-value of the nuclear reaction is 31.848 MeV. Since the value is positive, the reaction is energetically allowed.
Now take a
, m3 = 14.00324 u
Hence, the Q-value of the reaction is given as:
Q = (m1 − m2 − m3) c2
= (223.01850 − 208.98107 − 14.00324) c2
= (0.03419 c2) u
But 1 u = 931.5 MeV/c2
∴Q = 0.03419 × 931.5
= 31.848 MeV
Hence, the Q-value of the nuclear reaction is 31.848 MeV. Since the value is positive, the reaction is energetically allowed.
Now take a
 emission nuclear reaction:
emission nuclear reaction:
.png) We know that:
Mass of
We know that:
Mass of
 m1 = 223.01850
Mass of
m1 = 223.01850
Mass of
 m2 = 219.00948
Mass of
m2 = 219.00948
Mass of
 , m3 = 4.00260
Q-value of this nuclear reaction is given as:
Q = (m1 − m2 − m3) c2
= (223.01850 − 219.00948 − 4.00260) C2
= (0.00642 c2) u
= 0.00642 × 931.5 = 5.98 MeV
Hence, the Q value of the second nuclear reaction is 5.98 MeV. Since the value is positive, the reaction is energetically allowed.
Question
27. Consider the fission of
, m3 = 4.00260
Q-value of this nuclear reaction is given as:
Q = (m1 − m2 − m3) c2
= (223.01850 − 219.00948 − 4.00260) C2
= (0.00642 c2) u
= 0.00642 × 931.5 = 5.98 MeV
Hence, the Q value of the second nuclear reaction is 5.98 MeV. Since the value is positive, the reaction is energetically allowed.
Question
27. Consider the fission of
 by fast neutrons. In one fission event, no neutrons are emitted and the final end products, after the beta decay of the primary fragments, are
by fast neutrons. In one fission event, no neutrons are emitted and the final end products, after the beta decay of the primary fragments, are
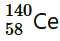 and
and
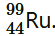 . Calculate Q for this fission process. The relevant atomic and particle masses are
m
. Calculate Q for this fission process. The relevant atomic and particle masses are
m
 =238.05079 u
m
=238.05079 u
m
 =139.90543 u
m
=139.90543 u
m
 = 98.90594 u
Solution :
In the fission of
= 98.90594 u
Solution :
In the fission of
 , 10 β− particles decay from the parent nucleus. The nuclear reaction can be written as:
, 10 β− particles decay from the parent nucleus. The nuclear reaction can be written as:
 It is given that:
Mass of a nucleus
It is given that:
Mass of a nucleus
 m1 = 238.05079 u
Mass of a nucleus
m1 = 238.05079 u
Mass of a nucleus
 m2 = 139.90543 u
Mass of a nucleus
m2 = 139.90543 u
Mass of a nucleus
 , m3 = 98.90594 u
Mass of a neutron
, m3 = 98.90594 u
Mass of a neutron
 m4 = 1.008665 u
Q-value of the above equation,
m4 = 1.008665 u
Q-value of the above equation,
 Where,
m’ = Represents the corresponding atomic masses of the nuclei
Where,
m’ = Represents the corresponding atomic masses of the nuclei
 = m1 − 92me
= m1 − 92me
 = m2 − 58me
= m2 − 58me
 = m3 − 44me
= m3 − 44me
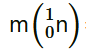 = m4
= m4
 Hence, the Q-value of the fission process is 231.007 MeV.
Question
28. Consider the D−T reaction (deuterium − tritium fusion)
Hence, the Q-value of the fission process is 231.007 MeV.
Question
28. Consider the D−T reaction (deuterium − tritium fusion)
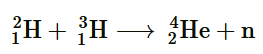 (a) Calculate the energy released in MeV in this reaction from the data:
(a) Calculate the energy released in MeV in this reaction from the data:
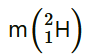 = 2.014102 u
= 2.014102 u
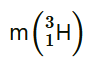 = 3.016049 u
(b)Consider the radius of both deuterium and tritium to be approximately 2.0 fm. What is the kinetic energy needed to overcome the coulomb repulsion between the two nuclei? To what temperature must the gas be heated to initiate the reaction? (Hint: Kinetic energy required for one fusion event =average thermal kinetic energy available with the interacting particles = 2(3kT/2); k = Boltzman’s constant, T = absolute temperature.)
Solution :
(a) Take the D-T nuclear reaction:
= 3.016049 u
(b)Consider the radius of both deuterium and tritium to be approximately 2.0 fm. What is the kinetic energy needed to overcome the coulomb repulsion between the two nuclei? To what temperature must the gas be heated to initiate the reaction? (Hint: Kinetic energy required for one fusion event =average thermal kinetic energy available with the interacting particles = 2(3kT/2); k = Boltzman’s constant, T = absolute temperature.)
Solution :
(a) Take the D-T nuclear reaction:
 It is given that:
Mass of
It is given that:
Mass of
 , m1= 2.014102 u
Mass of
, m1= 2.014102 u
Mass of
 , m2 = 3.016049 u
Mass of
, m2 = 3.016049 u
Mass of
 m3 = 4.002603 u
Mass of
m3 = 4.002603 u
Mass of
 , m4 = 1.008665 u
Q-value of the given D-T reaction is:
Q = [m1 + m2− m3 − m4] c2
= [2.014102 + 3.016049 − 4.002603 − 1.008665] c2
= [0.018883 c2] u
But 1 u = 931.5 MeV/c2
∴Q = 0.018883 × 931.5 = 17.59 MeV
(b) Radius of deuterium and tritium, r ≈ 2.0 fm = 2 × 10−15 m
Distance between the two nuclei at the moment when they touch each other, d = r + r = 4 × 10−15 m
Charge on the deuterium nucleus = e
Charge on the tritium nucleus = e
Hence, the repulsive potential energy between the two nuclei is given as:
, m4 = 1.008665 u
Q-value of the given D-T reaction is:
Q = [m1 + m2− m3 − m4] c2
= [2.014102 + 3.016049 − 4.002603 − 1.008665] c2
= [0.018883 c2] u
But 1 u = 931.5 MeV/c2
∴Q = 0.018883 × 931.5 = 17.59 MeV
(b) Radius of deuterium and tritium, r ≈ 2.0 fm = 2 × 10−15 m
Distance between the two nuclei at the moment when they touch each other, d = r + r = 4 × 10−15 m
Charge on the deuterium nucleus = e
Charge on the tritium nucleus = e
Hence, the repulsive potential energy between the two nuclei is given as:
 Where,
∈0 = Permittivity of free space
Where,
∈0 = Permittivity of free space
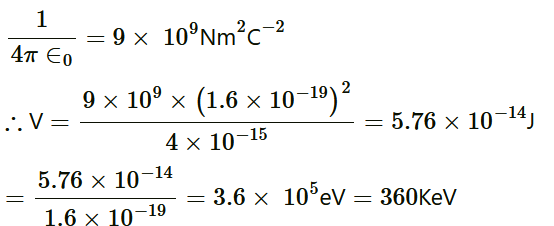 Hence, 5.76 × 10−14 J or
Hence, 5.76 × 10−14 J or
 of kinetic energy (KE) is needed to overcome the Coulomb repulsion between the two nuclei.
However, it is given that:
KE
of kinetic energy (KE) is needed to overcome the Coulomb repulsion between the two nuclei.
However, it is given that:
KE
 Where,
k = Boltzmann constant = 1.38 × 10−23 m2 kg s−2 K−1
T = Temperature required for triggering the reaction
Where,
k = Boltzmann constant = 1.38 × 10−23 m2 kg s−2 K−1
T = Temperature required for triggering the reaction
 Hence, the gas must be heated to a temperature of 1.39 × 109 K to initiate the reaction.
Question
29. Obtain the maximum kinetic energy of β-particles, and the radiation frequencies of γ decays in the decay scheme shown in Fig. 13.6. You are given that
m (198Au) = 197.968233 u
m (198Hg) =197.966760 u
Hence, the gas must be heated to a temperature of 1.39 × 109 K to initiate the reaction.
Question
29. Obtain the maximum kinetic energy of β-particles, and the radiation frequencies of γ decays in the decay scheme shown in Fig. 13.6. You are given that
m (198Au) = 197.968233 u
m (198Hg) =197.966760 u
 Solution :
It can be observed from the given γ-decay diagram that γ1 decays from the 1.088 MeV energy level to the 0 MeV energy level.
Hence, the energy corresponding to γ1-decay is given as:
E1 = 1.088 − 0 = 1.088 MeV
hν1= 1.088 × 1.6 × 10−19 × 106 J
Where,
h = Planck’s constant = 6.6 × 10−34 Js
ν1 = Frequency of radiation radiated by γ1-decay
Solution :
It can be observed from the given γ-decay diagram that γ1 decays from the 1.088 MeV energy level to the 0 MeV energy level.
Hence, the energy corresponding to γ1-decay is given as:
E1 = 1.088 − 0 = 1.088 MeV
hν1= 1.088 × 1.6 × 10−19 × 106 J
Where,
h = Planck’s constant = 6.6 × 10−34 Js
ν1 = Frequency of radiation radiated by γ1-decay
 It can be observed from the given γ-decay diagram that γ2 decays from the 0.412 MeV energy level to the 0 MeV energy level.
Hence, the energy corresponding to γ2-decay is given as:
E2 = 0.412 − 0 = 0.412 MeV
hν2= 0.412 × 1.6 × 10−19 × 106 J
Where,
ν2 = Frequency of radiation radiated by γ2-decay
It can be observed from the given γ-decay diagram that γ2 decays from the 0.412 MeV energy level to the 0 MeV energy level.
Hence, the energy corresponding to γ2-decay is given as:
E2 = 0.412 − 0 = 0.412 MeV
hν2= 0.412 × 1.6 × 10−19 × 106 J
Where,
ν2 = Frequency of radiation radiated by γ2-decay
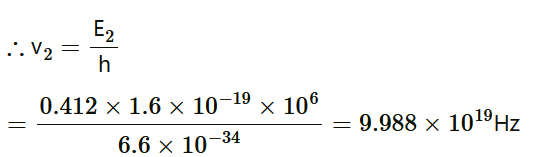 It can be observed from the given γ-decay diagram that γ3 decays from the 1.088 MeV energy level to the 0.412 MeV energy level.
Hence, the energy corresponding to γ3-decay is given as:
E3 = 1.088 − 0.412 = 0.676 MeV
hν3= 0.676 × 10−19 × 106 J
Where,
ν3 = Frequency of radiation radiated by γ3-decay
It can be observed from the given γ-decay diagram that γ3 decays from the 1.088 MeV energy level to the 0.412 MeV energy level.
Hence, the energy corresponding to γ3-decay is given as:
E3 = 1.088 − 0.412 = 0.676 MeV
hν3= 0.676 × 10−19 × 106 J
Where,
ν3 = Frequency of radiation radiated by γ3-decay
.png) Mass of
Mass of
 = 197.968233 u
Mass of
= 197.968233 u
Mass of
 = 197.966760 u
1 u = 931.5 MeV/c2
Energy of the highest level is given as:
= 197.966760 u
1 u = 931.5 MeV/c2
Energy of the highest level is given as:
 β1 decays from the 1.3720995 MeV level to the 1.088 MeV level
∴Maximum kinetic energy of the β1 particle = 1.3720995 − 1.088
= 0.2840995 MeV
β2 decays from the 1.3720995 MeV level to the 0.412 MeV level
∴Maximum kinetic energy of the β2 particle = 1.3720995 − 0.412
= 0.9600995 MeV
Question
30. Calculate and compare the energy released by a) fusion of 1.0 kg of hydrogen deep within Sun and b) the fission of 1.0 kg of 235U in a fission reactor.
Solution :
(a) Amount of hydrogen, m = 1 kg = 1000 g
1 mole, i.e., 1 g of hydrogen
β1 decays from the 1.3720995 MeV level to the 1.088 MeV level
∴Maximum kinetic energy of the β1 particle = 1.3720995 − 1.088
= 0.2840995 MeV
β2 decays from the 1.3720995 MeV level to the 0.412 MeV level
∴Maximum kinetic energy of the β2 particle = 1.3720995 − 0.412
= 0.9600995 MeV
Question
30. Calculate and compare the energy released by a) fusion of 1.0 kg of hydrogen deep within Sun and b) the fission of 1.0 kg of 235U in a fission reactor.
Solution :
(a) Amount of hydrogen, m = 1 kg = 1000 g
1 mole, i.e., 1 g of hydrogen
 contains 6.023 × 1023 atoms.
∴1000 g of
contains 6.023 × 1023 atoms.
∴1000 g of
 contains 6.023 × 1023 × 1000 atoms.
Within the sun, four
contains 6.023 × 1023 × 1000 atoms.
Within the sun, four
 nuclei combine and form one
nuclei combine and form one
 nucleus. In this process 26 MeV of energy is released.
Hence, the energy released from the fusion of 1 kg
nucleus. In this process 26 MeV of energy is released.
Hence, the energy released from the fusion of 1 kg
 is:
is:
 (b) Amount of
(b) Amount of
 = 1 kg = 1000 g
1 mole, i.e., 235 g of
= 1 kg = 1000 g
1 mole, i.e., 235 g of
 contains 6.023 × 1023 atoms.
∴1000 g of
contains 6.023 × 1023 atoms.
∴1000 g of
 contains
contains
 It is known that the amount of energy released in the fission of one atom of
It is known that the amount of energy released in the fission of one atom of
 is 200 MeV.
Hence, energy released from the fission of 1 kg of
is 200 MeV.
Hence, energy released from the fission of 1 kg of
 is:
is:
 Therefore, the energy released in the fusion of 1 kg of hydrogen is nearly 8 times the energy released in the fission of 1 kg of uranium.
Question
31. Suppose India had a target of producing by 2020 AD, 200,000 MW of electric power, ten percent of which was to be obtained from nuclear power plants. Suppose we are given that, on an average, the efficiency of utilization (i.e. conversion to electric energy) of thermal energy produced in a reactor was 25%. How much amount of fissionable uranium would our country need per year by 2020? Take the heat energy per fission of 235U to be about 200MeV.
Solution :
Amount of electric power to be generated, P = 2 × 105 MW
10% of this amount has to be obtained from nuclear power plants.
∴Amount of nuclear power,
Therefore, the energy released in the fusion of 1 kg of hydrogen is nearly 8 times the energy released in the fission of 1 kg of uranium.
Question
31. Suppose India had a target of producing by 2020 AD, 200,000 MW of electric power, ten percent of which was to be obtained from nuclear power plants. Suppose we are given that, on an average, the efficiency of utilization (i.e. conversion to electric energy) of thermal energy produced in a reactor was 25%. How much amount of fissionable uranium would our country need per year by 2020? Take the heat energy per fission of 235U to be about 200MeV.
Solution :
Amount of electric power to be generated, P = 2 × 105 MW
10% of this amount has to be obtained from nuclear power plants.
∴Amount of nuclear power,
 = 2 × 104 MW
= 2 × 104 × 106 J/s
= 2 × 1010 × 60 × 60 × 24 × 365 J/y
Heat energy released per fission of a 235U nucleus, E = 200 MeV
Efficiency of a reactor = 25%
Hence, the amount of energy converted into the electrical energy per fission is calculated as:
= 2 × 104 MW
= 2 × 104 × 106 J/s
= 2 × 1010 × 60 × 60 × 24 × 365 J/y
Heat energy released per fission of a 235U nucleus, E = 200 MeV
Efficiency of a reactor = 25%
Hence, the amount of energy converted into the electrical energy per fission is calculated as:
 Number of atoms required for fission per year:
Number of atoms required for fission per year:
 1 mole, i.e., 235 g of U235 contains 6.023 × 1023 atoms.
∴Mass of 6.023 × 1023 atoms of U235 = 235 g = 235 × 10−3 kg
∴Mass of 78840 × 1024 atoms of U235
1 mole, i.e., 235 g of U235 contains 6.023 × 1023 atoms.
∴Mass of 6.023 × 1023 atoms of U235 = 235 g = 235 × 10−3 kg
∴Mass of 78840 × 1024 atoms of U235

 Hence, the mass of uranium needed per year is 3.076 × 104 kg.
Hence, the mass of uranium needed per year is 3.076 × 104 kg.
NCERT Solutions For Class 12 Physics Chapter 13 FAQs
What is the theory of nuclei Class 12?
Is nuclei a hard chapter?
What are nuclei made of?
What is the model of nuclei?
What are the basics of nuclei?










