Physics Wallah

RD Sharma Solutions Class 9 Maths Chapter 4 Algebraic Identities

Mathematics holds significant importance for students in CBSE Class 9, shaping their academic journey. To ensure students are well-prepared, we provide comprehensive support. In this article, students can access RD Sharma Class 9 Solutions for Maths Chapter 4.
authorImageAnanya Gupta6 Apr, 2024
Share

Share

RD Sharma Solutions Class 9 Maths Chapter 4

RD Sharma Solutions Class 9 Maths Chapter 4: In RD Sharma Class 9 Maths Chapter 4, you'll find solutions for algebraic identities. These solutions help explain the problems in the textbook. They make it easier to understand algebraic equations that are always true, no matter the values of the variables. By using these solutions, you can better understand algebraic concepts and how to solve related math problems. They're designed to be easy to follow and help you prepare well for exams.

By using RD Sharma Class 9 Solutions, students can practice important questions for their final exams, improve time management, and enhance logical thinking skills. These solutions are created by experts at Physics Wallah to help students understand concepts easily. They are available in PDF format for easy access both online and offline.

CBSE Class 9 Science Syllabus 2024-25

RD Sharma Solutions Class 9 Maths Chapter 4 Algebraic Identities PDF

Here we have provided RD Sharma Class 9 Solutions Maths Chapter 4 solutions for the students to help them ace their examinations. Students can refer to these solutions and practice these questions to score better in the exams.

RD Sharma Solutions Class 9 Maths Chapter 4 PDF

RD Sharma Solutions Class 9 Maths Chapter 4 Algebraic Identities

RD Sharma Solutions Class 9 Maths Chapter 4 Algebraic Identities Exercise 4.1 Page No: 4.6

Question 1: Evaluate each of the following using identities:

(i) (2x – 1/x) 2

(ii) (2x + y) (2x – y)

(iii) (a 2 b – b 2 a) 2

(iv) (a – 0.1) (a + 0.1)

(v) (1.5.x 2 – 0.3y 2 ) (1.5x 2 + 0.3y 2 )

Solution :

(i) (2x – 1/x) 2

[Use identity: (a – b) 2 = a 2 + b 2 – 2ab ] (2x – 1/x) 2 = (2x) 2 + (1/x) 2 – 2 (2x)(1/x) = 4x 2 + 1/x 2 – 4

(ii) (2x + y) (2x – y)

[Use identity: (a – b)(a + b) = a 2 – b 2 ] (2x + y) (2x – y) = (2x ) 2 – (y) 2 = 4x 2 – y 2

(iii) (a 2 b – b 2 a) 2

[Use identity: (a – b) 2 = a 2 + b 2 – 2ab ] (a 2 b – b 2 a) 2 = (a 2 b) 2 + (b 2 a) 2 – 2 (a 2 b)( b 2 a) = a 4 b 2 + b 4 a 2 – 2 a 3 b 3

(iv) (a – 0.1) (a + 0.1)

[Use identity: (a – b)(a + b) = a 2 – b 2 ] (a – 0.1) (a + 0.1) = (a) 2 – (0.1) 2 = (a) 2 – 0.01

(v) (1.5 x 2 – 0.3y 2 ) (1.5 x 2 + 0.3y 2 )

[Use identity: (a – b)(a + b) = a 2 – b 2 ] (1.5 x 2 – 0.3y 2 ) (1.5x 2 + 0.3y 2 ) = (1.5 x 2 ) 2 – (0.3y 2 ) 2 = 2.25 x 4 – 0.09y 4

CBSE Class 10 Result 2024 Expected To Be Out Soon

Question 2: Evaluate each of the following using identities:

(i) (399) 2

(ii) (0.98) 2

(iii) 991 x 1009

(iv) 117 x 83

Solution :

(i)

RD sharma class 9 maths chapter 4 ex 4.1 question 2 part 1 Solution

(ii)

RD sharma class 9 maths chapter 4 ex 4.1 question 2 part 2 Solution

(iii)

RD sharma class 9 maths chapter 4 ex 4.1 question 2 part 3 Solution

(iv)

RD sharma class 9 maths chapter 4 ex 4.1 question 2 part 4 Solution

Question 3: Simplify each of the following:

(i) 175 x 175 +2 x 175 x 25 + 25 x 25

(ii) 322 x 322 – 2 x 322 x 22 + 22 x 22

(iii) 0.76 x 0.76 + 2 x 0.76 x 0.24 + 0.24 x 0.24

(iv)

RD sharma class 9 maths chapter 4 ex 4.1 question 3

Solution :

(i) 175 x 175 +2 x 175 x 25 + 25 x 25 = (175) 2 + 2 (175) (25) + (25) 2

= (175 + 25) 2 [Because a 2 + b 2 +2ab = (a+b) 2 ] = (200) 2 = 40000 So, 175 x 175 +2 x 175 x 25 + 25 x 25 = 40000.

(ii) 322 x 322 – 2 x 322 x 22 + 22 x 22

= (322) 2 – 2 x 322 x 22 + (22) 2 = (322 – 22) 2 [Because a 2 + b 2 -2ab = (a-b) 2 ] = (300) 2 = 90000 So, 322 x 322 – 2 x 322 x 22 + 22 x 22= 90000.

(iii) 0.76 x 0.76 + 2 x 0.76 x 0.24 + 0.24 x 0.24

= (0.76) 2 + 2 x 0.76 x 0.24 + (0.24) 2 = (0.76+0.24) 2 [ Because a 2 + b 2 +2ab = (a+b) 2 ] = (1.00) 2 = 1 So, 0.76 x 0.76 + 2 x 0.76 x 0.24 + 0.24 x 0.24 = 1.

(iv)

RD sharma class 9 maths chapter 4 ex 4.1 question 3 part 4 solution

Question 4: If x + 1/x = 11, find the value of x 2 +1/x 2 .

Solution:

RD sharma class 9 maths chapter 4 ex 4.1 question 4

Question 5: If x – 1/x = -1, find the value of x 2 +1/x 2 .

Solution:

RD sharma class 9 maths chapter 4 ex 4.1 question 5 solution

Chapter-wise Solutions for RD Sharma Class 9
RD Sharma Class 9 Solutions Maths
RD Sharma Class 9 Solutions Maths Chapter 1
RD Sharma Class 9 Solutions Maths Chapter 2
RD Sharma Class 9 Solutions Maths Chapter 3
RD Sharma Class 9 Solutions Maths Chapter 5
RD Sharma Class 9 Solutions Maths Chapter 6
RD Sharma Class 9 Solutions Maths Chapter 7
RD Sharma Class 9 Solutions Maths Chapter 8
RD Sharma Class 9 Solutions Maths Chapter 9
RD Sharma Class 9 Solutions Maths Chapter 10
RD Sharma Class 9 Solutions Maths Chapter 11
RD Sharma Class 9 Solutions Maths Chapter 12
RD Sharma Class 9 Solutions Maths Chapter 13
RD Sharma Class 9 Solutions Maths Chapter 14
RD Sharma Class 9 Solutions Maths Chapter 15
RD Sharma Class 9 Solutions Maths Chapter 16
RD Sharma Class 9 Solutions Maths Chapter 17
RD Sharma Class 9 Solutions Maths Chapter 18
RD Sharma Class 9 Solutions Maths Chapter 19
RD Sharma Class 9 Solutions Maths Chapter 20
RD Sharma Class 9 Solutions Maths Chapter 21
RD Sharma Class 9 Solutions Maths Chapter 22
RD Sharma Class 9 Solutions Maths Chapter 23
RD Sharma Class 9 Solutions Maths Chapter 24
RD Sharma Class 9 Solutions Maths Chapter 25

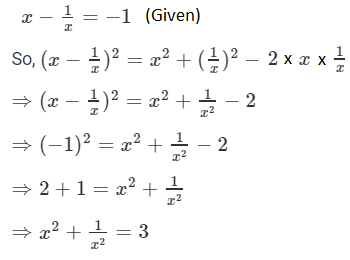
RD Sharma Solutions Class 9 Maths Chapter 4 Algebraic Identities Exercise 4.2 Page No: 4.11

Question 1: Write the following in the expanded form:

(i) (a + 2b + c) 2

(ii) (2a − 3b − c) 2

(iii) (−3x+y+z) 2

(iv) (m+2n−5p) 2

(v) (2+x−2y) 2

(vi) (a 2 +b 2 +c 2 ) 2

(vii) (ab+bc+ca) 2

(viii) (x/y+y/z+z/x)2

(ix) (a/bc + b/ac + c/ab) 2

(x) (x+2y+4z) 2

(xi) (2x−y+z) 2

(xii) (−2x+3y+2z) 2

Solution :

Using identities: (x + y + z) 2 = x 2 + y 2 + z 2 + 2xy + 2yz + 2xz

(i) (a + 2b + c) 2

= a 2 + (2b) 2 + c 2 + 2a(2b) + 2ac + 2(2b)c = a 2 + 4b 2 + c 2 + 4ab + 2ac + 4bc

(ii) (2a − 3b − c) 2

= [(2a) + (−3b) + (−c)] 2 = (2a) 2 + (−3b) 2 + (−c) 2 + 2(2a)(−3b) + 2(−3b)(−c) + 2(2a)(−c) = 4a 2 + 9b 2 + c 2 − 12ab + 6bc − 4ca

(iii) (−3x+y+z) 2

= [(−3x) 2 + y 2 + z 2 + 2(−3x)y + 2yz + 2(−3x)z = 9x 2 + y 2 + z 2 − 6xy + 2yz − 6xz

(iv) (m+2n−5p) 2

= m 2 + (2n) 2 + (−5p) 2 + 2m × 2n + (2×2n×−5p) + 2m × −5p = m 2 + 4n 2 + 25p 2 + 4mn − 20np − 10pm

(v) (2+x−2y) 2

= 2 2 + x 2 + (−2y) 2 + 2(2)(x) + 2(x)(−2y) + 2(2)(−2y) = 4 + x 2 + 4y 2 + 4 x − 4xy − 8y

(vi) (a 2 +b 2 +c 2 ) 2

= (a 2 ) 2 + (b 2 ) 2 + (c 2 ) 2 + 2a 2 b 2 + 2b 2 c 2 + 2a 2 c 2 = a 4 + b 4 + c 4 + 2a 2 b 2 + 2b 2 c 2 + 2c 2 a 2

(vii) (ab+bc+ca) 2

= (ab) 2 + (bc) 2 + (ca) 2 + 2(ab)(bc) + 2(bc)(ca) + 2(ab)(ca) = a 2 b 2 + b 2 c 2 + c 2 a 2 + 2(ac)b 2 + 2(ab)(c) 2 + 2(bc)(a) 2

(viii) (x/y+y/z+z/x) 2

RD sharma class 9 maths chapter 4 ex 4.2 question 1 solution

(ix) (a/bc + b/ac + c/ab) 2

RD sharma class 9 maths chapter 4 ex 4.2 question 1 solution

(x) (x+2y+4z) 2

= x 2 + (2y) 2 + (4z) 2 + (2x)(2y) + 2(2y)(4z) + 2x(4z) = x 2 + 4y 2 + 16z 2 + 4xy + 16yz + 8xz

(xi) (2x−y+z) 2

= (2x) 2 + (−y) 2 + (z) 2 + 2(2x)(−y) + 2(−y)(z) + 2(2x)(z) = 4x 2 + y 2 + z 2 − 4xy−2yz+4xz

(xii) (−2x+3y+2z) 2

= (−2x) 2 + (3y) 2 + ( 2z) 2 + 2(−2x)(3y)+2(3y)(2z)+2(−2x)(2z) = 4x 2 + 9y 2 + 4z 2 −12xy+12yz−8xz

Question 2: Simplify

(i) (a + b + c) 2 + (a − b + c) 2

(ii) (a + b + c) 2 − (a − b + c) 2

(iii) (a + b + c) 2 + (a – b + c) 2 + (a + b − c) 2

(iv) (2x + p − c) 2 − (2x − p + c) 2

(v) (x 2 + y 2 − z 2 ) 2 − (x 2 − y 2 + z 2 ) 2

Solution:

(i) (a + b + c) 2 + (a − b + c) 2

= (a 2 + b 2 + c 2 + 2ab+2bc+2ca) + (a 2 + (−b) 2 + c 2 −2ab−2bc+2ca) = 2a 2 + 2 b 2 + 2c 2 + 4ca

(ii) (a + b + c) 2 − (a − b + c) 2

= (a 2 + b 2 + c 2 + 2ab+2bc+2ca) − (a 2 + (−b) 2 + c 2 −2ab−2bc+2ca) = a 2 + b 2 + c 2 + 2ab + 2bc + 2ca − a 2 − b 2 − c 2 + 2ab + 2bc − 2ca = 4ab + 4bc

(iii) (a + b + c) 2 + (a – b + c) 2 + (a + b − c) 2

= a 2 + b 2 + c 2 + 2ab + 2bc + 2ca + (a 2 + b 2 + (c) 2 − 2ab − 2cb + 2ca) + (a 2 + b 2 + c 2 + 2ab − 2bc – 2ca) = 3 a 2 + 3b 2 + 3c 2 + 2ab − 2bc + 2ca

(iv) (2x + p − c) 2 − (2x − p + c) 2

= [4x 2 + p 2 + c 2 + 4xp − 2pc − 4xc] − [4x 2 + p 2 + c 2 − 4xp− 2pc + 4xc] = 4x 2 + p 2 + c 2 + 4xp − 2pc − 4cx − 4x 2 − p 2 − c 2 + 4xp + 2pc− 4cx = 8xp − 8xc = 8(xp − xc)

(v) (x 2 + y 2 − z 2 ) 2 − (x 2 − y 2 + z 2 ) 2

= (x 2 + y 2 + (−z) 2 ) 2 − (x 2 − y 2 + z 2 ) 2 = [x 4 + y 4 + z 4 + 2x 2 y 2 – 2y 2 z 2 – 2x 2 z 2 − [x 4 + y 4 + z 4 − 2x 2 y 2 − 2y 2 z 2 + 2x 2 z 2 ] = 4x 2 y 2 – 4z 2 x 2

Question 3: If a + b + c = 0 and a 2 + b 2 + c 2 = 16, find the value of ab + bc + ca.

Solution :

a + b + c = 0 and a 2 + b 2 + c 2 = 16 (given) Choose a + b + c = 0 Squaring both sides, (a + b + c) 2 = 0 a 2 + b 2 + c 2 + 2(ab + bc + ca) = 0 16 + 2(ab + bc + c) = 0 2(ab + bc + ca) = -16 ab + bc + ca = -16/2 = -8 or ab + bc + ca = -8

RD Sharma Solutions Class 9 Maths Chapter 4 Algebraic Identities Exercise 4.3 Page No: 4.19

Question 1: Find the cube of each of the following binomial expressions:

(i) (1/x + y/3)

(ii) (3/x – 2/x 2 )

(iii) (2x + 3/x)

(iv) (4 – 1/3x)

Solution:

[Using identities: (a + b) 3 = a 3 + b 3 + 3ab(a + b) and (a – b) 3 = a 3 – b 3 – 3ab(a – b) ]

(i)

RD sharma class 9 maths chapter 4 ex 4.3 Q1 part 1 solution

(ii)

RD sharma class 9 maths chapter 4 ex 4.3 Q1 part 2 solution

(iii)

RD sharma class 9 maths chapter 4 ex 4.3 Q1 part 3 solution

(iv)

RD sharma class 9 maths chapter 4 ex 4.3 Q1 part 4 solution

Question 2: Simplify each of the following:

(i) (x + 3) 3 + (x – 3) 3

(ii) (x/2 + y/3) 3 – (x/2 – y/3) 3

(iii) (x + 2/x) 3 + (x – 2/x) 3

(iv) (2x – 5y) 3 – (2x + 5y) 3

Solution:

[Using identities: a 3 + b 3 = (a + b)(a 2 + b 2 – ab) a 3 – b 3 = (a – b)(a 2 + b 2 + ab) (a + b)(a-b) = a 2 – b 2 (a + b) 2 = a 2 + b 2 + 2ab and (a – b) 2 = a 2 + b 2 – 2ab]

(i) (x + 3) 3 + (x – 3) 3

Here a = (x + 3), b = (x – 3) RD sharma class 9 maths chapter 4 ex 4.3 Q2 solution part 1

(ii) (x/2 + y/3) 3 – (x/2 – y/3) 3

Here a = (x/2 + y/3) and b = (x/2 – y/3) RD sharma class 9 maths chapter 4 ex 4.3 Q2 solution part 2

(iii) (x + 2/x) 3 + (x – 2/x) 3

Here a = (x + 2/x) and b = (x – 2/x) RD sharma class 9 maths chapter 4 ex 4.3 Q2 solution part 3

(iv) (2x – 5y) 3 – (2x + 5y) 3

Here a = (2x – 5y) and b = 2x + 5y RD sharma class 9 maths chapter 4 ex 4.3 Q2 solution part 4

Question 3: If a + b = 10 and ab = 21, find the value of a 3 + b 3 .

Solution :

a + b = 10, ab = 21 (given) Choose a + b = 10 Cubing both sides, (a + b) 3 = (10) 3 a 3 + b 3 + 3ab(a + b) = 1000 a 3 + b 3 + 3 x 21 x 10 = 1000 (using given values) a 3 + b 3 + 630 = 1000 a 3 + b 3 = 1000 – 630 = 370 or a 3 + b 3 = 370

Question 4: If a – b = 4 and ab = 21, find the value of a 3 – b 3 .

Solution :

a – b = 4, ab= 21 (given) Choose a – b = 4 Cubing both sides, (a – b) 3 = (4) 3 a 3 – b 3 – 3ab (a – b) = 64 a 3 – b 3 – 3 × 21 x 4 = 64 (using given values) a 3 – b 3 – 252 = 64 a 3 – b 3 = 64 + 252 = 316 Or a 3 – b 3 = 316

Question 5: If x + 1/x = 5, find the value of x 3 + 1/x 3 .

Solution :

Given: x + 1/x = 5 Apply Cube on x + 1/x RD sharma class 9 maths chapter 4 ex 4.3 Q5 solution

Question 6: If x – 1/x = 7, find the value of x 3 – 1/x 3 .

Solution :

Given: x – 1/x = 7 Apply Cube on x – 1/x RD sharma class 9 maths chapter 4 ex 4.3 Q6 solution

Question 7: If x – 1/x = 5, find the value of x 3 – 1/x 3 .

Solution:

Given: x – 1/x = 5 Apply Cube on x – 1/x

RD sharma class 9 maths chapter 4 ex 4.3 Ques 7 solution

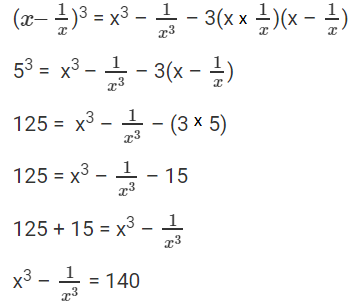
Question 8: If (x 2 + 1/x 2 ) = 51, find the value of x 3 – 1/x 3 .

Solution:

We know that: (x – y) 2 = x 2 + y 2 – 2xy Replace y with 1/x, we get (x – 1/x) 2 = x 2 + 1/x 2 – 2 Since (x 2 + 1/x 2 ) = 51 (given) (x – 1/x) 2 = 51 – 2 = 49 or (x – 1/x) = ±7 Now, Find x 3 – 1/x 3 We know that, x 3 – y 3 = (x – y)(x 2 + y 2 + xy) Replace y with 1/x, we get x 3 – 1/x 3 = (x – 1/x)(x 2 + 1/x 2 + 1) Use (x – 1/x) = 7 and (x 2 + 1/x 2 ) = 51 x 3 – 1/x 3 = 7 x 52 = 364 x 3 – 1/x 3 = 364

Question 9: If (x 2 + 1/x 2 ) = 98, find the value of x 3 + 1/x 3 .

Solution:

We know that: (x + y) 2 = x 2 + y 2 + 2xy Replace y with 1/x, we get (x + 1/x) 2 = x 2 + 1/x 2 + 2 Since (x 2 + 1/x 2 ) = 98 (given) (x + 1/x) 2 = 98 + 2 = 100 or (x + 1/x) = ±10 Now, Find x 3 + 1/x 3 We know that, x 3 + y 3 = (x + y)(x 2 + y 2 – xy) Replace y with 1/x, we get x 3 + 1/x 3 = (x + 1/x)(x 2 + 1/x 2 – 1) Use (x + 1/x) = 10 and (x 2 + 1/x 2 ) = 98 x 3 + 1/x 3 = 10 x 97 = 970 x 3 + 1/x 3 = 970

Question 10: If 2x + 3y = 13 and xy = 6, find the value of 8x 3 + 27y 3 .

Solution:

Given: 2x + 3y = 13, xy = 6 Cubing 2x + 3y = 13 both sides, we get (2x + 3y) 3 = (13) 3 (2x) 3 + (3y) 3 + 3( 2x )(3y) (2x + 3y) = 2197 8x 3 + 27y 3 + 18xy(2x + 3y) = 2197 8x 3 + 27y 3 + 18 x 6 x 13 = 2197 8x 3 + 27y 3 + 1404 = 2197 8x 3 + 27y 3 = 2197 – 1404 = 793 8x 3 + 27y 3 = 793

Question 11: If 3x – 2y= 11 and xy = 12, find the value of 27x 3 – 8y 3 .

Solution:

Given: 3x – 2y = 11 and xy = 12 Cubing 3x – 2y = 11 both sides, we get (3x – 2y) 3 = (11) 3 (3x) 3 – (2y) 3 – 3 ( 3x)( 2y) (3x – 2y) =1331 27x 3 – 8y 3 – 18xy(3x -2y) =1331 27x 3 – 8y 3 – 18 x 12 x 11 = 1331 27x 3 – 8y 3 – 2376 = 1331 27x 3 – 8y 3 = 1331 + 2376 = 3707 27x 3 – 8y 3 = 3707

RD Sharma Solutions Class 9 Maths Chapter 4 Algebraic Identities Exercise 4.4 Page No: 4.23

Question 1: Find the following products:

(i) (3x + 2y)(9x 2 – 6xy + 4y 2 )

(ii) (4x – 5y)(16x 2 + 20xy + 25y 2 )

(iii) (7p 4 + q)(49p 8 – 7p 4 q + q 2 )

(iv) (x/2 + 2y)(x 2 /4 – xy + 4y 2 )

(v) (3/x – 5/y)(9/x 2 + 25/y 2 + 15/xy)

(vi) (3 + 5/x)(9 – 15/x + 25/x 2 )

(vii) (2/x + 3x)(4/x 2 + 9x 2 – 6)

(viii) (3/x – 2x 2 )(9/x 2 + 4x 4 – 6x)

(ix) (1 – x)(1 + x + x 2 )

(x) (1 + x)(1 – x + x 2 )

(xi) (x 2 – 1)(x 4 + x 2 +1)

(xii) (x 3 + 1)(x 6 – x 3 + 1)

Solution:

(i) (3x + 2y)(9x 2 – 6xy + 4y 2 )

= (3x + 2y)[(3x) 2 – (3x)(2y) + (2y) 2 )] We know, a 3 + b 3 = (a + b)(a 2 + b 2 – ab) = (3x) 3 + (2y) 3 = 27x 3 + 8y 3

(ii) (4x – 5y)(16x 2 + 20xy + 25y 2 )

= (4x – 5y)[(4x) 2 + (4x)(5y) + (5y) 2 )] We know, a 3 – b 3 = (a – b)(a 2 + b 2 + ab) = (4x) 3 – (5y) 3 = 64x 3 – 125y 3

(iii) (7p 4 + q)(49p 8 – 7p 4 q + q 2 )

= (7p 4 + q)[(7p 4 ) 2 – (7p 4 )(q) + (q) 2 )] We know, a 3 + b 3 = (a + b)(a 2 + b 2 – ab) = (7p 4 ) 3 + (q) 3 = 343 p 12 + q 3

(iv) (x/2 + 2y)(x 2 /4 – xy + 4y 2 )

We know, a 3 – b 3 = (a – b)(a 2 + b 2 + ab) (x/2 + 2y)(x 2 /4 – xy + 4y 2 ) RD sharma class 9 maths chapter 4 ex 4.4 question 2 Solution

(v) (3/x – 5/y)(9/x 2 + 25/y 2 + 15/xy)

RD sharma class 9 maths chapter 4 ex 4.4 [Using a 3 – b 3 = (a – b)(a 2 + b 2 + ab) ]

(vi) (3 + 5/x)(9 – 15/x + 25/x 2 )

RD sharma class 9 maths chapter 4 ex 4.4 solution [Using: a 3 + b 3 = (a + b)(a 2 + b 2 – ab)]

(vii) (2/x + 3x)(4/x 2 + 9x 2 – 6)

RD sharma class 9 maths chapter 4 ex 4.4 question 1 [Using: a 3 + b 3 = (a + b)(a 2 + b 2 – ab)]

(viii) (3/x – 2x 2 )(9/x 2 + 4x 4 – 6x)

RD sharma class 9 maths chapter 4 ex 4.4 question 1 solution [Using : a 3 – b 3 = (a – b)(a 2 + b 2 + ab)]

(ix) (1 – x)(1 + x + x 2 )

And we know, a 3 – b 3 = (a – b)(a 2 + b 2 + ab) (1 – x)(1 + x + x 2 ) can be written as (1 – x)[(1 2 + (1)(x)+ x 2 )] = (1) 3 – (x) 3 = 1 – x 3

(x) (1 + x)(1 – x + x 2 )

And we know, a 3 + b 3 = (a + b)(a 2 + b 2 – ab)] (1 + x)(1 – x + x 2 ) can be written as, (1 + x)[(1 2 – (1)(x) + x 2 )] = (1) 3 + (x) 3 = 1 + x 3

(xi) (x 2 – 1)(x 4 + x 2 +1) can be written as,

(x 2 – 1)[(x 2 ) 2 – 1 2 + (x 2 )(1)] = (x 2 ) 3 – 1 3 = x 6 – 1 [using a 3 – b 3 = (a – b)(a 2 + b 2 + ab) ]

(xii) (x 3 + 1)(x 6 – x 3 + 1) can be written as,

(x 3 + 1)[(x 3 ) 2 – (x 3 )(1) + 1 2 ] = (x 3 ) 3 + 1 3 = x 9 + 1 [using a 3 + b 3 = (a + b)(a 2 + b 2 – ab) ]

Question 2: If x = 3 and y = -1, find the values of each of the following using in identity:

(i) (9y 2 – 4x 2 )(81y 4 + 36x 2 y 2 + 16x 4 )

(ii) (3/x – x/3)(x 2 /9 + 9/x 2 + 1)

(iii) (x/7 + y/3)(x 2 /49 + y 2 /9 – xy/21)

(iv) (x/4 – y/3)(x 2 /16 + xy/12 + y 2 /9) (v) (5/x + 5x)(25/x 2 – 25 + 25x 2 )

Solution:

(i) (9y 2 – 4x 2 )(81y 4 + 36x 2 y 2 + 16x 4 )

= (9y 2 – 4x 2 ) [(9y 2 ) 2 + 9y 2 x 4x 2 + (4x 2 ) 2 ] = (9y 2 ) 3 – (4x 2 ) 3 = 729 y 6 – 64 x 6 Put x = 3 and y = -1 = 729 – 46656 = – 45927

(ii) Put x = 3 and y = -1

(3/x – x/3)(x 2 /9 + 9/x 2 + 1) RD sharma class 9 maths chapter 4 ex 4.4 question 2 solution part 2

(iii) Put x = 3 and y = -1

(x/7 + y/3)(x 2 /49 + y 2 /9 – xy/21) RD sharma class 9 maths chapter 4 ex 4.4 question 2 solution part 3

(iv) Put x = 3 and y = -1

(x/4 – y/3)(x 2 /16 + xy/12 + y 2 /9) RD sharma class 9 maths chapter 4 ex 4.4 question 2 solution part 4

(v) Put x = 3 and y = -1

(5/x + 5x)(25/x 2 – 25 + 25x 2 )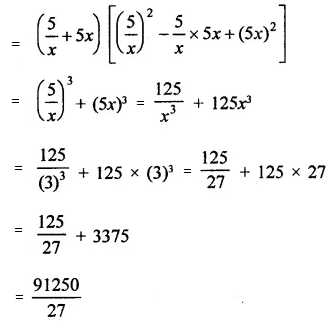 RD sharma class 9 maths chapter 4 ex 4.4 question 2 solution part 5

Question 3: If a + b = 10 and ab = 16, find the value of a 2 – ab + b 2 and a 2 + ab + b 2 .

Solution:

a + b = 10, ab = 16 Squaring, a + b = 10, both sides (a + b) 2 = (10) 2 a 2 + b 2 + 2ab = 100 a 2 + b 2 + 2 x 16 = 100 a 2 + b 2 + 32 = 100 a 2 + b 2 = 100 – 32 = 68 a 2 + b 2 = 68 Again, a 2 – ab + b 2 = a 2 + b 2 – ab = 68 – 16 = 52 and a 2 + ab + b 2 = a 2 + b 2 + ab = 68 + 16 = 84

Question 4: If a + b = 8 and ab = 6, find the value of a 3 + b 3 .

Solution:

a + b = 8, ab = 6 Cubing, a + b = 8, both sides, we get (a + b) 3 = (8) 3 a 3 + b 3 + 3ab(a + b) = 512 a 3 + b 3 + 3 x 6 x 8 = 512 a 3 + b 3 + 144 = 512 a 3 + b 3 = 512 – 144 = 368 a 3 + b 3 = 368

RD Sharma Class 9 Solutions Maths Chapter 4 Algebraic Identities Exercise 4.5 Page No: 4.28

Question 1: Find the following products:

(i) (3x + 2y + 2z) (9x 2 + 4y 2 + 4z 2 – 6xy – 4yz – 6zx)

(ii) (4x – 3y + 2z) (16x 2 + 9y 2 + 4z 2 + 12xy + 6yz – 8zx)

(iii) (2a – 3b – 2c) (4a 2 + 9b 2 + 4c 2 + 6ab – 6bc + 4ca)

(iv) (3x -4y + 5z) (9x 2 + 16y 2 + 25z 2 + 12xy- 15zx + 20yz)

Solution:

(i) (3x + 2y + 2z) (9x 2 + 4y 2 + 4z 2 – 6xy – 4yz – 6zx)

= (3x + 2y + 2z) [(3x) 2 + (2y) 2 + (2z) 2 – 3x x 2y – 2y x 2z – 2z x 3x] = (3x) 3 + (2y) 3 + (2z) 3 – 3 x 3x x 2y x 2z = 27x 3 + 8y 3 + 8Z 3 – 36xyz

(ii) (4x – 3y + 2z) (16x 2 + 9y 2 + 4z 2 + 12xy + 6yz – 8zx)

= (4x -3y + 2z) [(4x) 2 + (-3y) 2 + (2z) 2 – 4x x (-3y) – (-3y) x (2z) – (2z x 4x)] = (4x) 3 + (-3y) 3 + (2z) 3 – 3 x 4x x (-3y) x (2z) = 64x 3 – 27y 3 + 8z 3 + 72xyz

(iii) (2a -3b- 2c) (4a 2 + 9b 2 + 4c 2 + 6ab – 6bc + 4ca)

= (2a -3b- 2c) [(2a) 2 + (-3b) 2 + (-2c) 2 – 2a x (-3b) – (-3b) x (-2c) – (-2c) x 2a] = (2a) 3 + (-3b) 3 + (-2c) 3 -3x 2a x (-3 b) (-2c) = 8a 3 – 21b 3 – 8c 3 – 36abc

(iv) (3x – 4y + 5z) (9x 2 + 16y 2 + 25z 2 + 12xy – 15zx + 20yz)

= [3x + (-4y) + 5z] [(3x) 2 + (-4y) 2 + (5z) 2 – 3x x (-4y) -(-4y) (5z) – 5z x 3x] = (3x) 3 + (-4y) 3 + (5z) 3 – 3 x 3x x (-4y) (5z) = 27x 3 – 64y 3 + 125z 3 + 180xyz

Question 2: If x + y + z = 8 and xy + yz+ zx = 20, find the value of x 3 + y 3 + z 3 – 3xyz.

Solution:

We know, x 3 + y 3 + z 3 – 3xyz = (x + y + z) (x 2 + y 2 + z 2 – xy – yz – zx) Squaring, x + y + z = 8 both sides, we get (x + y + z) 2 = (8) 2 x 2 + y 2 + z 2 + 2(xy + yz + zx) = 64 x 2 + y 2 + z 2 + 2 x 20 = 64 x 2 + y 2 + z 2 + 40 = 64 x 2 + y 2 + z 2 = 24 Now, x 3 + y 3 + z 3 – 3xyz = (x + y + z) [x 2 + y 2 + z 2 – (xy + yz + zx)] = 8(24 – 20) = 8 x 4 = 32 ⇒ x 3 + y 3 + z 3 – 3xyz = 32

Question 3: If a +b + c = 9 and ab + bc + ca = 26, find the value of a 3 + b 3 + c 3 – 3abc.

Solution:

a + b + c = 9, ab + bc + ca = 26 Squaring, a + b + c = 9 both sides, we get (a + b + c) 2 = (9) 2 a 2 + b 2 + c 2 + 2 (ab + bc + ca) = 81 a 2 + b 2 + c 2 + 2 x 26 = 81 a 2 + b 2 + c 2 + 52 = 81 a 2 + b 2 + c 2 = 29 Now, a 3 + b 3 + c 3 – 3abc = (a + b + c) [(a 2 + b 2 + c 2 – (ab + bc + ca)] = 9[29 – 26] = 9 x 3 = 27 ⇒ a 3 + b 3 + c 3 – 3abc = 27

RD Sharma Class 9 Solutions Maths Chapter 4 Algebraic Identities Exercise VSAQs Page No: 4.28

Question 1: If x + 1/x = 3, then find the value of x 2 + 1/x 2 .

Solution:

x + 1/x = 3 Squaring both sides, we have (x + 1/x) 2 = 3 2 x 2 + 1/x 2 + 2 = 9 x 2 + 1/x 2 = 9 – 2 = 7

Question 2: If x + 1/x = 3, then find the value of x^6 + 1/x^6.

Solution :

x + 1/x = 3 Squaring both sides, we have (x + 1/x) 2 = 3 2 x 2 + 1/x 2 + 2 = 9 x 2 + 1/x 2 = 9 – 2 = 7 x 2 + 1/x 2 = 7 …(1) Cubing equation (1) both sides, RD sharma class 9 maths chapter 4 ex vsaqs solutions

Question 3: If a + b = 7 and ab = 12, find the value of a 2 + b 2 .

Solution:

a + b = 7, ab = 12 Squaring, a + b = 7, both sides, (a + b) 2 = (7) 2 a 2 + b 2 + 2ab = 49 a 2 + b 2 + 2 x 12 = 49 a 2 + b 2 + 24 = 49 a 2 + b 2 = 25

Question 4: If a – b = 5 and ab = 12, find the value of a 2 + b 2 .

Solution:

a – b = 5, ab = 12 Squaring, a – b = 5, both sides, (a – b) 2 = (5) 2 a 2 + b 2 – 2ab = 25 a 2 + b 2 – 2 x 12 = 25 a 2 + b 2 – 24 = 25 a 2 + b 2 = 49
CBSE Class 9 Maths Syllabus CBSE Class 9 Science Syllabus
CBSE Class 9 Computer Application Syllabus CBSE Class 9 Social Science Syllabus

RD Sharma Solutions Class 9 Maths Chapter 4 FAQs

What topics are covered in RD Sharma Class 9 Maths Chapter 4 on Algebraic Identities?

RD Sharma Class 9 Maths Chapter 4 covers various topics related to algebraic identities, including polynomial identities, binomial theorem, and factorization.

How can RD Sharma Solutions help in understanding Algebraic Identities?

RD Sharma Solutions provide step-by-step explanations to problems, helping students understand the concepts better.

How can RD Sharma Solutions benefit students in exams?

By practicing with RD Sharma Solutions, students can improve their problem-solving skills and gain confidence in tackling exam questions. The solutions provide clarity on concepts and help students score well in exams.
Popup Close ImagePopup Open Image
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Popup Image
CTA Image
008448982616
Check out these Related Articles
BlogImage
CLASS 9 EXAM
Share
CBSE Class 9 Maths Notes Chapter 10 Solutions PDF
Read Full Story
11 Sept 2025, 02:17 pm
BlogImage
CLASS 9 EXAM
Share
Iswaran The Storyteller Important Question Answer Class 9 English Moments
Read Full Story
23 Aug 2025, 02:01 pm
BlogImage
CLASS 9 EXAM
Share
The Adventures of Toto Important Questions and Answers PDF Download
Read Full Story
21 Aug 2025, 02:14 pm
BlogImage
CLASS 9 EXAM
Share
The Road Not Taken Important Questions Class 9 English PDF Download
Read Full Story
2 Sept 2025, 01:54 pm
BlogImage
CLASS 9 EXAM
Share
Important Questions for Class 9 English Beehive Chapter 1 PDF Download
Read Full Story
2 Sept 2025, 01:53 pm
BlogImage
CLASS 9 EXAM
Share
Important Questions for Class 9 English Beehive Chapter 4 PDF Download
Read Full Story
26 Aug 2025, 04:17 pm
BlogImage
CLASS 9 EXAM
Share
Important Questions for Class 9 English Beehive Chapter 3 The Little Girl
Read Full Story
26 Aug 2025, 02:14 pm
BlogImage
CLASS 9 EXAM
Share
Important Questions for Class 9 English Beehive Chapter 2 Sound of Music
Read Full Story
25 Aug 2025, 02:44 pm
BlogImage
CLASS 9 EXAM
Share
CBSE Sample Papers Class 9 Social Science 2025-26 PDF with Solutions
Read Full Story
7 Aug 2025, 02:13 pm
Join 15 Million students on the app today!
Point IconLive & recorded classes available at ease
Point IconDashboard for progress tracking
Point IconMillions of practice questions at your fingertips
Download ButtonDownload Button
Banner Image
Banner Image
Free Learning Resources
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Privacy Policy
Terms of use
Copyright © 2025 Physicswallah Limited All rights reserved.