Arc Length Formula: How to Calculate Arc Length Easily

Arc length refers to the measurement of the distance along any part of the circumference of a circle or a curve, commonly referred to as an arc. It represents the total length along the curved line that constitutes the arc. This concept is most commonly associated with circular arcs, but it can apply to any curved shape. It's important to note that the arc's length is invariably greater than the straight-line distance between its two endpoints, known as a chord.

For a circular arc specifically, with a circle of radius 'r' and an angle θ that it subtends at the circle's center, you can calculate the arc length using different formulas based on the unit of angle measurement:

If the angle θ is measured in degrees, the formula for arc length is rθ × (π/180). This formula takes into account the degree measure and converts it into radians by multiplying by π/180.

If the angle θ is measured in radians, then the arc length formula is simpler: rθ. In this case, there's no need for conversion, as the angle is already in radians.

Now, let's explore how these formulas are derived.

What is Arc Length?

The arc length is defined as the interspace between the two points along a section of a curve. An arc of a circle is any part of the circumference. The angle subtended by an arc at any point is the angle formed between the two line segments joining the center to the end-points of the arc. For example, in the circle shown below, OP is the arc of the circle with center Q. The arc length of this arc OP is given as L.

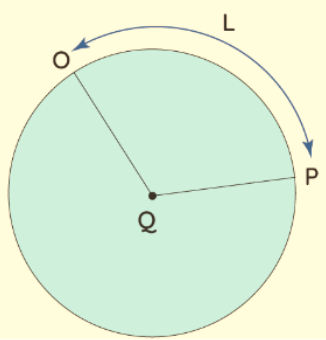
representation of an arc length, arc of a circle

Arc Length Formula

To derive the formula for arc length, let's begin by recalling the circumference of a full circle with a radius 'r,' which is 2πr. Now, consider that an arc represents only a portion (or fraction) of the entire circumference. In a full circle, the central angle is 360 degrees. If an arc subtends an angle of θ degrees, it implies that the arc occupies a fraction of θ/360 out of the total circumference. Therefore:

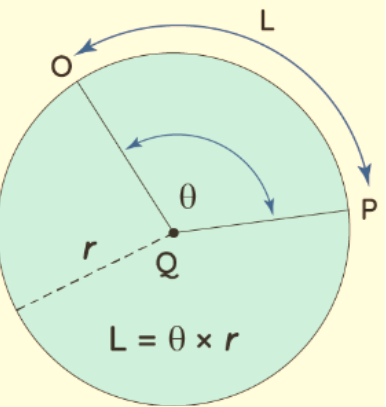
Arc length = (θ/360) of 2πr = (θ/360) × 2πr = rθ × π/180.

This formula represents the arc length when the angle is measured in degrees. The length of an arc can be determined using different formulas, depending on the unit used to measure the central angle. The central angle's measurement can be in degrees or radians, and accordingly, we calculate the arc length of a circle.

If θ is given in radians, we can convert radians to degrees using the formula: angle in degrees = θ × 180/π. Substituting this into the formula above:

Arc length = rθ × π/180 × 180/π = rθ.

Hence, the formula for the arc length of a circle is θ times the radius of the circle when the angle is in radians.

In summary, the arc length formula can be expressed as:

For angles in radians: Arc length, L = θ × r.

For angles in degrees: Arc length, L = θ × (π/180) × r.

Where:

L = Length of an Arc

θ = Central Angle of the Arc

r = Radius of the Circle

Also Check – Line and Angles Formula

Arc Length Formula in Radians

The calculation of the arc length in a circle involves various formulas, depending on the unit of measurement for the central angle of the arc. When expressing the arc length in radians, the formula can be stated as follows:

Arc Length = θ × r

In this equation:

L represents the arc length.

θ denotes the central angle of the arc, measured in radians.

r stands for the radius of the circle.

How to Find Arc Length of a Curve?

The calculation of the arc length for a segment of a circle involves various methods and formulas, depending on the available information. Key scenarios include:

Determining arc length when provided with the radius and central angle.

Calculating arc length without knowledge of the radius.

Finding arc length without information about the central angle.

Let's delve into the process of calculating arc length using the radius and central angle.

Also Check – Line and Angles Formula

How to Find Arc Length With the Radius and Central Angle?

To calculate the arc length of a circle, you can utilize the arc length formula, which depends on whether the central angle is measured in radians or degrees:

When θ is in radians:

Arc Length = θ × r

When θ is in degrees:

Arc Length = θ × (π/180) × r

Also Check – Congruence of triangles formula

How to Find Arc Length Without the Radius?

The arc length of a circle can be determined even without knowing the radius by using different methods based on the information available:

1. Central Angle and Sector Area:

To find the arc length when provided with the central angle and sector area, you can follow these steps:

Utilize the sector area formula, which depends on whether the angle θ is in degrees or radians:

If θ is in degrees: (θ/360º) × πr²

If θ is in radians: (1/2) r²θ

Solve for the radius 'r' by rearranging the formula and taking the square root.

Once you have the radius, use the relevant formula to find the arc length.

Example:

Calculate the arc length of a curve with a sector area of 25 square units and a central angle of 2 radians.

Sector area = 25 units

Central angle = 2 radians

Calculate 'r' using the formula.

Find arc length as rθ.

2. Central Angle and Chord Length:

To determine the arc length when given the central angle and chord length, proceed as follows:

Use the chord length formula: 2r sin(θ/2).

Solve for the radius 'r.'

With the radius in hand, easily calculate the arc length using the appropriate formula.

Example:

Calculate the arc length of a curve when its endpoints touch a chord of the circle, measuring 5 units. The central angle subtended by the arc is 2 radians.

Chord length = 5 units

Central angle = 2 radians

Calculate 'r' using the formula.

Find arc length as rθ.

3. Finding Arc Length Without the Central Angle:

The arc length can also be computed without knowing the central angle using the following methods:

4. Radius and Sector Area:

Substitute the values of the radius and sector area into the sector area formula.

Solve for the central angle.

Calculate the arc length using the relevant formula.

Example:

Calculate the arc length of a curve with a sector area of 25 square units and a radius of 2 units.

Sector area = 25 units

Radius = 2 units

Calculate the central angle using the formula.

Find arc length as radius × central angle.

5. Radius and Chord Length:

Substitute the values of the radius and chord length into the chord length formula.

Solve for the central angle.

Calculate the arc length using the relevant formula.

Example:

Calculate the arc length of a curve when its endpoints touch a chord of the circle, measuring 3 units. The radius of the circle is 2 units.

Chord length = 3 units

Radius = 2 units

Calculate the central angle using the formula.

Find arc length as radius × central angle.

These methods allow you to determine the arc length of a circle or curve under different conditions, whether you have information about the central angle, sector area, radius, or chord length.

Examples of Arc length

Example 1:

Find the length of an arc of a circle cut off by a central angle of 4 radians in a circle with a radius of 6 inches.

Solution:

Central angle, θ = 4 radians, radius, r = 6 inches. Use the arc length formula, L = θ × r = 4 × 6 = 24 inches.

Answer: Therefore, the arc length (PQ) is 24 inches.

Question 2:

The radius of the circle is 14 units, and the arc subtends 65 degrees at the center. What is the length of the arc using circumference?

Solution:

We know that,

Circumference of circle = 2πr

C = 2π × 14 = 28π

arc length = (θ/360) × C = (65°/360°)28π = 15.882 units

Answer: Arc length = 15.882 units.

Example 3:Calculate the length of an arc cut off by a central angle, θ = 40 degrees, in a circle with a radius of 4 inches.

Solution:

Radius, r = 4 inches, θ = 40 degrees. Use the arc length formula, L = π × (r) × (θ/180 degrees) = π × (4) × (40/180) = 2.79 inches.

Answer: Therefore, the length of the arc of the given circle is 2.79 inches.