
Mole Concept
Chemical Reaction And Equation of Class 10
MOLE CONCEPT
This topic includes the various basic concepts around which the whole of the chemistry revolves.
We can classify existing substances into following categories keeping mole concept in view.
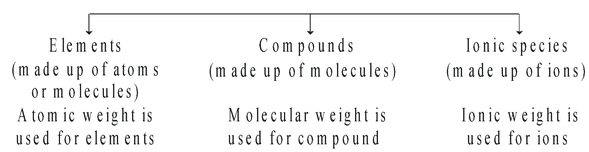
According to mole concept
Gram atomic weight (i.e. atomic weight in grams) of any element contains Avogadro number of atoms.
No. of gram atoms =
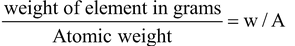
If w = A i.e. weight of an element in gram taken is equal to it’s atomic weight then number of gram atoms = 1 and we have already seen that when w = A then Avogadro no. of atoms are present so from here it is concluded that one gram atom of any element contains Avogadro number of atoms.
So, 56 g Fe = 1 g atom Fe = 6.023 x 10 23 Fe atoms.
Like wise 23 g Na = 1 g atom Na = 6.023 x 10 23 Na atoms
Examples
|
One mole of hydrogen atoms |
|
6.023 x 10 23 hydrogen atoms |
|
|
1 gm of hydrogen atoms |
|
|
One mole of carbon atoms |
|
6.023 x 10 23 carbon atoms |
|
|
12g of carbon |
|
|
One mole of NaCl |
|
6.023 x 10 23 Na + ions and 6.023 x 10 23 Cl - ions |
|
|
58.5 g of NaCl |
|
|
One mole of ammonia gas |
|
6.023 x 10 23 ammonia molecules |
|
|
17g of NH3 |
|
|
One mole of hydrogen |
|
6.023 x 10 23 hydrogen molecules |
|
|
2 g hydrogen |
A summary of different relationships in terms of Mole Concept.
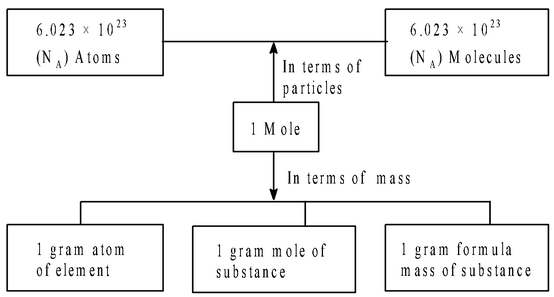
|
|
Moles of elements are referred as gram atoms and moles of ionic species is referred as gram ions. For ionic species no. of gram ions = weight of ion/ionic weight |
NOTE: 1 gram molecule or 32 grams or 1 mole of dry oxygen gas occupies 22.4 l at STP and contains 6.023 x 10 23 molecules of oxygen.
NOTE: 1 gram molecule or 4 gram or 1 mole of dry helium gas occupies 22.4 l at STP and contains 6.023 x 10 23 atoms because helium is a monoatomic gas .
For all solid and liquid substances, mole can be converted into weight or number of atoms or molecules. For gaseous substances, mole can also be converted into volume in addition to weight and number of particles.
Example
|
One mole of bromine liquid |
|
6.023 × 10 23 bromine molecules |
|
|
160 g of bromine |
|
|
One mole of chlorine gas |
|
6.023 × 10 23 chlorine molecules |
|
|
71 g of chlorine |
|
|
|
22.4 l chlorine at STP |
Illustration 1: Calculate the following for 49 g H 2 SO 4 .
a) Moles (b) Molecules (c) Total H atoms (d) Total S atoms
e) Total O atoms (f) Total electrons.
Solution : Molecular weight of H 2 SO 4 = 98
a) No. of moles = w/m = 49/98 = 1/2
b) Since 1 mole of any compound contains.
6.023 × 10 23 molecules.
So ½ mole will contain = ½ x 6.023 × 10 23 = 3 .0 x 10 23
c) 1 molecule of H 2 SO 4 contains 2H atoms
So total H atoms = 2 x 3 x 10 23 = 6 x 10 23
d) Total S atoms = 3. 0 x 10 23
e) Total O atoms = 3. 0 x 10 23 x 4 = 12 x 10 23
f) Electrons present in 1 molecule = 1 x 2 + 16 x 4 = 50
So Total electron present 50 x 3.0 x 10 23 = 150 x 10 23
Illustration 2 : Calculate total ions present in 4.2 g of N 3-
Solution : Weight of N 3- = 4.2 g
Ionic weight = 14
No. of gram ions = weight/ionic weight
= 4.2/14 = 0.3
Since one gram ion contains 6.023 × 10 23 ions.
So 0.3 gram ion will contains 0.3 x 6.023 × 10 23
= 1.8069 x 10 23 ions

CALCULATION OF MOLES OF A SUBSTANCE (ELEMENT or COMPOUND)
We have learnt that
1 Mole of an element = Gram atomic mass
1 Mole of a compound = Molar mass
Moles can be calculated from mass by using the relation
Moles of an element = Mass (in g)/Gram atomic mass(g/mol)
Moles of a compound = Mass (in g)/Molar mass (g/mol)
Or mass of the substance can be calculated as
Mass of an element (g) = Moles of element (mol) × (Gram atomic mass (g/mol)
Illustration 3 Convert into moles
(a) 90 g of water, (b) 12 g of oxygen, (c) 22 g of carbon dioxide.
Solution. We can calculate moles of substance by using this formula
Moles = Mass of substance/Molar mass
(a) Molar mass of H 2 O = 2 × 1 + 16 = 18 g mol –1
Moles of water = 90/18 = 5 mol
(b) Molar mass of oxygen = 2 × 16 = 32 g mol –1
Moles of oxygen = 12/32 = 0.375 mol
(c) Molar mass of CO 2 = 12 + 2 × 16 = 44
Moles of CO 2 = 22/44 = 0.5 mol
Related Topics
METHOD OF MOLES
This is an important method for solving stoichiometry problems
Steps for solving the problems
- Write balanced chemical equation of the reaction taking place between reactants.
- Check stoichiometric ratio and the ratio of amounts taken.
- If both ratio matches than any of the reactant with give the amount of products formed.
- If ratio doesn’t matches then find the limiting reactant. Now the amount of product formed will be governed by the limiting reactant.
Illustration 4: 0.5 moles of BaCl 2 is mixed with 0.2 moles of Na 3 PO 4 . Calculate maximum number of moles of Ba 3 (PO 4 ) 2 which can be formed.
Solution :
Step 1 : 3 BaCl 2 + 2Na 3 PO 4 → Ba 3 (PO4) 2 + 6NaCl
Step 2 : By viewing the balanced chemical equation we may well conclude that 3 moles of BaCl 2 react with two moles of Na 3 PO 4 and 1 mole of Ba 3 (PO 4 ) 2 is formed i.e. stoichiometric ratio among reactants is of 3 : 2 and we have taken 0.5 moles of BaC l2 and 0.2 moles of Na 3 PO4 i.e. ratio of amounts taken is of 5 : 2.
Step 3 : If these two ratio’s would have matched than any of the reactants will give the amount of product formed because if two ratio’s matches than both reactants are fully consumed.
Step 4 : Since ratio does not matches so one reactant is fully consumed (limiting reactant) and other is left (excess reactant).
Process for Finding Limiting Reactant
Assume any of the reactant to be limiting reactant. Our assumption may be right or wrong. Let BaCl2 is limiting
3BaCl 2 + 2Na3PO 4 → Ba 3 (PO 4 ) 2 + 6NaCl.
Initial Moles 0.5 0.2 0 0
Since BaCl 2 is assumed to be limiting so it is fully consumed i.e. 0.5 moles of BaCl 2 are consumed.
3 moles of BaCl 2 requires 2 moles of Na 3 PO 4 .
1 moles of BaCl 2 will require ⅔ moles of Na 3 PO 4 .
0.5 moles of BaCl 2 will require ⅓ moles of Na 3 PO 4 .
But we don’t have ⅓ moles of Na 3 PO 4 so our assumption that BaCl 2 is limiting is wrong. Now we will check for Na 3 PO 4 . Now we are assuming Na 3 PO 4 to be limiting i.e. 0.2 moles of Na 3 PO 4 are fully consumed.
Since 2 moles of Na 3 PO 4 requires 3 moles of BaCl 2 .
So 0.2 moles of Na 3 PO 4 will require 0.3 moles of BaCl 2 .
And we have 0.5 moles of BaCl 2 (far more than the requirement) so our assumption that Na 3 PO 4 is limiting is right.
3BaCl 2 + 2Na3PO 4 → Ba 3 (PO4) 2 + 6NaCl.
Initial Moles 0.5 0.2 0 0.
Since Na 3 PO 4 is limiting so it will govern the amount of products formed.
Moles after reaction 0.2 0 0.1
So moles of Ba 3 (PO 4 ) 2 formed = 0.1
|
|
Whenever two or more substances react their number of moles reacting might ormight not be same depending upon the stoichiometry of the reaction. |










