Linear Magnification Produced By Mirrors
Share
Linear Magnification Produced By Mirrors
Light of Class 10
LINEAR MAGNIFICATION PRODUCED BY MIRRORS
The linear magnification produced by a spherical mirror (concave or convex) is defined as the ratio of the height of the image (h′) to the height of the object (h). It is a pure ratio and has no units. It is denoted by the letter ‘m’ and is given by
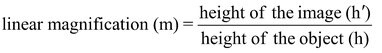
or m = h'/h
The linear magnification ‘m’ is also related to the object distance (u) and image distance (v). It can be expressed as :
Linear Magnification, m = -v/u
⇒ Linear magnification, m = h'/h = - v/u
This shows that the linear magnification produced by a mirror is also equal to the ratio of the image distance (v) to the object distance (u) with a minus sign.
IN CASE OF CONCAVE MIRROR:
(i) For real and inverted image: According to the New Cartesian Sign Convention, for the real and inverted images formed by a concave mirror,
object height (h) is always +ve.
image height (h′) is always –ve.
∴ Linear magnification, m = h'/h
m = -ve/+ve or m = -ve
(ii) For virtual and Erect image: According to the New Cartesian Sign Convention, for the virtual and erect images formed by a concave mirror,
object height (h) is always +ve.
image height (h′) is always +ve.
∴ Linear magnification, m = h'/h
m = +ve/+ve or m = +ve
- In case of a concave mirror, for the real and inverted images the magnification is always –ve. and for the virtual and erect images the magnification is always +ve.
IN CASE OF CONVEX MIRROR:
A convex mirror always forms a virtual and erect image.
For virtual and erect image : According to the New Cartesian Sign Convention, for the virtual and erect images formed by a convex mirror,
Object height (h) is always +ve.
Image height (h′) is always +ve.
∴ Linear magnification, m = h'/h
m = +ve/+ve or m = +ve
- In case of a convex mirror, which always forms virtual and erect image, the magnification is always +ve.
FOR SPHERICAL MIRRORS IF THE:
- Linear magnification, m > 1, the image is enlarged i.e. greater than the object
- Linear magnification, m = 1,the image is of the same size as the object.
- Linear magnification, m < 1.the image is diminished i.e. the image is smaller than the object.
Related Topics
