Distance Between Point and Line Formula
Euclidean geometry, determining the distance from a point to a line involves finding the shortest span between a specific point and any point along an infinitely extending straight line. This shortest distance is essentially the length of the line segment that connects the point to the nearest spot on the line, which is defined as the perpendicular distance from the point to the line. The formula for this distance can be expressed in various ways. Knowing how to calculate the distance from a point to a line is valuable in practical scenarios, such as measuring the separation between two objects like trees.
Also Check -
Volume of a Cylinder Formula
Understanding the Distance of a Point From a Line
The distance between a point and a line signifies the shortest possible gap between them, indicating the minimum distance needed to move from the point to a position on the line. This minimal length manifests as a line segment that is perpendicular to the line. Consider a Line L and a point X that does not fall on L:
Line and point
But how do we calculate the distance when the point isn't situated on the line? To address this, let's revisit the equation of a straight line and the distance formula. Additionally, think of a right-angled triangle ABC:
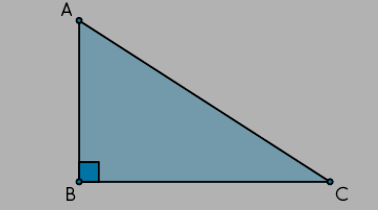
Right-angled triangle
Note that since ∠B = 90°, it's the largest angle in the triangle, implying that AC (the hypotenuse) is the longest side. This remains true in all cases. The hypotenuse AC will always surpass the perpendicular from A to BC, which is AB. Returning to our point and line, let's drop a perpendicular from X onto L:
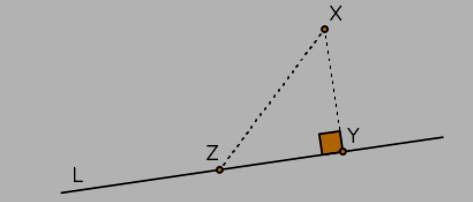
Shortest distance between point and line
In this diagram, Y represents the base of the perpendicular, while Z is any other point on L. It's important to realize that XY will always be shorter than XZ, regardless of where Z is positioned on the line. In simpler terms, the shortest distance from a point to a line follows the path of the perpendicular drawn from the point to the line. Consequently, we define the distance of a point X from a line L as the length of this perpendicular.
Also Check -
Volume of a Hemisphere Formula
Deriving the Formula for the Distance of a Point From a Line
Let's derive the formula to compute the distance of a point from a line by employing the distance formula and the triangle area formula.
Consider a line L in the XY-plane, with K(x₁, y₁) being a point at a distance 'd' from the line. The line L is represented by Ax + By + C = 0, where the x and y-intercepts are (-C/A) and (-C/B), respectively.
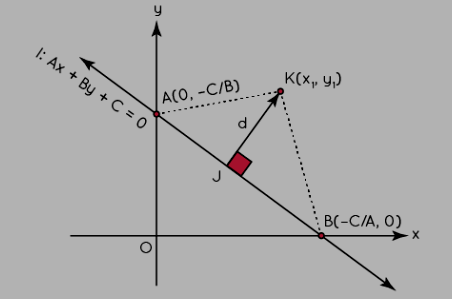
Distance of a point from a line
The line L intersects the x and y-axes at points B and A, respectively. KJ represents the perpendicular distance from point K, meeting the base AB of triangle KAB at point J. For the three given points K, B, and A, we have coordinates: K(x₁, y₁), B(x₂, y₂), and A(x₃, y₃).
Here, (x₂, y₂) = (-C/A, 0) and (x₃, y₃) = (0, -C/B).
We aim to find the perpendicular distance KJ = d.
The area of the triangle is calculated using the formula: Area (Δ KAB) = ½ base × perpendicular height
Area (Δ KAB) = ½ AB × KJ
⇒ KJ = 2 × area (Δ KAB) / AB -> (1)
In coordinate geometry, the area (Δ KAB) is computed as:
Area A = ½ |x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)|
= ½ |x₁(0 - (-C/B)) + (-C/A)((-C/B) - y₁) + 0(y₁ - 0
= ½ |(C/B) × x₁ - C/A ((-C/B) - y₁) + 0|
= ½ |(C/B) × x₁ - C/A ((-C-By₁)/B)|
= ½ |(C/B) × x₁ + C²/AB + ((BCy₁)/AB)|
= ½ |(C/B) × x₁ + (C/A) × y₁ + (C²/AB)|
= ½ |C(x₁/B + y₁/A + C/AB)|
By multiplying and dividing the expression by AB, we get:
= ½ |C(ABx₁/AB² + ABy₁/BA² + ABC²/AB²)|
= ½ |CA(x₁/AB + By₁/AB + C/AB)|
= ½ |C/(AB)| ⋅ |Ax₁ + By₁ + C| -> (2)
According to the distance formula, the distance of the line AB with coordinates A(x₁, y₁) and B(x₂, y₂) can be calculated as:
AB = √((x₂ - x₁)² + (y₂ - y₁)²)
Here, A(x₁, y₁) = A(0, -C/B), and B(x₂, y₂) = B(-C/A, 0).
AB = √(((-C/A)² - 0) + (0 - (-C/B)²))
= √((C²/A²) + (C²/B²))
Distance, AB = |C/AB| √(A² + B²) -> (3)
Substituting (2) and (3) into (1), we obtain:
The distance of the perpendicular KJ = d = |Ax₁ + By₁ + C| / √(A² + B²)
Therefore, the distance from a point (x₁, y₁) to the line Ax + By + C = 0 is given by |Ax₁ + By₁ + C| / √(A² + B²). It's important to enclose the numerator in absolute value signs since the distance must always be a positive value, and certain combinations of Ax₁, By₁, and C can yield negative results.
