
The Harmonic Mean Formula is indeed a valuable mathematical concept, especially when dealing with rates and inversely proportional quantities. It's one of the three Pythagorean means, with the other two being the arithmetic mean (AM) and the geometric mean (GM). Each of these means has its unique applications.
The arithmetic mean (AM) is the sum of a set of values divided by the number of values and is the most common type of average.
The geometric mean (GM) is used when dealing with exponential growth or values that are proportional to each other.
The harmonic mean formula, as you mentioned, is used when dealing with rates, speeds, or other inversely proportional data. It's defined as the reciprocal of the arithmetic mean of the reciprocals of a set of values. This makes it particularly useful in scenarios where you want to find the average rate or efficiency.
Understanding the relationships between these three means is essential in various fields like mathematics, statistics, physics, and engineering. They each have their unique strengths and applications, and knowing when to use which means is crucial for accurate analysis and calculations.
What is the Harmonic Mean Formula?
The harmonic mean formula is a type of average used in mathematics and statistics to calculate the average of a set of values, particularly when dealing with rates or inversely proportional quantities. It is defined as the reciprocal of the arithmetic mean of the reciprocals of a set of values. In mathematical terms, if you have a set of values x₁, x₂, x₃, ..., xₙ, the harmonic mean (HM) is calculated as:
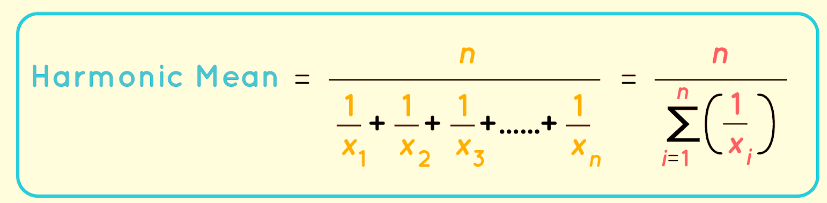
HM = n / [(1/x₁ + 1/x₂ + 1/x₃ + ... + 1/xₙ) / n]
The harmonic mean formula is especially useful when you want to find an average that reflects rates or speeds, as it gives more weight to smaller values in the dataset. It is one of the three Pythagorean means, along with the arithmetic mean and the geometric mean, each of which has its own specific use cases.
Harmonic Mean Formula Definition
The harmonic mean formula, often denoted as H or HM, is a type of mathematical average used to find the reciprocal of the arithmetic mean of the reciprocals of a set of values. In simpler terms, it is calculated as the number of values divided by the sum of the reciprocals of those values.
Harmonic Mean Formula Example
let's go through an example of how to calculate the harmonic mean:
Suppose we have a dataset of three values: 2, 4, and 8. We want to find the harmonic mean of these values.
First, calculate the reciprocals of the values:
Reciprocal of 2: 1/2
Reciprocal of 4: 1/4
Reciprocal of 8: 1/8
Next, sum these reciprocals:
(1/2) + (1/4) + (1/8) = 7/8
Now, divide the number of values (which is 3 in this case) by the sum of the reciprocals:
3 / (7/8) = 24/7
So, the harmonic mean of the values 2, 4, and 8 is 24/7.
Harmonic Mean Formula
If we have a set of observations given by x1, x2, x3....xn. The reciprocal terms of this data set will be 1/x1, 1/x2, 1/x3....1/xn. Thus, the harmonic mean formula is given by
- HM = n / [1/x1 + 1/x2 + 1/x3 + ... + 1/xn]
Here, the total number of observations is divided by the sum of reciprocals of all observations.
The formula is shown in sigma notation as well.
Harmonic Mean of Two Numbers
When calculating the harmonic mean of two numbers, a and b, the formula simplifies as follows:
HM = 2ab / (a + b)
This is a concise and handy way to find the harmonic mean of two non-zero values. It's a useful formula, especially in situations where you need to compute the harmonic mean quickly.
How to Find Harmonic Mean?
Your step-by-step process for finding the harmonic mean is accurate and follows the definition of the harmonic mean. Here's a summary of the steps:
- Take the reciprocal of each term in the data set.
- Count the total number of terms in the data set, which is n.
- Add all the reciprocal terms.
- Divide the value from step 2 by the value from step 3 to obtain the harmonic mean.
This is a clear and straightforward method to find the harmonic mean for any set of values. It's particularly useful when you want to calculate the harmonic mean manually or understand how it's derived.
Harmonic Mean Vs Geometric Mean
Harmonic mean and geometric mean are defined as the measures of central tendencies. Here are some of the differences enlisted between the two means:
| Harmonic mean | Geometric Mean |
| Given a data set, the harmonic mean can be evaluated by dividing the total number of terms by the sum of the reciprocal terms. | When we are given a data set consisting of n number of terms then we can find the geometric mean by multiplying all the terms and taking the n th root. |
| Its value is always lesser than the other two means. | Its value is always greater than the harmonic mean but lesser than the arithmetic mean. |
| It is the arithmetic mean of the data set with certain reciprocal transformations. | It can be thought of as the arithmetic mean with certain log transformations. |
| Example: If we are given a sequence 1, 2, 4, 7. n = 4 HM = 4 / (1/1 + 1/2 + 1/4 + 1/7) = 2.113 | Example: If we are given a sequence 1, 2, 4, 7. n = 4 GM = (1 × 2 × 4 × 7) 1/4 = 2.735 |
Harmonic Mean vs Arithmetic Mean
The differences between the harmonic mean and the arithmetic mean. While both are types of means, as you mentioned, they have distinct characteristics and use cases.
| Harmonic mean | Arithmetic Mean |
| To find this, we take the reciprocal of the arithmetic mean of the reciprocal terms in that data set. | To calculate this, we take the sum of all the observations in a data set and divide it by the total number of observations. |
| It is the lowest value amongst the three means. | It is the highest value among all three means. |
| It cannot be used on a data set consisting of negative or zero rates. | It can be calculated even if the data set has negative, positive, and zero values. |
| Example: 3, 2, 1, 6 n = 4 HM = 4 / (1/3 + 1/2 + 1/1 + 1/6) = 2 | Example: 3, 2, 1, 6 n = 4 AM = (3 + 2 + 1 + 6) / 4 = 3 |
Relation Between AM, GM, and HM
The relationships between the arithmetic mean (AM), geometric mean (GM), and harmonic mean (HM), as well as the conditions under which each of these means is typically used. To summarize:
AM = (a + b) / 2
HM = GM² / AM
HM ≤ GM ≤ AM
These formulas demonstrate the connections between these means and highlight their relative sizes. Your note about when to use each mean based on the nature of the data is also very useful. AM is indeed appropriate for data with the same units, GM for data with differing units, and HM for data expressed in rates or inversely proportional values.
This understanding can be incredibly valuable in various fields, such as statistics, finance, and engineering, for making meaningful calculations and comparisons.
Merits and Demerits of Harmonic Mean
Clear summary of the merits and demerits of the harmonic mean. It's essential to understand when and how to use this mean, as well as its limitations. Here's a concise breakdown of the points you mentioned:
Merits of Harmonic Mean:
- Based on observations, especially useful for averaging rates.
- Rigidly defined with a fixed value.
- Resistant to sample fluctuations.
- Requires all items of the series, which ensures a comprehensive calculation.
Demerits of Harmonic Mean:
- All elements of the series must be known; it cannot be calculated with missing data.
- Calculation method can be lengthy and complicated, especially for large datasets.
- If any term in the series is zero, the harmonic mean cannot be calculated.
- Extreme values in a series can greatly affect the harmonic mean, potentially making it less representative.
These points help to highlight both the strengths and weaknesses of the harmonic mean in various statistical and practical applications.
Uses of Harmonic Mean
some valuable real-life applications of the harmonic mean. Its unique properties make it a useful tool in various fields, particularly when dealing with ratios, averages, and multiplicative relationships. Here's a recap of the practical applications you mentioned:
- Patterns in the Fibonacci Series: The harmonic mean can help identify relationships and patterns within the Fibonacci series, which is a fascinating mathematical sequence found in nature and various scientific contexts.
- Finance: In finance, the Harmonic Mean Formula n can be employed when evaluating average multiples, such as price-earnings ratios or price-to-book ratios. It's particularly useful when dealing with financial data that involves ratios or inverse relationships.
- Speed Calculation: Speed is often expressed as a ratio of two different measuring units, like kilometers per hour (km/hr). The harmonic mean is suitable for calculating average speeds, taking into account the inverse proportionality between time and distance.
- Average of Rates: The Harmonic Mean Formula is ideal for calculating the average of rates, especially when dealing with various data points in a sample. It provides a fair way to average rates, assigning equal weight to each data point.
These practical applications showcase the versatility and relevance of the harmonic mean in different fields, from mathematics to finance and physics
Weighted Harmonic Mean
Weighted harmonic mean and its formula, which is indeed valuable when dealing with observations that have different weights. Here's a summary of the key points you've covered:
Weighted Harmonic Mean:
Used when different data points have varying weights.
The formula for the weighted harmonic mean, with normalized weights, is given as Σ(wi / xi) / Σwi, where wi are the weights and xi are the observations.
It can also be applied to frequency distributions by considering frequencies as weights.
Important Notes on Harmonic Mean
- Harmonic mean formula is used when you want to find the reciprocal of the average of the reciprocal terms in a series.
- The formula for harmonic mean is n / [1/x1 + 1/x2 + 1/x3 + ... + 1/xn].
- The relationship between harmonic mean (HM), geometric mean (GM), and arithmetic mean (AM) is GM² = HM × AM.
- In a dataset, HM will have the lowest value, GM will have the middle value, and AM will have the highest value.
These notes provide a solid foundation for understanding and applying the Harmonic Mean Formula , both in its standard form and when considering weights or frequency distributions.
| Related Links | |
| Fibonacci Sequence Formula | Eulers Formula |
| Exponential Formula | Factorial Formula |
Harmonic Mean Formula FAQs










