Perpendicular Lines
are a fundamental concept in geometry, representing a pair of lines that intersect each other at right angles, creating angles of 90 degrees at their point of intersection. These lines are all around us in our everyday environment, such as the corners of walls, the edges of a desk, and various architectural structures.
What is Perpendicular?
Perpendicular lines are indeed defined as lines that make a right angle with each other, creating angles of 90 degrees at their point of intersection. This concept is a fundamental part of geometry and has various practical applications.
Additionally, it's worth noting that perpendicular lines can also be defined as the shortest distance between a point and a line. This interpretation is particularly useful in problems involving point-to-line distances, as it allows for the calculation of the shortest distance between a specific point and a given line.
In your description, the lines AB and PQ intersecting at 90 degrees demonstrate a classic example of perpendicular lines. Furthermore, when you introduce the lines AB and CD as additional perpendicular lines, it reinforces the concept of multiple perpendicular relationships, which can be found in various geometric configurations and real-world scenarios.
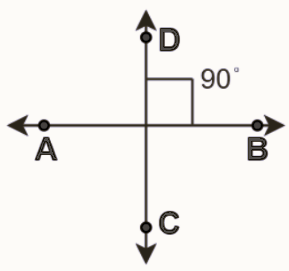
What is a Perpendicular Line?
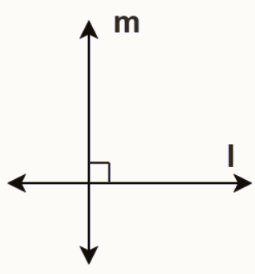
Perpendicular lines and the relationships between them. Perpendicular lines are defined by their intersection at a right angle of 90 degrees, as demonstrated by lines l and m meeting at point O in the figure you described. In this context, you can express this relationship as l ⊥ m, which signifies that line l is perpendicular to line m.
Any line parallel to line l is also perpendicular to line m. This is a fundamental property of perpendicular lines; they are always at right angles to any line parallel to them.
The concept of the shortest distance between a point and a line is closely related to the idea of perpendicular lines and can be particularly useful when dealing with geometry and practical applications where precise measurements are required.
Perpendicular Symbol
Perpendicular lines and the use of the symbol '⊥' to represent them is accurate. When two lines, such as lines l and m, intersect each other at a right angle (90 degrees), they are indeed called perpendicular lines and are represented as 'l ⊥ m.'
The point where these lines intersect, which is also referred to as the point of right-angle intersection, is known as the foot of the perpendicular. This point holds significance in geometry, especially when determining distances and constructing right angles. Your description effectively conveys these fundamental concepts related to perpendicular lines.
Properties of Perpendicular Lines
Perpendicular Lines:
Perpendicular lines are two lines that intersect at an angle of 90 degrees, forming a right angle at their point of intersection.
They have the unique property of always meeting at a right angle.
Parallel Lines:
When two lines are each perpendicular to the same line, they are always parallel to each other.
Parallel lines are lines that are equidistant from each other and do not intersect, maintaining the same separation throughout their length.
Understanding these properties is essential in geometry, mathematics, and various practical applications, where right angles and parallelism play crucial roles.
Also Check –
Factors and multiples Formula
Slope of Perpendicular Lines
The relationship between the slopes of perpendicular lines is accurate. When you have two lines, such as PQ and RS, that are perpendicular to each other, the product of their slopes is indeed equal to -1. This relationship can be expressed as:
m
1
.m
2
= -1
This property is a fundamental concept in geometry and is often used to identify perpendicular lines or to find the slope of one line when given the slope of a perpendicular line. Understanding the relationship between slopes is essential when working with perpendicular lines and their geometric properties.
Perpendicular Line Formula
Statement 1:
The product of the slopes of perpendicular lines is always -1.
Proof:
Consider the original line, which makes an angle θ with the X-axis.
A line perpendicular to the original will make an angle of θ + 90° or θ – 90° with the X-axis.
The slope of the original line is represented by tan θ.
The slope of the perpendicular line can be expressed as either tan (θ + 90°) or tan (θ – 90°).
Since tan (θ + 90°) = tan (θ – 90°) = -cot θ, the slope of the perpendicular line is -cot θ.
Now, when we multiply the slopes:
= tan θ × (-cot θ)
= -1
This demonstrates that the product of the slopes is always equal to -1.
Hence, the statement is proved.
Statement 2:
If the equation of a line is ax + by + c = 0, then the equation of a line perpendicular to the given line is -bx + ay + d = 0, where c and d are constants.
Proof:
Given the equation of the line: ax + by + c = 0
The slope of the line is -a / b.
Let the slope of the perpendicular line be denoted as m.
We know that the product of the slopes of two perpendicular lines is -1:
m × (-a / b) = -1
So, m = b / a.
Now, if the perpendicular line passes through a point (x1, y1), the equation of the perpendicular line is derived as follows:
(y - y
1
) / (x - x
1
) = b / a
ay - ay
1
= bx - bx
1
Rearranging terms, we have -bx + ay + (bx
1
- ay
1
) = 0.
Let's denote bx
1
- ay
1
as d. Thus, the required equation of the line is -bx + ay + d = 0.
This equation represents a line perpendicular to the original line and can be written in the form -bx + ay + d = 0, where c and d are constants.
Also Check –
Logarithm Formula
How to Draw Perpendicular Lines?
Constructing perpendicular lines using a protractor and a compass is a fundamental skill in geometry. Your step-by-step guide is clear and helpful for drawing a pair of perpendicular lines.
Drawing Perpendicular Lines using a Protractor:
Step 1:
Begin by drawing a horizontal line AB on a piece of paper using a ruler.
Step 2:
Choose any point P on line AB from which you want to draw the perpendicular line.
Step 3:
Place the protractor on the line in such a way that the midpoint of the protractor aligns with point P on the line.
Step 4:
Use the protractor to mark a 90-degree angle.
Step 5:
Using a ruler, draw a line at a 90-degree angle from point P. This new line will be perpendicular to the original line AB, creating a pair of perpendicular lines.
This method allows you to construct perpendicular lines accurately and is a valuable skill for various geometric and architectural applications.
Perpendicular Lines Real-Life Examples
Perpendicular lines, as you correctly mentioned, are lines that intersect each other at right angles, forming angles of 90 degrees. They are indeed prevalent in our daily lives and are often observed in various real-life situations, such as:
Corners of Rooms:
In architecture and interior design, the corners of rooms are intentionally constructed to be perpendicular to each other, ensuring structural stability and right angles in the layout of buildings.
Clock Hands at 3 o'clock:
At 3 o'clock on a clock face, the hour and minute hands are perpendicular to each other, illustrating the concept of perpendicular lines. This is one of the ways we tell time.
Corners of Tables and Desks:
The corners of tables, desks, and various furniture pieces are often designed to be perpendicular, not only for functional stability but also for aesthetic reasons.
Recognizing perpendicular lines in these everyday examples demonstrates their significance in architecture, timekeeping, and design, where right angles and structural integrity are crucial.
Also Check –
Rational Number Formula
Perpendicular Lines Examples
Example 1: Given the line equation 2x - 3y + 6 = 0. Determine the equation of a line perpendicular to this line and passing through the point (4, 5).
Solution:
Find the slope of the given line:
The slope of 2x - 3y + 6 = 0 is -2/3.
Use the condition for perpendicular lines:
The slope of the perpendicular line will be 3/2 (the negative reciprocal of -2/3).
Use the point-slope form to find the equation of the perpendicular line:
(y - 5) = (3/2)(x - 4).
Example 2: Determine whether the lines 5x - 2y + 3 = 0 and 2x + 5y - 7 = 0 are perpendicular to each other.
Solution:
Find the slopes of both lines:
The slope of 5x - 2y + 3 = 0 is 5/2, and the slope of 2x + 5y - 7 = 0 is -2/5.
Check if the product of the slopes is -1:
(5/2) * (-2/5) = -1. Since the product of the slopes is -1, the lines are indeed perpendicular.
Example 3: Find the equation of the line that is perpendicular to the line 3x + 4y - 12 = 0 and passes through the point (2, -1).
Solution:
Calculate the slope of the given line:
The slope of 3x + 4y - 12 = 0 is -3/4.
Determine the slope of the perpendicular line:
The slope of the perpendicular line will be 4/3 (the negative reciprocal of -3/4).
Use the point-slope form to find the equation of the perpendicular line:
(y + 1) = (4/3)(x - 2).
These examples demonstrate how to work with perpendicular lines and how to find equations of lines that are perpendicular to a given line while passing through specific points.
