
Product Rule Formula: The product rule in calculus is a technique used to find the derivative of a function that is expressed as the product of two differentiable functions. In other words, when you have a function in the form of f(x)·g(x), where both f(x) and g(x) are differentiable, you can apply the product rule, also known as the Leibniz rule, to determine its derivative. The product rule is derived directly from the fundamental concepts of limits and derivatives in calculus. In the sections, we will deal with the details of the product rule formula, provide a proof of its validity, and offer solved examples to illustrate its application.
What is the Product Rule?
The product rule in calculus is a technique used to find the derivative of a function of two differentiable functions. In simple terms, it states that the derivative of the product of two differentiable functions is equal to the sum of two products: the second function times the derivative of the first function, plus the first function times the derivative of the second function. Mathematically, if you have a function in the form of f(x)·g(x), you can find its derivative using the product rule as follows:
d/dx [f(x)·g(x)] = g(x) × f'(x) + f(x) × g'(x)
This formula provides a method to efficiently calculate the derivative of a product of two functions, which is a common occurrence in calculus and mathematical modeling.
Product Rule Formula
Product Rule Formula is essential for finding the derivative of a product of two differentiable functions. It allows you to determine the rate of change of the product of these functions. Here's a breakdown of the formula:
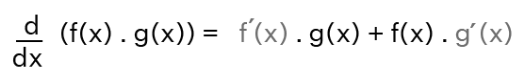
If you have a function f(x), which is the product of two differentiable functions u(x) and v(x), you can calculate its derivative as:
d/dx [f(x)] = d/dx [u(x)·v(x)] = v(x) × u'(x) + u(x) × v'(x)
In this formula:
f(x) represents the product of the differentiable functions u(x) and v(x).
u(x) and v(x) are the individual differentiable functions.
u'(x) is the derivative of the function u(x).
v'(x) is the derivative of the function v(x).
By applying the product rule, you can efficiently find the derivative of a product of functions, making it a valuable tool in calculus and mathematical analysis.
Derivation of Product Rule Formula
The product rule in calculus is a fundamental concept for finding the derivative of a product of two differentiable functions. The product rule formula is often given as:
(u v)' = u' · v + u · v'
or in Leibniz's notation:
d/dx (u · v) = (du/dx) · v + u · (dv/dx)
can be proved using different methods. Two common methods for proving the product rule formula are as follows:
Using the First Principles: This method involves using the definition of the derivative based on the limit definition. It starts with the definition of the derivative and proceeds to derive the product rule. This proof is typically more rigorous and may involve limit calculations.
Using the Chain Rule: The chain rule is another fundamental rule in calculus that relates the derivative of a composite function to the derivatives of its individual components. By applying the chain rule to the product of two functions, you can derive the product rule. This method is often more straightforward and commonly used in introductory calculus courses.
Both methods lead to the same result, the product rule formula, and are valid ways to prove and understand how to calculate the derivative of a product of functions. The choice of method may depend on the level of mathematical rigor and the specific context in which you are working.
Product Rule Formula Proof Using First Principle
To prove product rule formula using the definition of derivative or limits, let the function h(x) = f(x)·g(x), such that f(x) and g(x) are differentiable at x.
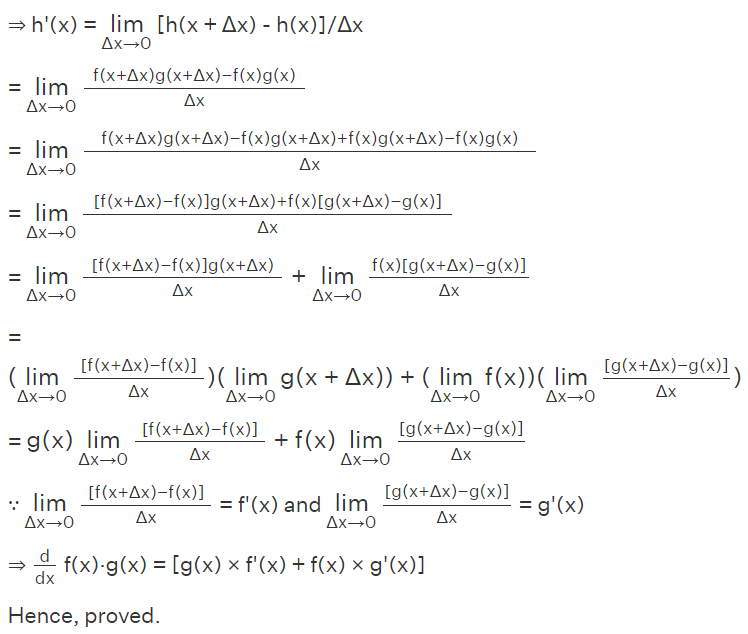
Product Rule Formula Proof Using Chain Rule
The product rule in calculus can be derived by treating it as a specific application of the chain rule. Let's consider a differentiable function f(x) such that h(x) = f(x)·g(x).
By applying the chain rule, we can express the derivative of the product f(x)·g(x) as the sum of two terms: one involving the derivative of f with respect to x and the other involving the derivative of g with respect to x.
In mathematical terms:
d/dx (f·g) = [∂(fg)/∂f] * [df/dx] + [∂(fg)/∂g] * [dg/dx]
Simplifying this expression, we arrive at the familiar product rule formula:
d/dx (f·g) = g * (df/dx) + f * (dg/dx)
Therefore, we have successfully proved the product rule using the chain rule as a foundational concept in calculus.
Product Rule of More Than Two Functions
The product rule can be generalized to products of more than two factors using the same product rule formula. For example, for three functions, u(x), v(x), and w(x), product given as u(x)v(x)w(x), we have,
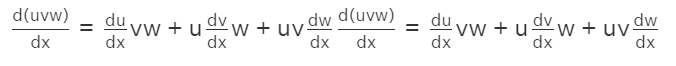
How to Apply Product Rule in Differentiation?
The steps you've outlined for finding the derivative of a function h(x) = f(x)·g(x) using the product rule are accurate and well-structured. The product rule is an important tool in calculus that is used for calculating the derivative of a product of two differentiable functions. Here's a summary of the steps, followed by an example to illustrate the process:
Step 1: Identify the functions f(x) and g(x) involved in the expression.
Step 2: Find the derivatives of f(x) and g(x) separately, denoted as f'(x) and g'(x), respectively.
Step 3: Apply the product rule formula to determine the derivative of the product function h(x):
h'(x) = d/dx [f(x)·g(x)] = [g(x) × f'(x) + f(x) × g'(x)]
Let's examine an example to better understand how to use the product rule:
Example: Find the derivative of the function f(x) = x·log(x).
Solution:
Here, f(x) = x·log(x).
Identify u(x) = x and v(x) = log(x).
Calculate the derivatives: u'(x) = 1 and v'(x) = 1/x.
Apply the product rule formula:
f'(x) = [v(x)u'(x) + u(x)v'(x)]
f'(x) = [log(x)·1 + x·(1/x)]
f'(x) = log(x) + 1
Answer: The derivative of the function x·log(x) using the product rule is log(x) + 1.
This example demonstrates the application of the product rule
Product Rule Formula Application
The product rule formula is a fundamental concept in calculus and is widely applied in various scenarios where functions are expressed as products of other functions. Here are some common applications of the product rule formula:
- Physics: In physics, the product rule is used to find the derivative of equations that describe the behavior of physical systems. For example, when determining the velocity of a particle in motion or the rate of change of momentum, the product rule is applied to functions involving time and distance or mass and velocity.
- Economics: Economists use the product rule to analyze economic models that involve the interaction of multiple variables. When studying production functions, cost functions, or utility functions, the product rule helps in finding the rate of change with respect to different parameters.
- Engineering: Engineers frequently use the product rule in fields such as mechanical engineering, civil engineering, etc. It helps when calculating the rates of change in complex systems involving variables like voltage, current, force, or stress.
- Biology: Biologists apply the product rule in the study of population growth models, genetics, and the diffusion of substances through membranes. For instance, when modeling population growth, the product rule helps determine how the population size changes over time due to birth and death rates.
- Finance: In finance, the product rule can be employed when analyzing the pricing of financial derivatives, interest rate models, and options. It assists in calculating the sensitivity of option prices to changes in underlying asset values.
| Related Links | |
| Product to Sum Formula | Profit Margin Formula |
| Pyramid Formula | Pythagorean Triples Formula |
Product Rule Formula FAQs
Q1. Define the product rule in calculus.
Q2. When should I use the product rule?
Q3. What is the formula for the product rule?
Q4. Can the product rule be applied to more than two functions?










