
Rectangular Parallelepiped Formula: A parallelepiped is a geometric solid made up of six parallelograms. Its name, "parallelepiped," originates from the Greek word "parallelepipedon," signifying "a figure with parallel sides." Much like a cube's connection to a square, a parallelepiped is related with a parallelogram. It comprises six faces in the shape of parallelograms, eight vertices, and twelve edges. The subsequent sections will explore its properties and various formulas concerning the calculation of its surface area and volume.
What is Rectangular Parallelepiped Formula
It's a three-dimensional geometric shape characterized by six faces, all of which take the shape of a parallelogram. With its 6 faces, 8 vertices, and 12 edges, it's a foundational form encompassing specific cases like the cube, cuboid, and rhomboid. A cube is a type of parallelepiped featuring all sides in a square shape. Similarly, a cuboid and a rhomboid are parallelepipeds with faces in the shape of a rectangle and a rhombus, respectively. In the diagram below, observe a parallelepiped, with 'a', 'b', and 'c' representing side lengths, and 'h' as the height of this geometric figure.
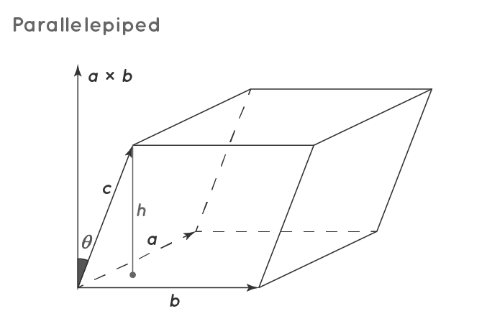
Rectangular Parallelepiped Formula Properties
Distinctive traits differentiate a parallelepiped from other 3-D shapes. These characteristics include:
- A parallelepiped is a three-dimensional solid shape.
- It comprises 6 faces, 12 edges, and 8 vertices.
- All faces within a parallelepiped take the shape of a parallelogram.
- Each face possesses 2 diagonals known as face diagonals, totaling 12 face diagonals.
- The diagonals connecting non-co-planar vertices are termed body or space diagonals within a parallelepiped.
- It can be described as a prism with a base in the shape of a parallelogram.
- Each face of the parallelepiped serves as the mirror image of its opposite face.
Rectangular Parallelepiped Formula Surface Area
The surface area of a parallelepiped represents the collective area enclosed by all its surfaces. This measurement is typically expressed in square units, such as in2, cm2, m2, ft2, yd2, etc. The surface area of a parallelepiped comprises two types:
- Lateral Surface Area
- Total Surface Area
Rectangular Parallelepiped Formula Lateral Surface Area
The lateral surface area of a parallelepiped refers to the collective area of its side or lateral faces. To compute the LSA of a parallelepiped, the total area covered by the four side faces needs to be summed.
Rectangular Parallelepiped Formula Total Surface Area
The total surface area of a parallelepiped encompasses the combined area of all its faces. To determine the TSA (Total Surface Area) of a parallelepiped, the sum of the area covered by its six faces needs to be calculated.
Rectangular Parallelepiped Formula Surface Area
The formulas for determining the lateral surface area (LSA) and total surface area (TSA) of a parallelepiped are expressed as follows:
LSA of Parallelepiped = P × H
TSA of Parallelepiped = LSA + 2 × B = (P × H) + (2 × B)
Here,
B = Base area
H = Height of the parallelepiped
P = Perimeter of the base shape
Rectangular Parallelepiped Formula Volume
The volume of a parallelepiped represents the space it occupies in a three-dimensional plane. This measurement is typically expressed in cubic units, such as in3, cm3, m3, ft3, yd3, etc.
Formula for Parallelepiped Volume
The formula to compute the volume of a parallelepiped involves the base area and the height. It is represented as:
V = B × H
Where,
B = Base area
H = Height of the parallelepiped
The parallelepiped is a three-dimensional shape composed of six faces, all in the form of parallelograms. It possesses specific properties setting it apart from other 3D figures, such as having 6 faces, 8 vertices, and 12 edges. The surface area of a parallelepiped includes both the lateral surface area (LSA) and the total surface area (TSA), calculated based on the faces and perimeter of the base.
Additionally, its volume, calculated by multiplying the base area and height, determines the space it occupies in a three-dimensional space. Understanding these fundamental properties, surface area, and volume formulas contributes to a comprehensive grasp of the parallelepiped's geometric characteristics.
Explore Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your Maths knowledge. and build a strong foundation.
| Related Links | |
| Population Mean Formula | Polygon Formula |
| Natural Log Formula | Normal Distribution Formula |
Rectangular Parallelepiped Formula FAQs
What is a rectangular parallelepiped?
How many edges, vertices, and faces does a rectangular parallelepiped have?
What is the formula for the volume of a rectangular parallelepiped?
What is the formula for the total surface area of a rectangular parallelepiped?
How is the lateral surface area of a rectangular parallelepiped calculated?










