
Root Mean Square Speed of Gas Molecules: A small fraction of molecules exhibit either extremely high or extremely low speeds. Most molecules are near the RMS speed at the midpoint of the range of molecular speeds. The entirety of the area under the curve in the figure represents the total count of molecules in the collection.
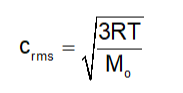
It is represented by Root Mean Square Speed of Gas Molecules Crms = root square mean value
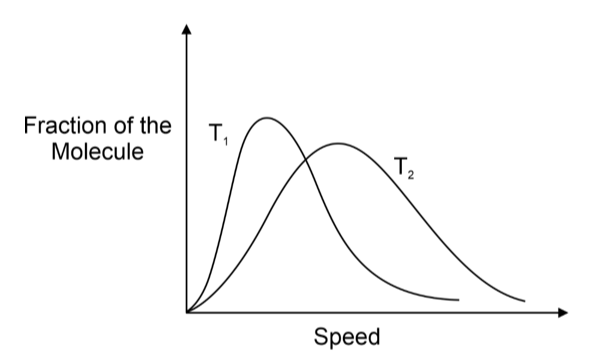
As temperature increases, the kinetic energy of gas molecules rises, causing a decrease in the proportion of molecules with lower speeds and an increase in the fraction with higher speeds. At higher temperatures, the curve shifts to higher values, yet the respective proportions of molecules decrease. Consequently, the speed distribution is broader at higher temperatures compared to lower temperatures, as depicted in the figure (T2 > T1).
Root Mean Square Speed of Gas Molecules
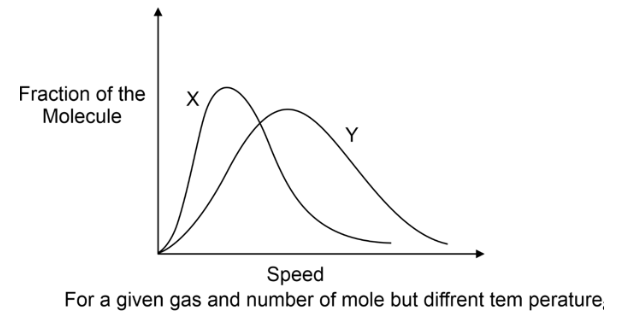
The distribution of molecular speeds is influenced by the mass of the gas molecule. At an equivalent temperature, a heavier gas molecule displays a narrower spread of speeds compared to a lighter gas molecule, as illustrated in the subsequent diagram (MX > MY).
According to the kinetic theory of gases, every molecule moves at a different velocity. In a given mass of gas, let 'n' represent the total number of molecules, where 'n1' molecules move at a speed of 'v1', 'n2' molecules at 'v2', and so on, up to 'nn' molecules at a speed of 'vn'.
Root mean Square (Crms) speed formulas
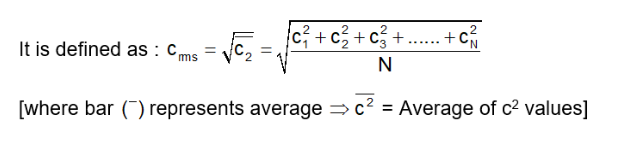
Since the distribution is continuous, we can express:
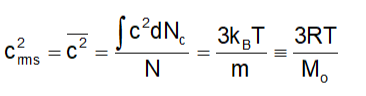
Where Mo = Mol. Mass of the gas (in kg)
Derivations of Root Mean Square Speed of Gas Molecules
Visualise a cube with an edge-length of 'l', holding 'N' molecules, each with a mass 'm'. These molecules move randomly in all directions, encompassing a broad spectrum of speeds. The velocity 'u1' of any molecule can be decomposed into three component velocities denoted as 'ux', 'uy', and 'uz'. These velocities span the three directions perpendicular to one another and aligned with the sides of the cube, as illustrated in the figure. The relationships between these component velocities are expressed by the following equation:
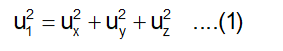
When considering the x-component motion of a molecule, the momentum of the molecule before colliding with the side ABCD will be equal to mux.
Momentum of the molecule after collision with the side ABCD = –mux.
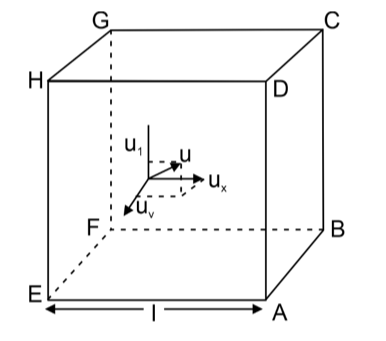
The change in momentum of the molecule during a single collision with the side ABCD is |2mux|. Considering 'l' as the edge length of the cube, the molecule travels a distance of 2l to return to the wall ABCD. The frequency of collisions per unit of time with the wall ABCD is equivalent to ux/2l.
Hence, the overall change in momentum per unit time due to these collisions is:
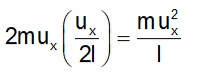
According to Newton’s second law of motion
Force = mass × acceleration
mass x d(velocity)/dt
= d/dt (mass x velolcity)
= d/dt(momentum = rate of change of momentum
Therefore, the overall force resulting from the impacts of a solitary molecule with the wall ABCD of the container is Mux2/l. The area of the wall is l^2. Consequently, the pressure exerted due to the collisions involving the x-component velocity of an individual molecule with the side ABCD is:
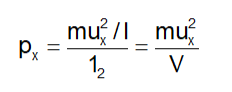
where V is the volume of the vessel
Since each molecule exerts an equal amount of pressure, the total pressure exerted on the wall ABCD will be:
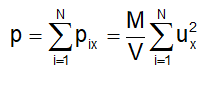
Defining the mean square speed as

Since the directions x, y and z are equivalent, we will also have
But from Eq. (1), we will have
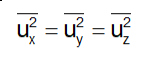
From Eqs (1) and (3), we can write
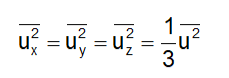
Substituting this in Eq. (2), we get
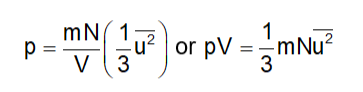
From Maxwell distribution, we already know
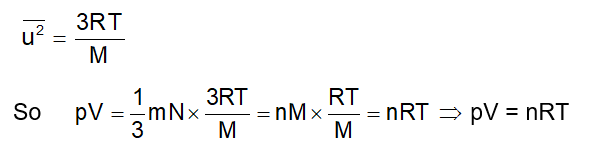
Average translational kinetic = ½ murms2 = 3/2kT energy per molecule
Average Translational Kinetic = NA × ½ murms2 = 3/2RT energy per mole
k(Boltzmann constant) = R/NA = 1.38 × 10–23 JK–1
| Related Links | |
| Potassium Chlorate Formula | Potassium Bromate Formula |
| Gold Formula | Phosphate Formula |
Root Mean Square Speed of Gas MoleculesFAQs
What is the root mean square (RMS) speed of gas molecules?
What factors influence the RMS speed of gas molecules?
Why is the RMS speed important in understanding gas behaviour?










