Secant Square x Formula, Derivation, Solved Examples
Manoj Kumar3 Nov, 2023
Share
Secant Square x Formula: Trigonometric functions describe the relationship between angles and sides. There are six main trigonometric functions: sine, cosine, tangent, cotangent, cosecant, and secant. These functions provide various values for different angles such as 30°, 60°, and more. Among these functions, sine, cosine, and tangent are the fundamental ones for classifying trigonometric functions.
Secant Square x Formula(sec 2 x):
sec 2 x=1+tan 2 x
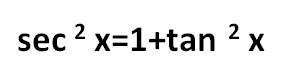
Derivation of the Secant Square x Formula
In trigonometry, the functions sec θ and tan θ represent the secant and tangent functions, respectively. According to the Pythagorean identity for these functions, they can be expressed as: Sec 2 θ−Tan 2 θ=1 This equation can be rearranged to solve for Secant squared:Sec 2 θ=1+Tan 2 θ
This derivation confirms that the secant squared x formula equals the sum of one and the tangent squared x function. Another approach to derive the Secant Square x Formula involves the identity related to the sum of squares of sine and cosine ratios: We start with the identity:sin 2 x+cos 2 x=1
Dividing both sides by cos 2 x:( sin 2 x/cos 2 x )+( cos 2 x/ cos 2 x )= 1 / cos 2 x
This simplifies to: tan 2 x+1=sec 2 x Hence, it leads to the conclusion that the Secant Square x Formula issec 2 x=1+tan 2 x.
Secant Square x Formula Solved Examples
Example 1: Given: tanx= 3/5
Solution: Secant Square x Formula Sec 2 x=1+tan 2 x = 1 + ( 3/ 5 ) 2 =1+( 3/5 ) 2 = 1 + 9 /25 =1+ 9/25 = (25 + 9) /25 = 34 /25 Therefore, Sec 2 x= 34 /25Example 2: Given: tanx= 4/5
Solution: Secant Square x Formula Sec 2 x=1+tan 2 x = 1 + ( 4 /5 ) 2 =1+( 4/5 ) 2 = 1 + 16 /25 =1+ 16 / 25 = 41 /25 Therefore, Sec 2 x= 41 /25Example 3: Simplify (1+tan 2 A)(1−sinA)(1+sinA)
Solution: (1+tan 2 A)(1−sinA)(1+sinA) =(1+tan 2 A)(1−sin 2 A) = sec 2 A⋅cos 2 A =( 1/ cos 2 A )⋅cos 2 A = 1Example 4: Determine the value of sec 2 x when tanx= 2/5 .
Solution: Given tanx= 2/5 . Using the Secant Square x Formula: sec 2 x=1+tan 2 x = 1 + ( 2/ 5 ) 2 =1+( 2/5 ) 2 = 1 + 4 /25 = = (25 + 4) / 25 = 29/ 25 Hence, sec 2 x equals 29/25 when tanx is given as 2/5 .Example 5: Find the value of sec 2 x if cotx= 2/5 .
Solution: Given that cotx= 2/5 . Thus, tanx= 1/ cotx = 5/2 . Now, applying the Secant Square x Formula: sec 2 x=1+tan 2 x = 1 + ( 5/2 ) 2 =1+( 5/2 ) 2 = 1 + 25/4 = 29 /4 = 29/4 Therefore, when cotx= 2/5 , the value of sec 2 x is 29/ 4 .Example 6: Determine the value of sec 2 x when tanx= 1/5 .
Solution: Given tanx= 1/5 . Using the Secant Square x Formula: sec 2 x=1+tan 2 x = 1 + ( 1/ 5 ) 2 =1+( 1/5 ) 2 = 1 + 1 /25 = = (25 + 1) / 25 = 26/ 25 Hence, sec 2 x equals 26/25 when tan tanx is given as 1/5 .Solved examples demonstrate the practical application of this formula to find secant squared values for given tangent of cotangent ratios. Mastering this formula allows for quick calculations and deeper comprehension of trigonometric relationships in various problem-solving scenarios.
Secant Square x Formula and its derivations is pivotal in trigonometry, offering insights into the relationship between secant and tangent functions. The formula sec2x = 1 + tan2x is derived through Pythagorean identities and relationships among sine, cosine, secant, and tangent functions.
Explore Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your Maths knowledge. and build a strong foundation.
| Related Links | |
| Surface Area of a Prism Formula | T-Test Formula |
| Trajectory Formula | U Substitution Formula |
Secant Square x Formula FAQs
What is the Secant Square x Formula?
How is the Secant Square x Formula derived?
Why is the Secant Square x Formula significant?
How can the Secant Square x Formula be applied in problem-solving?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
