
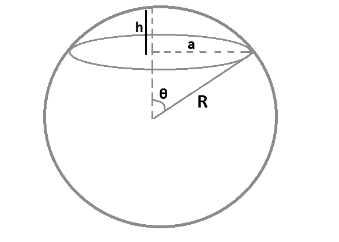
Spherical Cap Volume Formula: A spherical cap is a geometric shape derived from a sphere through a plane cut. It represents the portion of the sphere that protrudes beyond the intersecting plane. This cap is formed when a portion of the sphere is removed by a cutting plane. To determine the volume of a spherical cap, one needs to know its base area, height, and the radius of the original sphere.
The formula to calculate the volume of a spherical cap is given by:
Spherical Cap Volume Formula V= 1/3 π(3R−h)h 2
Where: R represents the sphere's radius, h is the height of the spherical cap, π is a constant equal to 22/ 7 .
By utilizing the Pythagorean theorem, we can express
(R−h) 2 +a 2 =R 2 . Hence, the formula can also be expressed as:
Spherical Cap Volume Formula V= 1/6 πh(3a 2 +h 2 ) Here, the symbol a denotes the radius of the spherical cap.
Spherical Cap Volume Formula Solved Examples
Example 1: Given the radius of the sphere as 7 m and the height of the cap as 10 m.
Using the Spherical Cap Volume Formula: 1/3 π(3R−h)h 2
Given values: R=7 and h=10
Substituting the values: 1/3 × 22/7 ×(3×7−10)×10 2
V= 1/3 × 22/7 ×11×100
V=1152 cubic metres
Example 2: Given the radius of the sphere as 5 m and the height of the cap as 5 m.
Using the Spherical Cap Volume Formula: V= 1/3 π(3R−h)h 2
Given values: R=5 and h=5
Substituting the values: 1/3 × 22/7 ×(3×5−5)×5 2
V= 1/3 × 22/7 ×10×25
V=261.9cubic meters
Example 3: Given the radius of the sphere as 7.5 m and the height of the cap as 12 m.
Using the Spherical Cap Volume Formula V= 1/3 π(3R−h)h 2
Given values: R=7.5 and h=12
Substituting the values:
V= 1/3 × 22/7 ×(3×7.5−12)×12 2
V= 1/3 × 22/7 ×17.5×144
V=1583.5cubic metres
Example 4: Given the height and volume of a spherical cap are 8 meters and 603.2 cubic meters, respectively. Find the radius of the sphere.
Solution: Given: h=8 and V=603.2
Using the Spherical Cap Volume Formula: V= 1/3 π(3R−h)h 2
Substituting the known values: 603.2= 1/3 ×π×(3R−8)×8 2
603.2 = 1/3 ×π×(192R−512)
1809.6 =π×(192R−512)
1809.6/π = (192R−512)
192R = 1809.6/π + 512
R = (1809.6/π + 512)/192
Example 5: Determine the volume of a spherical cap with a sphere radius of 12 m and a cap height of 5 m.
Solution: Given: R=12 and h=5
Using the Spherical Cap Volume Formula: V= 1/3 π(3R−h)h 2
Substituting the known values:
V= 1/3 ×π×(3×12−5)×5 2
V= 1/3 ×π×31×25
V= 775π/3
T hese problems illustrate how to find the radius of a sphere or the volume of a spherical cap using the provided height, radius, and volume information along with the formulas associated with spherical caps.
A spherical cap is a section obtained by slicing a sphere with a plane. The formula to calculate its volume involves the radius of the sphere ( R) and the height of the cap (h). Through different examples, the process of finding the volume of a spherical cap or determining the sphere's radius using the given cap's volume and height is demonstrated.
These calculations rely on established formulas for the volume of a spherical cap and involve substituting the known values to arrive at the final volume in cubic units or to solve for the sphere's radius. Understanding these formulas and examples enables the determination of key geometric measurements related to spherical caps, providing a practical approach to solve for unknown values using given parameters.
| Related Links | |
| Hexagonal Pyramid Formula | Hypothesis Testing Formula |
| Interquartile Range Formula | Inverse Variation Formula |
Spherical Cap Volume Formula FAQs
What is a spherical cap?
What is the formula for calculating the volume of a spherical cap?
Can the volume of a spherical cap be calculated with a different formula?
What does the formula for the spherical cap volume involve?
How is the spherical cap volume formula applied in real-world problems?










