

CBSE Class 12 Maths Notes Chapter 11: CBSE Class 12 Maths Notes Chapter 11 Three Dimensional Geometry, covers the study of lines, planes, and their interactions in 3D space. It introduces the Cartesian coordinate system in three dimensions, direction cosines and direction ratios of a line, and equations of a line in different forms.
CBSE Class 12 Maths Notes Chapter 11 also explores the angle between two lines, the shortest distance between skew lines, and equations of a plane. Additionally, it focuses on finding the angle between two planes, the angle between a line and a plane, and the distance between a point and a plane. These concepts are essential for understanding spatial relationships.CBSE Class 12 Maths Notes Chapter 11 Overview
CBSE Class 12 Maths Notes Chapter 11 PDF
Below we have provided CBSE Class 12 Maths Notes Chapter 11 Three Dimensional Geometry pdf for the ease of the students so that they can download the CBSE Class 12 Maths Notes Chapter 11 Three Dimensional Geometry pdf and access it without internet.CBSE Class 12 Maths Notes Chapter 11 PDf
CBSE Class 12 Maths Notes Chapter 11 Three Dimensional Geometry
Below is the CBSE Class 12 Maths Notes Chapter 11 Three Dimensional Geometry -Direction Cosines of a Line
The direction cosines of a line are cos, cos, and cos if the directed line OP makes angles, and with positive X, Y, and Z axes, respectively. The letters l, m, and n stand for them. Consequently, cos γ = l, cos β = m, and cos γ = n. In addition, the total of a line's direction cosines squares is always 1. i.e. l 2 + m 2 + n 2 = 1 or cos 2 α + cos 2 β + cos 2 γ = 1 Note: Direction cosines of a directed line are unique.Direction Ratios of a Line
Number proportional to the direction cosines of a line, are called direction ratios of a line.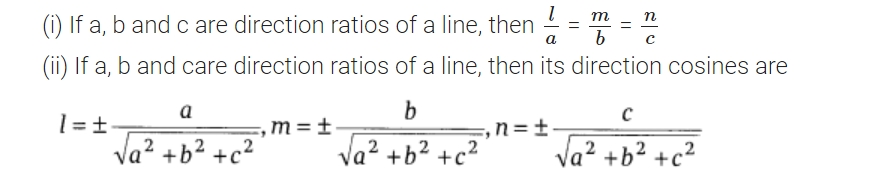 (iii) Direction ratios of a line PQ passing through the points P(x
1
, y
1
, z
1
) and Q(x
2
, y
2
, z
2
) are x
2
– x
1
, y
2
– y
1
and z
2
– z
1
and direction cosines are
(iii) Direction ratios of a line PQ passing through the points P(x
1
, y
1
, z
1
) and Q(x
2
, y
2
, z
2
) are x
2
– x
1
, y
2
– y
1
and z
2
– z
1
and direction cosines are
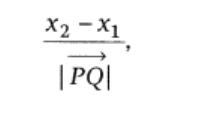
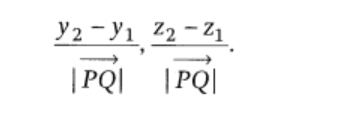 It should be noted that
(i) the direction ratios of two parallel lines are equal.
(ii) A line's direction ratios are not unique.
It should be noted that
(i) the direction ratios of two parallel lines are equal.
(ii) A line's direction ratios are not unique.
Straight line: A straight line is a curve, such that all the points on the line segment joining any two points of it lies on it.
 where a, b, and c are the line's direction ratios and (x1, y1, z1) is the place the line is passing through.
If the line's direction cosines are l, m, and n, then the line's equation is
where a, b, and c are the line's direction ratios and (x1, y1, z1) is the place the line is passing through.
If the line's direction cosines are l, m, and n, then the line's equation is
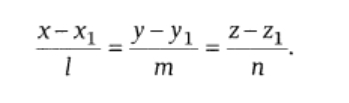 Point to remember: We must first confirm that the coefficients of x, y, and z are unity with a positive sign before using the DRs of a line.
Point to remember: We must first confirm that the coefficients of x, y, and z are unity with a positive sign before using the DRs of a line.
Equation of Line Passing through Two Given Points

Cartesian form




Shortest Distance between Two Lines
Slanting lines are two straight lines that are not parallel to each other or intersect. The line with the smallest distance between two skew lines will be perpendicular to both lines.



Equations of a Plane in Normal form
Vector form: r⃗ ⋅n⃗ = d is the equation of the plane in normal form, where n⃗ is a vector that is normal to the plane.
Cartesian form: The plane's equation is axe + by + cz = d, where d is the plane's distance from the origin and a, b, and c are its direction ratios.
A different equation for the plane is lx + my + nz = p, in which p is the distance of a plane from the origin and l, m, and n are the direction cosines of the perpendicular from the origin. Note: If l, m, and n are the direction cosines of the normal to the plane through the origin and d is the distance from the origin, then the foot of the perpendicular.Equation of a Plane Perpendicular to a given Vector and Passing Through a given Point

Equation of Plane Passing through Three Non-collinear Points


Coplanarity of Two Lines
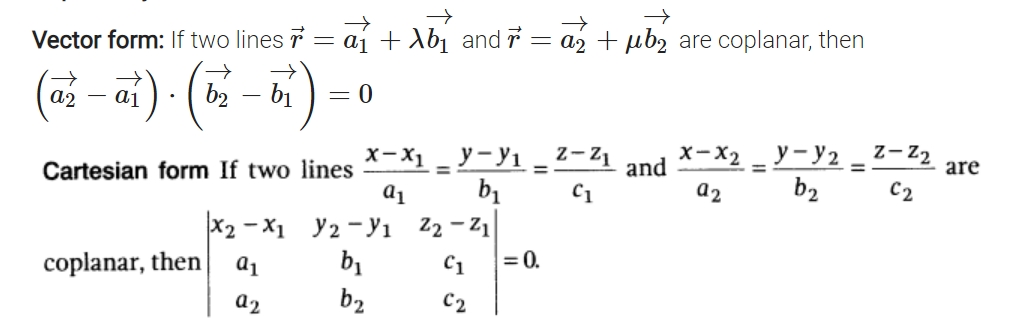
Angle between a Line and a Plane


Benefits of CBSE Class 12 Maths Notes Chapter 11
The benefits of studying CBSE Class 12 Maths Notes Chapter 11 Three Dimensional Geometry are numerous:Conceptual Clarity : The notes provide a simplified and structured explanation of complex 3D geometry concepts like lines, planes, and angles in space, helping students grasp the fundamentals effectively.
Problem-Solving Skills : The chapter improves spatial reasoning and analytical thinking, essential for solving problems related to direction cosines, distances between skew lines, and the geometry of planes.
Exam Preparation : Well-organized notes focus on key formulas and methods, making revision efficient for board exams, with stepwise explanations and illustrative examples.
Foundation for Advanced Studies : This chapter lays the groundwork for higher-level mathematics and engineering topics, such as vector calculus and analytical geometry in three dimensions.
Practical Applications : Understanding 3D geometry is crucial for real-world applications in fields like physics, architecture, and computer graphics, where spatial relationships are pivotal.
Time-Saving : Concise notes allow quick review, helping students to revise the chapter thoroughly before exams.
CBSE Class 12 Maths Notes Chapter 11 FAQs
What are the uses of three-dimensional geometry?
How is 3D geometry used in real life?
What are the fundamental concepts of 3 dimensional geometry?
What is a 3-dimensional shape called?












