

CBSE Class 12 Maths Notes Chapter 1: Relations and Functions are important for students preparing for their board exams. These notes provide a detailed overview of key concepts, including the definitions, properties, and types of relations and functions.
Understanding relations and functions is important as they form the basis for many advanced topics in mathematics. Studying these notes thoroughly will help students build a solid foundation, enhance their problem-solving skills and perform well in their exams.CBSE Class 12 Maths Notes Chapter 1 Relations and Functions Overview
CBSE Class 12 Maths Notes for Chapter 1 Relations and Functions are prepared by subject expert of Physics Wallah provide a detailed overview of key concepts in this fundamental area of mathematics. These notes cover the essential aspects of relations and functions, including their definitions, properties and various types with clear explanations and examples to aid understanding.CBSE Class 12 Maths Notes Chapter 1 PDF
The PDF link for CBSE Class 12 Maths Notes Chapter 1 Relations and Functions is available below for easy access. This detailed PDF provides a thorough overview of the chapter including definitions, properties and examples of relations and functions. With its clear explanations and structured format the PDF is an excellent resource for students to study and review the key concepts effectively. Download the PDF to enhance your understanding and preparation for the upcoming exams.CBSE Class 12 Maths Notes Chapter 1 Relations and Functions PDF
CBSE Class 12 Maths Notes Chapter 1 Relations and Functions
Here we have provided CBSE Class 12 Maths Notes Chapter 1 Relations and Functions-Relations and Functions For Class 12 Concepts
The key topics and subtopics covered in Relations and Functions for Class 12 include:- Introduction
- Types of Relations
- Types of Functions
- Composition of functions and invertible functions
- Binary operations
Relation
The concept of a relation involves linking two objects or quantities to each other. When considering two sets, a relation is established if there is a connection between the elements of these non-empty sets. Mathematically, “a relation R from a set A to a set B is a subset of the cartesian product A × B obtained by describing a relationship between the first element x and the second element y of the ordered pairs in A × B”.Types of Relations
A relation R from A to A is also stated as a relation on A, and it can be said that the relation in a set A is a subset of A × A. Thus, the empty set φ and A × A are two extreme relations. Below are the definitions of types of relations:Empty Relation
If no element of A is related to any element of A, i.e. R = φ ⊂ A × A , then the relation R in a set A is called empty relation.Universal Relation
If each element of A is related to every element of A, i.e. R = A × A , then the relation R in set A is said to be universal relation. Both the empty relation and the universal relation are sometimes called trivial relations. A relation R in a set A is called-Reflexive- if (a, a) ∈ R , for every a ∈ A,
Symmetric- if (a 1 , a 2 ) ∈ R implies that (a 2 , a 1 ) ∈ R , for all a 1 , a 2 ∈ A,
Transitive- if (a 1 , a 2 ) ∈ R and (a 2 , a 3 ) ∈ R implies that (a 1 , a 3 ) ∈ R for all a 1 , a 2 , a 3 ∈ A.
Equivalence Relation- A relation R in a set A is an equivalence relation if R is reflexive, symmetric and transitive.
Functions
A function defines a specific type of relationship between two sets, ensuring that each input is associated with exactly one output. Unlike a general relation, which can pair a single input with multiple outputs, a function mandates that each input from set A maps to a unique output in set B . This unique correspondence is fundamental in understanding and applying functions in various mathematical contexts.Types of Functions
1. One to one Function: A function f : X → Y is defined to be one-one (or injective), if the images of distinct elements of X under f are distinct, i.e., for every x 1 , x 2 ∈ X, f(x 1 ) = f(x 2 ) implies x 1 = x 2 . Otherwise, f is called many-one.
One-to-One Function Example: Each student in a class having a unique student ID.
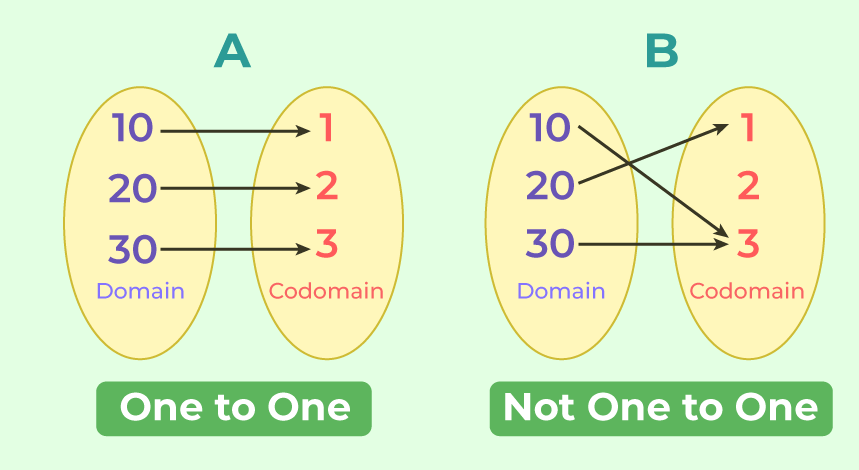
2. Many-one function
Onto Function: A function f: X → Y is said to be onto (or surjective), if every element of Y is the image of some element of X under f, i.e., for every y ∈ Y, there exists an element x in X such that f(x) = y.
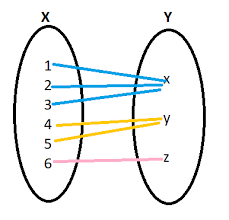
3. Onto function
One-one and Onto Function: A function f: X → Y is said to be one-one and onto (or bijective), if f is both one-one and onto.
Onto Function Example: A function that assigns students to different classes, ensuring every class has at least one student.
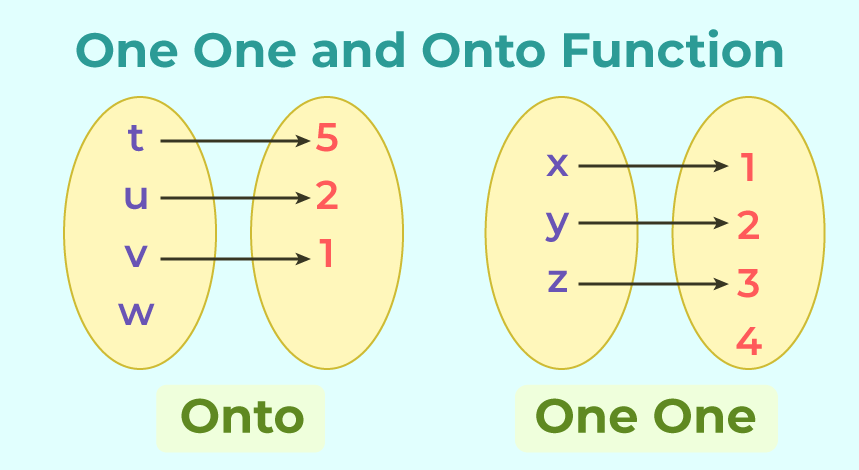
Composition of Functions
Let f: A → B and g: B → C be two functions. Then the composition of f and g, denoted by gof , is defined as the function gof: A → C given by;gof (x) = g(f (x)), ∀ x ∈ A
Invertible Functions
A function f : X → Y is defined to be invertible if there exists a function g : Y → X such that gof = I X and fog = I Y . The function g is called the inverse of f and is denoted by f –1 . An important note is that, if f is invertible, then f must be one-one and onto and conversely, if f is one-one and onto, then f must be invertible.Binary Operations
In mathematics, a binary operation on a set A is a function that combines two elements from the set to produce another element in the same set. Formally, a binary operation ∗ on is a function: This can be denoted as a∗b , where a and b are elements of A , and the result a∗b is also an element of A . Binary operations are fundamental in various fields of mathematics and are used to define algebraic structures such as groups, rings, and fields.Practice Questions of CBSE Class 12 Maths Notes Chapter 1 Relations and Functions
Here are the Practice Questions of CBSE Class 12 Maths Notes Chapter 1 Relations and Functions-Question 1: Find out whether each of the following relations are reflexive, symmetric and transitive.
(i) Relation R in the set A = {1, 2, 3…13, 14} defined as
R = {(x, y): 3x − y = 0}
(ii) Relation R in the set N of natural numbers defined as
R = {(x, y): y = x + 5 and x < 4}
(iii) Relation R in the set A = {1, 2, 3, 4, 5, 6} as
R = {(x, y): y is divisible by x}
Answer:
(i) A = {1, 2, 3 … 13, 14}
R = {(x, y): 3x − y = 0} ∴R = {(1, 3), (2, 6), (3, 9), (4, 12)} R is not reflexive since (1, 1), (2, 2) … (14, 14) ∉ R. Also, R is not symmetric as (1, 3) ∈R, but (3, 1) ∉ R. [3(3) − 1 ≠ 0] Also, R is not transitive as (1, 3), (3, 9) ∈R, but (1, 9) ∉ R. [3(1) − 9 ≠ 0] Hence, R is neither reflexive, nor symmetric, nor transitive.(ii) R = {(x, y): y = x + 5 and x < 4} = {(1, 6), (2, 7), (3, 8)}
It is seen that (1, 1) ∉ R. ∴R is not reflexive. (1, 6) ∈R But,(6, 1) ∉ R. ∴R is not symmetric. Now, since there is no pair in R such that (x, y) and (y, z) ∈R, then (x, z) cannot belong to R. ∴ R is not transitive. Hence, R is neither reflexive, nor symmetric, nor transitive.(iii) A = {1, 2, 3, 4, 5, 6}
R = {(x, y): y is divisible by x} We know that any number (x) is divisible by itself. (x, x) ∈R ∴R is reflexive. Now, (2, 4) ∈R [as 4 is divisible by 2] But, (4, 2) ∉ R. [as 2 is not divisible by 4] ∴R is not symmetric. Let (x, y), (y, z) ∈ R. Then, y is divisible by x and z is divisible by y. ∴z is divisible by x. ⇒ (x, z) ∈R ∴R is transitive. Hence, R is reflexive and transitive but not symmetric.Benefits of CBSE Class 12 Maths Notes Chapter 1 Relations and Functions
- Clear Understanding of Concepts : The notes provide a structured and detailed explanation of relations and functions making complex mathematical concepts more accessible and easier to understand. This clarity helps students grasp fundamental principles important for advanced topics.
- Comprehensive Coverage : Covering topics such as types of relations, types of functions, composition of functions, and invertible functions, these notes ensure that students receive a thorough overview of Chapter 1. This detailed approach helps in building a strong foundation in mathematics.
- Expert Preparation : Prepared by subject experts, the notes reflect a deep understanding of the curriculum and exam requirements. This expert preparation ensures that the content is accurate, relevant and based on the latest CBSE syllabus.
CBSE Class 12 Maths Notes Chapter 1 Relations and Functions FAQs
What is a relation in mathematics?
How is a function different from a general relation?
How can I determine if a function is one-to-one?
What is the importance of studying relations and functions in mathematics?












