
Stirling Formula: The Stirling Formula, named after James Stirling, serves as an approximation method for calculating the factorial of a given number (n! or Γ(n) for large values of n). This formula provides a valuable approximation, particularly beneficial for swiftly determining factorials of large numbers. While it excels in providing accurate results for larger values of 'n', it remains applicable and effective for smaller values as well.
Additionally, the Stirling Formula extends its utility beyond factorials, being applied in the context of the Gamma function and finding relevance in various areas of applied mathematics. Exploring the Stirling Formula through solved examples can further elucidate its practical applications and computational effectiveness.
The Stirling Formula is a mathematical expression used to approximate the factorial of a number, providing a value that closely aligns with the actual factorial value, often within an error margin of less than 2%. This approximation method, named after James Stirling, is used to estimate the factorial of a given number 'n'. The formula stands as a valuable tool in mathematics, offering an expression that closely approaches the real factorial value, making it highly useful for various computational and analytical purposes. The Stirling Formula is expressed as follows:
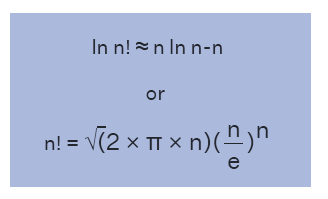
Stirling Formula Solved Examples
Example 1: Find the value of 5 factorials using the Stirling formula.
Solution:
To Find: 5 factorial.
Using Formula
n! = √(2×π×n)(n/e) n
5 fact = √(2×π×5)(5/e) 5
= 118.019
Answer: The Stirling formula approximates the value of 5 factorial to be 118.019, exhibiting an error margin of 1.66 percent.
Example 2 : Find the value of 11 factorial using the Stirling formula.
Solution:
To Find:11 factorial.
Using Stirling Formula
n! = √(2×π×n)(n/e) n
11! = √(2×π×11)(11/e) 11
= 39615625.05
Answer: The Stirling formula estimates the value of 11 factorial to be 39615625.05.
Example 3: can be approximated using Stirling's formula to find 9 ! − 7 ! 9!−7!.
By applying formula, the calculation is as follows: 9!−7!≈
(√(2π×9)× (9/e) 9 )−(√(2π×7)× (7/e) 7 )
This simplifies to: 9 ! − 7 ! ≈ 18107.57 − 1651.73
9!−7!≈18107.57−1651.73
Thus, 9 ! − 7 ! ≈ 16455.84 .
Hence, the approximate value of 9!−7! is 16455.84.
Example 4: Approximating the value of 7! using Stirling's formula. Solution: Using Stirling's formula, the approximation for 7! is calculated as follows:
7!≈ √ 2π×7 ×( 7/e ) 7
= 7 ! ≈ 19857.17
Thus, the estimated value of 7! is approximately 19857.17.
Example 5: Estimating the value of 12! using Stirling's formula.
Solution: Utilizing formula, the estimation for 12! is computed as follows:
12!≈ √2π×12 ×( 12/e ) 12
= 12 ! ≈ 479001600
Hence, the approximate value of 12! is 479001600.
Example 5: Estimating the value of 5!+4! using Stirling's formula.
Solution: Utilizing formula, the estimation for 12! is computed as follows:
5!+4! ≈ √2π×5 ×( 5/e ) 5 + √2π×4 ×( 4/e ) 4
= 5!+4! ≈ 146.30
Hence, the approximate value of 15!+4! is 146.30.
The Stirling Formula, named after mathematician James Stirling, stands as a powerful approximation method for factorials, offering a close estimate to the actual values, particularly for large numbers, with an error margin often less than 2%. This formula, expressed as n! ≈ √(2πn) * (n/e)^n, not only accurately estimates factorials but also finds wide applications in various fields of applied mathematics.
Through examples showcasing its application, the Stirling Formula demonstrates its practical utility in swiftly and accurately approximating factorial values, aiding in computational and analytical endeavors. Its versatility caters to both small and large values of 'n', making it an invaluable tool in mathematical calculations and analyses. Overall, the Stirling Formula stands as a cornerstone in approximation techniques, facilitating efficient estimations of factorials and finding relevance in diverse mathematical applications.
Explore Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your Maths knowledge. and build a strong foundation.
| Related Links | |
| T-Test Formula | Trajectory Formula |
| U Substitution Formula | Vertex Formula |
Stirling Formula FAQs
What is the Stirling Formula?
When is the Stirling Formula used?
In what fields does the Stirling Formula find application?
How accurate is the Stirling Formula?










