
In the realm of mathematics, a Hyperbola holds a significant place as a conic section, which takes shape when a plane intersects a double cone. It's important to note that this intersection doesn't necessarily occur at the center of the cone. Hyperbolas exhibit symmetry along their conjugate axis and exhibit several similarities to ellipses. Key concepts such as foci, directrix, latus rectum, and eccentricity apply to hyperbolas as well. Let's delve into a more detailed exploration of hyperbolas, including their definition, formulas, derivation of these formulas, and the standard forms of hyperbolas through solved examples.
A hyperbola is defined as a set of points where the absolute difference of distances to two fixed points, called the foci, is constant. This difference is known as the focal width, and it defines the shape of the hyperbola.
What is Hyperbola Formula?
Your description of a hyperbola is accurate and provides a clear understanding of this mathematical concept. Hyperbolas indeed consists of two distinct branches, each of which resembles an infinite bow, and these branches are mirror images of each other. The fundamental property of a hyperbola is that it's defined as a set of points where the absolute difference of distances from any point on the hyperbola to two fixed foci is a constant value. This difference is typically taken as the distance from the farther focus to the point minus the distance from the nearer focus to the point. Mathematically, it's represented as:
PF - PF' = 2a.
- P(x, y) is a point on the hyperbola.
- F and F' are the two foci of the hyperbola.
- PF is the distance from the point P to the focus F.
- PF' is the distance from the point P to the focus F'.
- 2a is the constant difference between these distances.
Understanding this property is essential for working with hyperbolas in geometry and algebra, and it provides a geometric interpretation of the hyperbola as the locus of points that satisfy this specific distance condition. This property can be used to derive the standard equation of a hyperbola, as mentioned in the previous response.
Hyperbola Formula Definition
A hyperbola is indeed a conic section that forms when a plane intersects a double right circular cone at a particular angle, ensuring that both halves of the cone are intersected. The result of this intersection is two distinct unbounded curves, each of which is a mirror image of the other. These two curves, known as branches, make up the hyperbola. This geometric definition helps visualize and understand the fundamental nature of a hyperbola as a pair of infinite, mirror-symmetric curves.
Parts of a Hyperbola
- Foci of a hyperbola: A hyperbola has two foci, and their coordinates are F(c, 0) and F'(-c, 0).
- Center of the Hyperbola: The midpoint of the line that connects the two foci is referred to as the center of the hyperbola.
- Major Axis: The length of the major axis of the hyperbola is 2a units.
- Minor Axis: The length of the minor axis of the hyperbola is 2b units.
- Vertices: The points where the hyperbola intersects its axes are known as the vertices. For a hyperbola, the vertices are located at (a, 0) and (-a, 0).
- Latus Rectum of the Hyperbola: The latus rectum is a line drawn perpendicular to the transverse axis of the hyperbola and passes through the foci. The length of the latus rectum of the hyperbola is 2b^2/a.
- Transverse Axis: The line that passes through the two foci and the center of the hyperbola is called the transverse axis.
- Conjugate Axis: The line that passes through the center of the hyperbola and is perpendicular to the transverse axis is known as the conjugate axis.
- Eccentricity of the Hyperbola (e > 1): The eccentricity is the ratio of the distance between the focus and the center of the hyperbola to the distance between the vertex and the center of the hyperbola. The focus is at a distance of 'c' units from the center, and the vertex is at a distance of 'a' units, so the eccentricity is given by e = c/a.
Also Check – Line and Angles Formula
Hyperbola Formula Equation
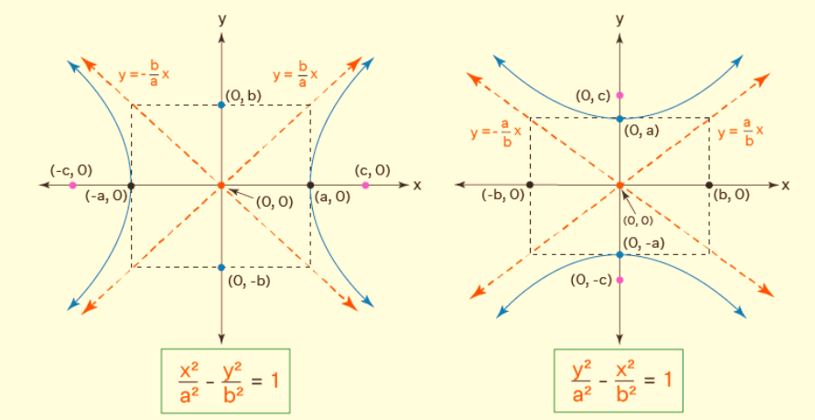
The equation below represents the general equation of a hyperbola, where the x-axis corresponds to the transverse axis of the hyperbola, and the y-axis corresponds to the conjugate axis of the hyperbola.
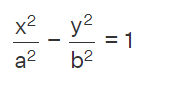
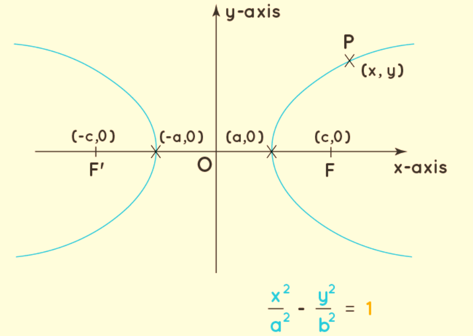
In the following sections, we will delve into a detailed explanation of the standard form of the hyperbola equation and its derivation.
Also Check – Line and Angles Formula
Standard Equation of Hyperbola
There are two standard equations for hyperbolas, each based on the orientation of the transverse axis and the conjugate axis. The first standard equation of the hyperbola places the transverse axis along the x-axis, with the conjugate axis aligned with the y-axis.
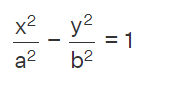
Conversely, the second standard equation of the hyperbola positions the transverse axis along the y-axis, while the conjugate axis aligns with the x-axis.
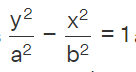
The following image illustrates these two standard forms of hyperbola equations.
Derivation of Hyperbola Formula Equation
let's proceed with squaring both sides of the equation to continue with the derivation:
Given:
PF' - PF = 2a
Let P have coordinates (x, y) and the foci be F(c, 0) and F'(-c, 0).
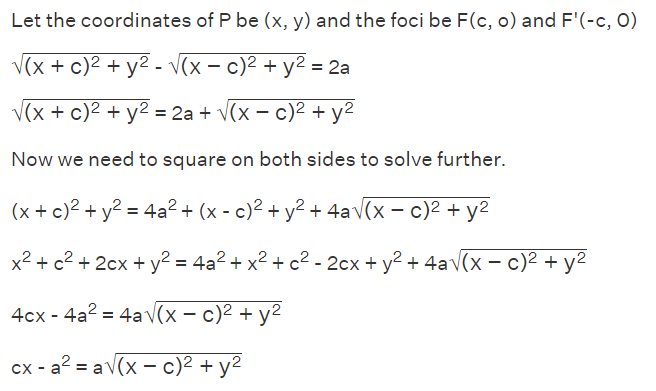
Now, squaring both sides of the equation:
(PF' - PF)^2 = (2a)^2
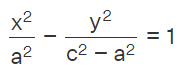
This simplifies to:
(PF' - PF)^2 = 4a^2
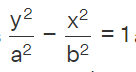
We have now squared the equation, and we can continue to work with it for further analysis and derivation.
Squaring on both sides and simplifying, we have.
Since, we have c 2 = a 2 + b 2 , we can put this value in the above equation.
Therefore, the standard equation of the Hyperbola is derived.
Also Check – Congruence of triangles formula
Hyperbola Formula
Hyperbola is an open curve that has two branches that look like mirror images of each other. For any point on any of the branches, the absolute difference between the point from foci is constant and equals to 2a, where a is the distance of the branch from the center. The Hyperbola formula helps us to find various parameters and related parts of the hyperbola such as the equation of hyperbola, the major and minor axis, eccentricity, asymptotes, vertex, foci, and semi-latus rectum.
A hyperbola is a curve with two branches that are symmetric mirror images of each other. For any point on either branch, the absolute difference between its distance from the foci is constant and equal to 2a, where 'a' represents the distance from the branch to the center. Hyperbola formulas help us calculate various parameters and related aspects of the hyperbola, such as its equation, major and minor axes, eccentricity, asymptotes, vertices, foci, and semi-latus rectum.

Example: Given the hyperbola equation (x - 5) 2 /4 2 - (y - 2) 2 / 2 2 = 1 let's use hyperbola formulas to determine the lengths of the major and minor axes.
Solution: Using the hyperbola formula for the length of the major and minor axes, we have Length of the major axis = 2a and Length of the minor axis = 2b.
Length of the major axis = 2 × 4 = 8 units, and Length of the minor axis = 2 × 2 = 4 units.
Answer: The length of the major axis is 8 units, and the length of the minor axis is 4 units.
Graph of Hyperbola
Hyperbolas indeed share common features, and each one consists of two separate curves, each with its own vertex and focus. The transverse axis is the axis that passes through both vertices and foci, and the conjugate axis is perpendicular to it. When working with hyperbolas, it's essential to understand their standard forms and how to transform equations into standard form when necessary.
Graphing hyperbolas using standard equations is a fundamental approach to visualize their shapes and characteristics. These standard forms provide a clear representation of the hyperbola and its various components, such as the vertices, foci, asymptotes, and the relationships between them.
When the equation of a given hyperbola is not in standard form, completing the square is a useful technique to transform it into the standard form for better analysis and graphing.
Studying the different parts of a hyperbola within the context of its standard equations is crucial for understanding and working with these curves effectively.

Here,
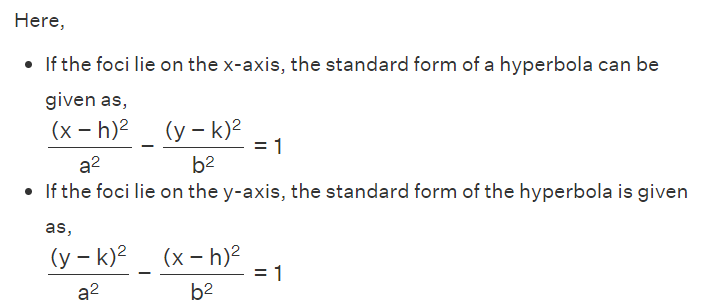
- If the foci lie on the x-axis, the standard form of a hyperbola can be given as,
- Coordinates of the center: (h, k).
- Coordinates of vertices: (h+a, k) and (h - a,k)
- Co-vertices correspond to b, the ” minor semi-axis length”, and coordinates of co-vertices: (h,k+b) and (h,k-b).
- Foci have coordinates (h+c,k) and (h-c,k). The value of c is given as, c 2 = a 2 + b 2 .
- Slopes of asymptotes: y = ±(b/a)x.
Properties of a Hyperbola
Asymptotes: Hyperbolas have a pair of straight lines known as asymptotes. These lines are drawn parallel to the hyperbola and are assumed to touch the hyperbola at infinity. The equations of the asymptotes for a hyperbola are y = bx/a and y = -bx/a.
Rectangular Hyperbola: When a hyperbola has both the transverse axis and the conjugate axis of the same length, it's called a rectangular hyperbola. In this case, 2a = 2b, or simply a = b. The equation of a rectangular hyperbola is x 2 - y 2 = a 2 .
Parametric Coordinates: Points on a hyperbola can be represented using parametric coordinates (x, y) = (asecθ, btanθ). These parametric coordinates satisfy the equation of the hyperbola.
Auxiliary Circle: An auxiliary circle is drawn with the endpoints of the transverse axis of the hyperbola as its diameter. The equation of the auxiliary circle of the hyperbola is x 2 + y 2 = a 2 .
Director Circle: The director circle is the locus of the point of intersection of perpendicular tangents to the hyperbola. Its equation is x 2 + y 2 = a 2 - b 2 .
Understanding these properties and concepts is crucial for a comprehensive grasp of hyperbolas and their geometric and algebraic characteristics.
| Related Links | |
| Fibonacci Sequence Formula | Eulers Formula |
| Exponential Formula | Factorial Formula |
Hyperbola Formula FAQs
What is a hyperbola?
What is the eccentricity of a hyperbola?
What is the formula for the eccentricity of a hyperbola?
Give the standard equation of the hyperbola.
What do you mean by the transverse axis of a hyperbola?










