
Sample Mean Formula: The sample mean, often denoted as x̄ (pronounced as "x-bar"), is a statistical tool that is used to measure the average value of a sample data set. It provides an estimate of the population mean when it is not possible to collect data from an entire population. The sample mean is a important concept in statistics and is used to make inferences about populations based on sample data. It serves as a point estimate of the population mean.
The sample mean is calculated by summing up all the values in a sample and dividing by the number of data points in that sample. It is a key step in many statistical analyses and hypothesis testing.
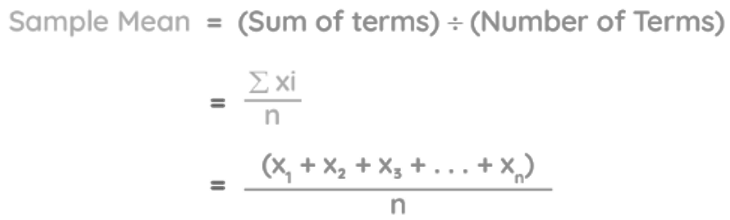
The sample mean formula can be represented as:
x̄ = (Σx) / n
Where:
x̄ is the sample mean.
Σx represents the sum of all values in the sample.
n is the number of data points in the sample.
Applications of the sample mean include estimating population parameters, making predictions, conducting hypothesis tests, and assessing the central tendency of a data set. It is a fundamental tool in statistics for drawing conclusions about populations based on the information available from a sample.
What Is Sample Mean Formula?
The sample mean formula is indeed used to determine the average value of a given sample data set. This formula allows you to find the sample mean by taking the sum of all the values in the sample and dividing it by the total number of terms in the sample. In mathematical terms, the sample mean formula is given as:
Sample Mean (x̄) = (Sum of Sample Values) / (Number of Sample Values)
This formula provides a straightforward way to calculate the average or central value of a sample, making it a fundamental concept in statistics for summarizing and analyzing data.
Sample Mean Formula
The sample mean formula, as expressed, is indeed a fundamental concept in statistics, used to calculate the average value of a sample data set. The formula is represented as follows:
Sample Mean = (Sum of terms) ÷ (Number of Terms) = Σxi / n
Where:
Σxi represents the sum of all terms in the sample.
n = number of terms in the given sample.
Sample Mean Formula Applications
The sample mean formula finds applications in various fields and scenarios, such as:
- Descriptive Statistics: The sample mean is commonly used to describe the central tendency of a data set, providing an average value that summarizes the data.
- Inferential Statistics: In hypothesis testing and confidence interval estimation, the sample mean serves as an estimator for the population mean, allowing us to make conclusions about the whole population based on a given sample.
- Quality Control: In manufacturing and production, the sample mean can be used to monitor the quality of products by comparing sample measurements to a target value.
- Market Research: When conducting surveys or collecting data from a sample of consumers, the sample mean helps estimate the average preferences, behaviors, or opinions of the larger population.
- Academic Research: Researchers use the sample mean to analyze data from samples, assess outcomes of experiments, and draw conclusions about a broader population.
- Business Decision-Making: Business analysts often rely on the sample mean to assess key performance metrics, such as sales revenue, customer satisfaction, or employee productivity.
- Finance: Investors and financial analysts may use the sample mean to assess the performance of a sample portfolio and make inferences about broader market trends.
- Medical Research: In clinical trials and medical studies, the sample mean is used to analyze patient data, assess treatment outcomes, and draw conclusions about a larger patient population.
- Environmental Studies: Environmental scientists use the sample mean to analyze data related to environmental variables, such as pollution levels, temperature readings, and species populations.
The sample mean formula is a fundamental tool in statistics that enables the analysis of data, facilitates decision-making, and supports various research and practical applications across multiple fields.
Sample Mean Formula Examples
Example 1: Finding the Sample Mean of Exam Scores
Suppose you have the following exam scores for a sample of 10 students: 85, 92, 78, 89, 95, 70, 88, 79, 91, and 84. To calculate the sample mean:
Sample Mean (x̄) = (Sum of Sample Scores) / (Number of Scores)
x̄ = (85 + 92 + 78 + 89 + 95 + 70 + 88 + 79 + 91 + 84) / 10
x̄ = 871 / 10
x̄ = 87.1
The sample mean of the exam scores is 87.1.
Example 2: Determining the Sample Mean of Daily Temperatures
Suppose you recorded the daily temperatures (in degrees Fahrenheit) for a sample of 7 days: 72, 76, 74, 68, 70, 73, and 75. To find the sample mean:
Sample Mean (x̄) = (Sum of Daily Temperatures) / (Number of Days)
x̄ = (72 + 76 + 74 + 68 + 70 + 73 + 75) / 7
x̄ = 508 / 7
x̄ ≈ 72.57
The sample mean of the daily temperatures is approximately 72.57 degrees Fahrenheit.
Example 3: Calculating the Sample Mean of Test Scores
Consider a sample of test scores from 15 students: 88, 95, 79, 92, 85, 91, 76, 90, 84, 87, 94, 89, 82, 78, and 93. To determine the sample mean:
Sample Mean (x̄) = (Sum of Test Scores) / (Number of Students)
x̄ = (88 + 95 + 79 + 92 + 85 + 91 + 76 + 90 + 84 + 87 + 94 + 89 + 82 + 78 + 93) / 15
x̄ = 1271 / 15
x̄ ≈ 84.73
The sample mean of the test scores is approximately 84.73.
These examples demonstrate how to use the sample mean formula to calculate the average value of data in various sample sets. The sample mean is a crucial statistical measure for summarizing and analyzing sample data.
| Related Links | |
| Perimeter of a Kite Formula | Perpendicular Line Formula |
| Platonic Solids Formula | Point of Intersection Formula |
Sample Mean Formula FAQs
Q1. What is the sample mean, and how is it different from the population mean?
Q2. How is the sample mean formula calculated?
Q3. When should I use the sample mean formula?
Q4. Can the sample mean be used to make inferences about the population mean?
Q5. Is the sample mean sensitive to outliers in the data?










