ICSE Class 8 Maths Selina Solutions Chapter 10 Direct and Inverse Variations

ICSE Class 8 Maths Selina Solutions Chapter 10: These kinds of situations, where a change in one quantity causes a change in another, are common in real life. For instance, if an automobile's speed is raised, it will take less time to travel the same distance. Let's use one more example: to expedite the completion of a building project, we must assign additional labor.

ICSE Class 8 Maths Selina Solutions Chapter 10 Overview

ICSE Class 8 Maths Selina Solutions Chapter 10 PDF

ICSE Class 8 Maths Selina Solutions Chapter 10 PDF

ICSE Class 8 Maths Selina Solutions Chapter 10

Question 2.

If x and y vary directly, find the values of x,y , and z.

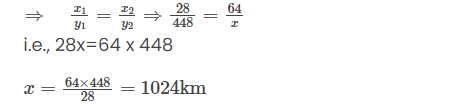
Question 4.

For 100km, a taxi charges ₹ 1,800. How much will it charge for a journey of 120 km?

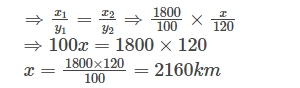
Question 5.

If 27 identical articles cost ₹ 1,890, how many articles can be bought for ₹ 1,750?

Solution:- Let x number of articles be purchased in ₹ 1750

Cost (₹)	1890	1750
No. of articles	27	X

Since it is a case of direct variation

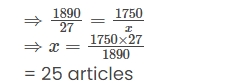
Question 6.

7kg of rice costs Rs.1,120. How much rice can be bought for Rs.3,680?

Solution: Rice: Cost : Rice: Cost 7kg: 1120 :: x kg : 3680

Question 7.

6 notebooks cost ₹ 156, find the cost of 54 such note-books.

Solution:- Notebooks: cost:: notebooks: cost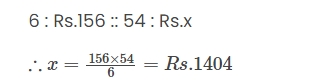

Question 8.

22 men can dig a 27 m-long trench in one day. How many men should be employed for digging a 135 m-long trench of the same type in one day?

Solution:- Men: length trench:: men: length of trench 22 : 27m :: x : 135m (Expressing in ratios)

Question 9.

If the total weight of 11 identical articles is 77 kg, how many articles of the same type would weigh 224 kg?

Solution:- No. of: weight :: no. of articles: weight Articles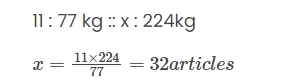

Question 10.

A train is moving at a uniform speed of 120km per hour.

(i) How far will it travel in 36 minutes? Solution:- Speed of train in 60 minutes =120 km

Question 1.

Check whether x and y vary inversely or not.

(i)

x	4	3	12	1
y	6	8	2	24

Solution:- x and y are inversely proportional Then xy are equal. (i)

Question 2.

If x and y vary inversely, find the values of 1, m, and n:

(i)

x	4	8	2	32
y	4	l	m	n

Solution:- ∵ x and y are inversely proportional ∴xy is equal Now,

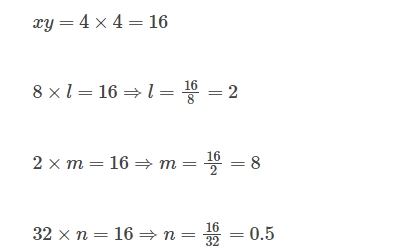
(ii)

x	24	32	m	16
y	l	12	8	n

Solution:- ∵x and y are inversely proportional ∴xy is equal Now,

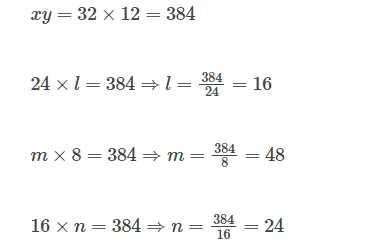
Question 3.

36 men can do a piece of work in 7 days. How many men will do the same work in 42 days?

Solution:- Men: Days :: Men: Days 36 : 7 : x : 42 ∴ By inverse proportional

Question 4.

12 pipes, all of the same size, fill a tank in 42 minutes. How long will it take to fill the same tank, if 21 pipes of the same size are used?

Solution:-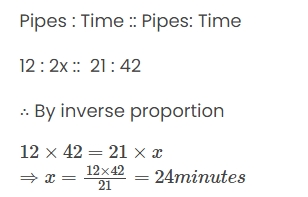

Question 5.

In a fort 150 men had provisions for 45 days. After 10 days, 25 men left the fort. How long would the food last at the same rate?

Solution:-

Benefits of ICSE Class 8 Maths Selina Solutions Chapter 10

Concept Clarity : The chapter provides clear explanations and examples to help students understand the concepts of direct and inverse proportions. This clarity enables them to grasp how quantities relate to each other and how changes in one affect the other.

Problem-Solving Skills : By practicing problems related to direct and inverse variations, students develop strong problem-solving skills. They learn to apply mathematical formulas and methods to analyze and solve problems involving these types of relationships.

Real-World Applications : Understanding direct and inverse proportions helps students recognize these relationships in real-life situations. This practical knowledge can be applied to fields such as science, economics, engineering, and everyday decision-making.

Foundation for Advanced Topics : Mastery of direct and inverse proportions lays a solid foundation for more advanced topics in mathematics and science. It prepares students for higher-level studies where such proportional relationships are fundamental.

Logical Thinking : Working with direct and inverse proportions requires logical thinking and reasoning skills. Students learn to analyze problems, formulate strategies, and justify their solutions, which enhances their overall cognitive development.

Preparation for Exams : Since direct and inverse proportions are frequently tested in exams, studying this chapter thoroughly ensures that students are well-prepared to tackle related questions confidently.