
ICSE Class 8 Maths Selina Solutions Chapter 18: In ICSE Class 8 Maths Selina Solutions Chapter 18, "Constructions," students learn important techniques for constructing geometric figures using basic tools like a ruler, compass, and protractor.
This chapter focuses on practical skills such as bisecting angles, constructing perpendicular and parallel lines, drawing triangles based on given measurements, and constructing various types of quadrilaterals. Through step-by-step instructions and clear illustrations, students gain hands-on experience in creating accurate geometric shapes, reinforcing their understanding of geometric concepts and preparing them for more advanced topics in mathematics. This chapter not only builds technical proficiency but also cultivates problem-solving abilities by applying precise construction methods to solve practical geometry problems.ICSE Class 8 Maths Selina Solutions Chapter 18 Constructions Overview
The solutions for ICSE Class 8 Maths Selina Solutions Chapter 18, "Constructions," are created by subject experts of Physics Wallah. The solutions give clear, step-by-step instructions on how to do tasks like dividing angles in half, drawing lines that are perpendicular or parallel, and making triangles and quadrilaterals based on specific measurements. By using these solutions, students can practice and improve their skills in geometry, understand how to solve construction problems, and feel more prepared for their exams.Constructions
In the context of geometry, "Constructions" refer to the methodical creation of geometric figures using basic tools such as a ruler, compass, and protractor. These tools allow mathematicians and students to accurately reproduce shapes and angles based on specific instructions or conditions. Here is a detailed overview of some common constructions:Bisecting a Line Segment :
- To find the midpoint of a line segment, use a compass to draw arcs from both endpoints. Where the arcs intersect marks the midpoint.
Bisecting an Angle :
- To divide an angle into two equal parts, use a compass to draw arcs from each side of the angle. Where the arcs intersect inside the angle marks the bisector.
Constructing Perpendicular Lines :
- To draw a line perpendicular to another at a specific point, use a compass to draw arcs of equal radius from that point on both sides of the line. Connect the intersections of the arcs to create the perpendicular line.
Constructing Parallel Lines :
- To create a line parallel to another through a specific point, use a compass to measure equal distances on the original line from the point. Draw arcs with these distances and connect corresponding points on the arcs.
Constructing Triangles :
- Given specific measurements (such as side lengths and angles), use compass and ruler constructions to accurately draw triangles of different types (equilateral, isosceles, scalene).
Constructing Quadrilaterals :
- Depending on the given conditions (like side lengths and angles), use construction methods to draw quadrilaterals such as parallelograms, rectangles, squares, rhombuses, and trapeziums.
ICSE Class 8 Maths Selina Solutions Chapter 18 PDF
You can find the PDF link for ICSE Class 8 Maths Selina Solutions Chapter 18 "Constructions" below. This PDF provides detailed solutions and explanations on how to perform geometric constructions using basic tools like rulers, compasses, and protractors. It is a valuable resource for students looking to practice and master construction techniques in geometry, helping them to understand and apply these skills effectively.ICSE Class 8 Maths Selina Solutions Chapter 18 Constructions PDF
ICSE Class 8 Maths Selina Solutions Chapter 18 Constructions
Below we have provided ICSE Class 8 Maths Selina Solutions Chapter 18 Constructions for the ease of the students –Question 1.
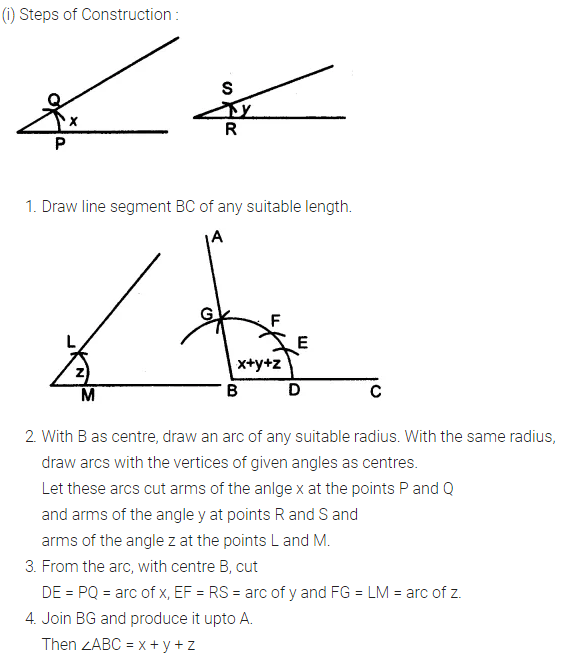
Given below are the angles x and y. Without measuring these angles, construct :
(i) ∠ABC = x + y
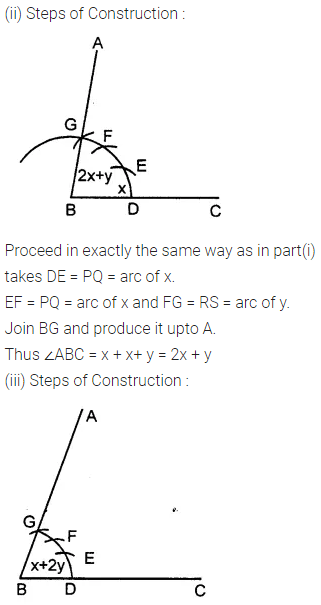
(ii) ∠ABC = 2x + y
(iii) ∠ABC = x + 2y
Without measuring these angles, construct :
(i) ∠ABC = x + y
(ii) ∠ABC = 2x + y
(iii) ∠ABC = x + 2y
Solution:


Solution:
Question 3.
Construct angle ABC = 90°. Draw BP, the bisector of angle ABC. State the measure of angle PBC.Solution:

Question 4.
Draw angle ABC of any suitable measure. (i) Draw BP, the bisector of angle ABC. (ii) Draw BR, the bisector of angle PBC and draw BQ, the bisector of angle ABP. (iii) Are the angles ABQ, QBP, PBR and RBC equal? (iv) Are the angles ABR and QBC equal ? Solution: Steps of Construction : 1. Construct any angle ABC
2. With B as centre, draw an arc EF meeting BC at E and AB at F.
3. With E, F as centres draw two arc of equal radii meeting each other at the point P.
4. Join BP. Then BP is the bisector of
∠
ABC
∴
∠
ABP
=
∠
PBC
=
1
2
∠
ABC
5. Similarly draw BR, the bisector of
∠
PBC and draw BQ as the bisector of
∠
ABP
[With the same method as in steps 2, 3]
6. Then
∠
ABQ=
∠
QBP=
∠
PBR=
∠
RBC
7.
∠
ABR=
3
4
∠
ABC and
∠
QBC=
3
4
∠
ABC
∴
∠
ABR=
∠
QBC.
1. Construct any angle ABC
2. With B as centre, draw an arc EF meeting BC at E and AB at F.
3. With E, F as centres draw two arc of equal radii meeting each other at the point P.
4. Join BP. Then BP is the bisector of
∠
ABC
∴
∠
ABP
=
∠
PBC
=
1
2
∠
ABC
5. Similarly draw BR, the bisector of
∠
PBC and draw BQ as the bisector of
∠
ABP
[With the same method as in steps 2, 3]
6. Then
∠
ABQ=
∠
QBP=
∠
PBR=
∠
RBC
7.
∠
ABR=
3
4
∠
ABC and
∠
QBC=
3
4
∠
ABC
∴
∠
ABR=
∠
QBC.
Question 5.
Draw a line segment AB of length 5.3 cm. Using two different methods bisect AB.Solution:
 Question 6.
In each of the following, draw perpendicular through point P to the line segment AB :
Question 6.
In each of the following, draw perpendicular through point P to the line segment AB :

Solution:

Question 7.
Draw a line segment AB = 5.5 cm. Mark a point P, such that PA = 6 cm and PB = 4.8 cm. From the point P, draw a perpendicular to AB.Solution:

Question 8.
Draw a line segment AB = 6.2 cm. Mark a point P in AB such that BP = 4 cm. Through point P draw perpendicular to AB.Solution:

Question 9.
Draw a line AB = 6 cm. Mark a point P any where outside the line AB. Through the point P, construct a line parallel to AB.Solution :
Steps of construction : 1. Draw a line AB = 6 cm
2. Take any point Q on the line AB and join it with the given point P.
3. At point P, construct
∠
CPQ =
∠
PQB
4. Produce CP upto any point D.
Thus, CPD is the required parallel line.
1. Draw a line AB = 6 cm
2. Take any point Q on the line AB and join it with the given point P.
3. At point P, construct
∠
CPQ =
∠
PQB
4. Produce CP upto any point D.
Thus, CPD is the required parallel line.
Question 10.
Draw a line MN = 5.8 cm. Locate a point A which is 4.5 cm from M and 5 cm from N. Through A draw a line parallel to line MN.Solution:

Question 11.
Draw a straight line AB = 6.5 cm. Draw another line which is parallel to AB at a distance of 2.8 cm from it.Solution:
Steps of construction : 1. Draw a straight line AB = 6.5 cm
2. Taking point A as centre, draw an arc of radius 2.8 cm.
3. Taking B as centre, drawn another arc of radius 2.8 cm.
4. Draw a line CD which touches the two arcs drawn.
Thus CD is the required parallel line.
1. Draw a straight line AB = 6.5 cm
2. Taking point A as centre, draw an arc of radius 2.8 cm.
3. Taking B as centre, drawn another arc of radius 2.8 cm.
4. Draw a line CD which touches the two arcs drawn.
Thus CD is the required parallel line.
Question 12.
Construct an angle PQR = 80°. Draw a line parallel to PQ at a distance of 3 cm from it and another line parallel to QR at a distance of 3.5 cm from it. Mark the point of intersection of these parallel lines as A.Solution:
Steps of construction: 1. Construct ∠𝑃𝑄𝑅=80𝑜 2. Taking 𝑃 as center construct an arc of radius 2𝑐𝑚. 3. Again with 𝑄 as center, Construct another arc of radius 2𝑐𝑚. Then 𝐵𝑀 is a line which touches the two arcs. Then 𝐵𝑀 is a line parallel to 𝑃𝑄. 4. Taking 𝑄 as center, construct an arc of radius 3.5𝑐𝑚. Taking 𝑅 as center construct another arc of radius 3.5. Construct a line 𝐻𝐶 which touches these two arcs. Let these two parallel lines intersect at 𝐴.Question 13.
Draw an angle ABC = 60°. Draw the bisector of it. Also draw a line parallel to BC a distance of 2.5 cm from it. Let this parallel line meet AB at point P and angle bisector at point Q. Measure the length of BP and PQ. Is BP = PQ?Solution:
Steps of construction : 1. Draw ∠ ABC = 60 ∘ 2. Draw BD, the bisector of ∠ ABC. 3. Taking B as centre, draw an arc of radius 2.5 cm. 4. Taking C as centre, draw another arc of radius 2.5 cm. 5. Draw a line MN which touches these two arcs drawn. Then MN is the required line parallel to BC. 6. Let this line MN meets AB at P and bisector BD at Q. 7. Measure BP and PQ. By measurement we see BP = PQ.Question 14.
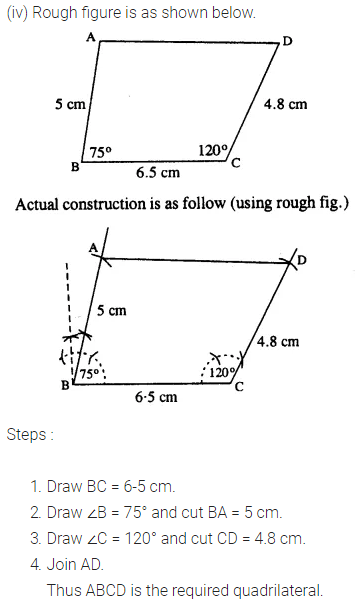
Construct a quadrilateral ABCD; if: (i) AB = 4.3 cm, BC = 5.4, CD = 5 cm, DA = 4.8 cm and angle ABC = 75°. (ii) AB = 6 cm, CD = 4.5 cm, BC = AD = 5 cm and ∠BCD = 60°. (iii) AB = 8 cm, BC = 5.4 cm, AD = 6 cm, ∠A = 60° and ∠B = 75°. (iv) AB = 5 cm, BC = 6.5 cm, CD =4.8 cm, ∠B = 75° and ∠C = 120°. (v) AB = 6 cm = AC, BC = 4 cm, CD = 5 cm and AD = 4.5 cm. (vi) AB = AD = 5cm, BD = 7 cm and BC = DC = 5.5 cm Solution:



Benefits of ICSE Class 8 Maths Selina Solutions Chapter 18 Constructions
- Understanding Geometry : By practicing constructions, students gain a deeper understanding of geometric principles such as angles, symmetry, and properties of shapes like triangles and quadrilaterals.
- Problem-Solving Skills : Constructing geometric figures requires logical thinking and problem-solving skills, helping students develop analytical abilities.
- Visualizing Concepts : It enhances students ability to visualize and manipulate geometric shapes, which is crucial for spatial reasoning and understanding complex geometric relationships.
- Preparation for Advanced Topics : Mastering constructions lays a strong foundation for more advanced topics in geometry and mathematics, preparing students for higher-level studies.
- Exam Preparation : The solutions provide step-by-step guidance on how to perform constructions, helping students prepare effectively for exams by practicing construction-based problems.
ICSE Class 8 Maths Selina Solutions Chapter 18 FAQs
What are constructions in geometry?
Why are constructions important in mathematics?
What tools are commonly used in geometric constructions?
What skills do constructions help develop?










