ICSE Class 8 Maths Selina Solutions Chapter 3 Squares and Square Roots
Neha Tanna9 Jul, 2024
Share
ICSE Class 8 Maths Selina Solutions Chapter 3: Different techniques of computing the square roots of numbers are explained in Class 8 Maths, Chapter 3, "Square and Square Roots." Students must have a basic understanding of squares before moving on to learning about square roots. All it takes to find the square of any number is to multiply it by itself.
For instance: Three is the square root of nine since nine is obtained by multiplying three by itself. The squares of whole numbers, like 1, 4, 9, 16, etc., are the perfect squares. Positive numbers have two square roots to find the square roots of; a positive square root (referred to as the principal square root) and a negative square root. To do well on the yearly exam, Class 8 ICSE students should practice problems from the Selina textbook. Students can evaluate their errors and weak points and double-check their answers with the aid of the ICSE Class 8 Maths Selina Solutions PDF. However, they must have a firm grasp of the concept of "Square and Square Roots" before they can begin answering the questions.ICSE Class 8 Maths Selina Solutions Chapter 3 Overview
ICSE Class 8 Maths Selina Solutions Chapter 3 on squares and square roots provides clear and detailed explanations for students to understand the fundamental concepts thoroughly. Each topic is systematically covered with step-by-step solutions, ensuring clarity in learning. The solutions not only help in solving textbook exercises but also offer additional practice questions to strengthen problem-solving skills. With accurate explanations and comprehensive coverage, these solutions are designed to aid students in mastering the concepts of squares and square roots effectively, preparing them confidently for exams and future mathematical challenges.ICSE Class 8 Maths Selina Solutions Chapter 3 PDF
Here we have provided ICSE Class 8 Maths Selina Solutions Chapter 3 for the ease of students so that they can just download the pdf and use it easily without the internet. These ICSE Class 8 Maths Selina Solutions Chapter 3 will help students understand the chapter better.ICSE Class 8 Maths Selina Solutions Chapter 3 PDF
ICSE Class 8 Maths Selina Solutions Chapter 3 Squares and Square Roots
Here we have provided ICSE Class 8 Maths Selina Solutions Chapter 3 for the ease of students so that they can prepare better for their upcoming exams -Question 1.
Find the square of:
(i) 59 (ii) 6.3 (iii) 15 Solution: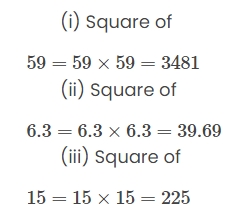
Question 2. By splitting into prime factors, find the square root of:
(i) 11025
Solution:
(ii) 396900
Solution:
(iii) 194481
Solution:
Question 3.
(i) Find the smallest number by which 2592 is multiplied so that the product is a perfect square.
Solution:
(ii) Find the smallest number by which 12748 be multiplied so that the product is a perfect square.
Solution:
Question 4.
Find the smallest number by which 10368 is divided so that the result is a perfect square. Also, find the square root of the resulting numbers.
Solution:
Question 5. Find the square root of:
Question 6. Evaluate
Question 7. Evaluate:
Question 8. A man, after a tour, finds that he had spent the day as many rupees as the number of days he had been on tour. How long did his tour last, if he had spent in all 1,296?
Solution: Let the number of days he had spent =x Number of rupees spent in each day =x Total money spent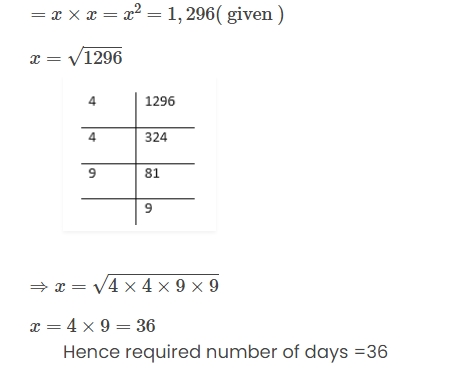
Question 9. Out of 745 students, a maximum is to be arranged in the school field for a PT. display, such that the number of rows is equal to the number of columns. Find the number of rows if 16 students were left out after the arrangement.
Solution: Total number of students =745 Students left after standing in arrangement =16 No. of students who were to be arranged = 745-16=729 The number of rows = No. of students in each row No. of rows
Question 10. 13 and 31 are a strange pair of numbers such that squares 169 and 961 also mirror images of each other. Find two more such pairs.
Solution: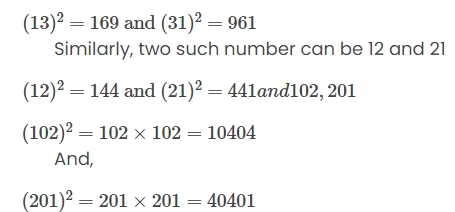
ICSE Class 8 Maths Selina Solutions Chapter 3 Exercise 3B
Question 1. Find the square root of:
(i) 4761
Solution:
Question 2. Find the square root of:
(i) 4.2025
Solution:
Required square root =2.05
(ii) 531.7636
Solution:
Required square root =23.06
(iii) 0.007225
Solution:
Required square root =0.085
Question 3. Find the square root of:
(i) 245 correct to two places of decimal.
Solution:
Benefits of ICSE Class 8 Maths Selina Solutions Chapter 3
Selina Solutions for ICSE Class 8 Maths Chapter 3 on squares and square roots offers several benefits for students:Comprehensive Coverage : The solutions provide a thorough explanation of each topic covered in the chapter. This includes definitions, properties, and practical examples related to squares and square roots.
Step-by-Step Approach : Each problem is solved in a step-by-step manner, making it easier for students to understand the logic and methodology behind solving similar problems independently.
Clarity and Accuracy : The solutions ensure clarity in concepts and accuracy in calculations, helping students grasp the nuances of squares and square roots effectively.
Practice Material : Besides solutions to textbook exercises, Selina Solutions often includes additional practice questions and examples, which further reinforce the understanding of the chapter.
Exam Preparation : By providing a structured approach to solving problems, these solutions help students prepare for exams more efficiently. They can practice different types of questions and familiarize themselves with the exam pattern.
Self-Assessment : Students can use these solutions to self-assess their understanding of the chapter. By comparing their answers with the provided solutions, they can identify areas where they need more practice or clarification.
Time Management : Efficiently solving problems with the help of these solutions can improve students' time management skills during exams or assessments.
Concept Reinforcement : The solutions not only solve problems but also reinforce the underlying mathematical concepts related to squares and square roots, ensuring a stronger foundation for future topics in mathematics.
ICSE Class 8 Maths Selina Solutions Chapter 3 FAQs
Which chapter is hard in maths class 8?
What is rational number class 8?
Is 70 percent good in class 8?
Is Class 8 very difficult?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
