ICSE Class 8 Maths Selina Solutions Chapter 4:
Cubes and Cube-Roots goes on several methods and techniques for locating cube roots, starting with the most fundamental ones. In order to practise the problems from the Class 8 Selina Maths textbook, students should read through the chapter and address any questions they may have. By clicking the provided link below to get the solutions PDF, they can double check their answers. A number's cube can be found by multiplying it by itself three times; for instance, 3.3.3=27 yields the cube of 3.
A few instances of flawless cubes include 1, 8, 27, 64, and so on. Conversely, the cube root is a unique value that yields the original number when cubed. For example, the cube root of 27 is 3, since 27 is the result of cubing 3.
ICSE Class 8 Maths Selina Solutions Chapter 4 Cubes and Cube Roots Overview
Chapter 4 of ICSE Class 8 Maths Selina Solutions focuses on cubes and cube roots, providing students with a thorough understanding of these fundamental mathematical concepts. The chapter begins by explaining what cubes and cube roots are, followed by detailed steps on how to calculate them.
Each concept is illustrated with examples and exercises that progressively increase in complexity, helping students grasp the nuances of cube numbers, cube roots, and their applications. By the end of the chapter, students not only gain proficiency in solving problems related to cubes and cube roots but also develop essential problem-solving skills applicable across various mathematical contexts.
ICSE Class 8 Maths Selina Solutions Chapter 4 PDF
Here we have provided ICSE Class 8 Maths Selina Solutions Chapter 4 for the ease of students so that they can just download the pdf and use it easily without the internet. These ICSE Class 8 Maths Selina Solutions Chapter 4 will help students understand the chapter better.
ICSE Class 8 Maths Selina Solutions Chapter 4 PDF
ICSE Class 8 Maths Selina Solutions Chapter 4
ICSE Class 8 Maths Selina Solutions Chapter 4 Exercise 1.
Here we have provided ICSE Class 8 Maths Selina Solutions Chapter 4 for the ease of students so that they can prepare better for their upcoming exams -
Find the cube of:
(i) 7
(ii) 11
(iii) 16
(iv) 23
(v) 31
(vi) 42
(vii) 54
Question 2
Find which of the following perfect cubes are:
(i) 243
(ii) 588
(iii) 1331
(iv) 24000
(v) 1728
(vi) 1938
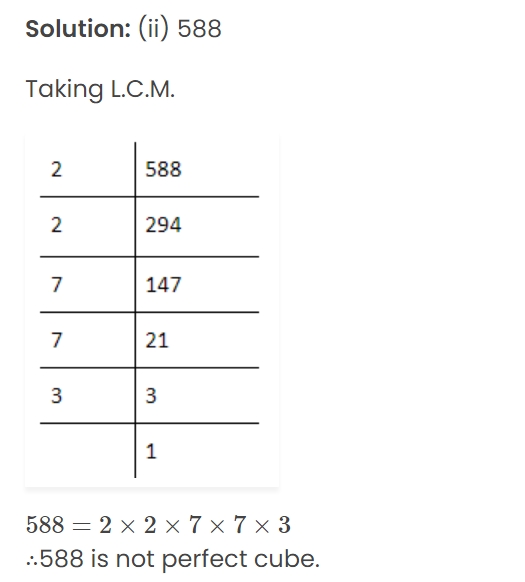
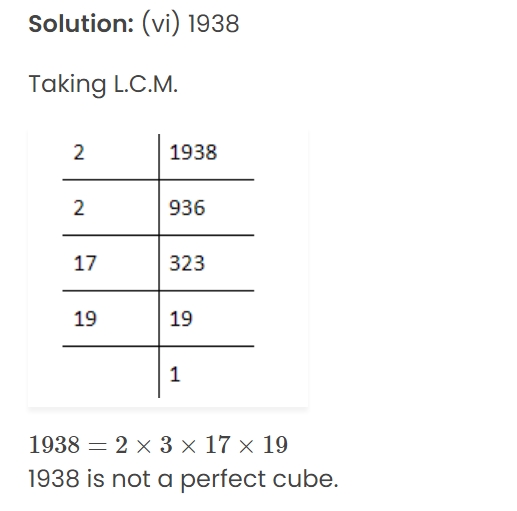
Question 3.
Find the cubes of:
(i) 2.1
(ii) 0.4
(iii) 1.6
(iv) 2.5
(v) 0.12
(vi) 0.02
Solution:
(i) 2.1
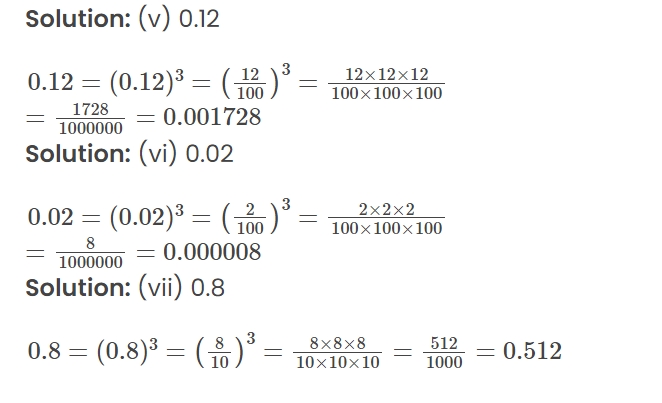
Question 4
Find the cubes of:
Question 5.
Find the cubes of:
(i) -3
(ii) -7
(iii) -12
(iv) -18
(v) -25
(vi) -30
(vii) -50
Solution:
(i) -3
Question 6.
Which of the following are cubes of?
(i) An even number
(ii) An odd number
216,729,3375,8000,125,343,4096 and 9261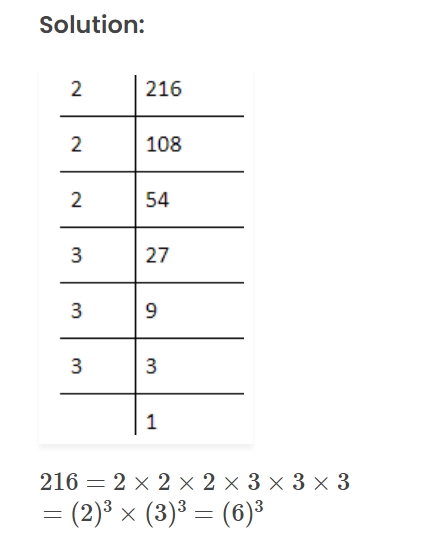
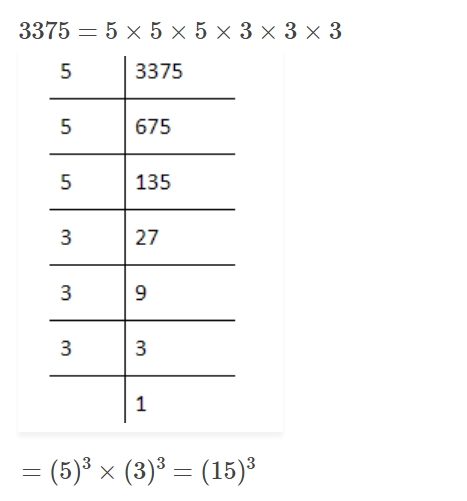(i) Cubes of an even number are 216, 8000, 4096.
(ii) Cubes of an odd number are 729, 3375, 125, 343, 9261
Question 7.
Find the least number by which 1323 must be multiplied so that the product is a perfect cube.
Solution:
The prime factor of 1323 are
Question 8.
Find the smallest number by which 8768 must be divided so that the quotient is a perfect cube.
Solution:
The prime factor of 8768 are
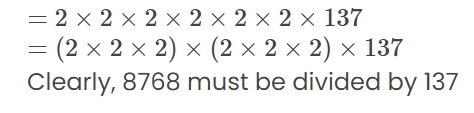
Question 9.
Find the smallest number by which 27783 be multiplied to get a perfect square number.
Solution:
Question 10.
With what least number must 8640 be divided so that the quotient is a perfect cube?
Solution:
The prime factors of 8640 are
Question 11.
Which is the smallest number that must be multiplied to 77175 to make it a perfect cube?
Solution:
The prime factors of 77175 are
ICSE Class 8 Maths Selina Solutions Chapter 4 Ex 4B
Question 1.
Find the cube-roots of:
(i)64
(ii) 343
(iii) 729
(iv) 1728
(v) 9261
(vi) 4096
(vii) 8000
(viii) 3375
Solution:
(i)64
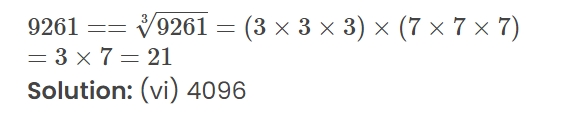
Benefits of ICSE Class 8 Maths Selina Solutions Chapter 4
The ICSE Class 8 Maths Selina Solutions for Chapter 4 on cubes and cube roots offer several benefits for students:
Clear Understanding of Concepts
: The solutions provided in the Selina textbook help students understand the fundamental concepts of cubes and cube roots clearly. This includes understanding what cubes and cube roots are, how they are calculated, and their applications in mathematics.
Step-by-Step Solutions
: The solutions are presented in a step-by-step manner, making it easier for students to follow and learn. This clarity helps in grasping the underlying mathematical principles involved in solving problems related to cubes and cube roots.
Practice Problems
: The Selina Solutions typically include a variety of practice problems covering different aspects of the chapter. These problems range in difficulty level, allowing students to gradually build their proficiency in applying cube and cube root concepts.
Application in Real-Life Scenarios
: Understanding cubes and cube roots is not just important for theoretical mathematics but also has practical applications in fields like geometry, engineering, and physics. The solutions provided often highlight these applications, thereby showing students the relevance of what they are learning.
Preparation for Exams
: ICSE examinations often include questions based on cubes and cube roots. By using the Selina Solutions, students can familiarize themselves with the types of questions asked in exams and gain confidence in tackling them effectively.
Enhanced Problem-Solving Skills
: Working through the solutions helps students develop critical thinking and problem-solving skills. They learn how to approach different types of problems related to cubes and cube roots, thereby improving their overall mathematical abilities.
Self-Assessment and Improvement
: The solutions also serve as a means for self-assessment. Students can compare their answers with the solutions provided, identify mistakes, and work on improving their understanding and accuracy.
