
Number System Formula: Numbers play a fundamental role in our daily activities, encompassing various aspects such as the hours of sleep we get, the laps we complete on a race track, and countless others. Within mathematics, numbers are classified into various categories including even and odd numbers, prime and composite numbers, decimals, fractions, rational and irrational numbers, natural numbers, integers, real numbers, rational numbers, irrational numbers, and whole numbers. This chapter aims to provide an overview of the diverse types of numbers and the associated concepts.
Also Check - Factorization FormulaWhat are Numbers?
Numbers serve as fundamental elements in the field of mathematics, serving various purposes like counting, measuring, arranging, and indexing. Different categories of numbers exist, each characterized by specific properties. These encompass natural numbers, whole numbers, rational and irrational numbers, integers, real numbers, complex numbers, even and odd numbers, and more. Through basic arithmetic operations, we can manipulate numbers and derive new values. In earlier times, tally marks were employed before the formal introduction of numerical symbols. This section will introduce the concept of numbers, delve into their various types, and explore their unique characteristics.
Also Check - Introduction to Graph FormulaIntroduction to Numbers
Numbers are the foundation of mathematics, and embracing them is essential for comprehending the subject. Numbers encompass a diverse array of categories, including ordinal numbers, consecutive numbers, odd and even numbers, natural numbers, whole numbers, integers, real numbers, rational numbers, irrational numbers, and complex numbers.
Within the realm of numbers, we delve into the intriguing domain of factors and multiples. This sphere encompasses prime numbers, composite numbers, co-prime numbers, and even introduces the concept of perfect numbers. Moreover, we explore concepts such as highest common factor (HCF), least common multiple (LCM), and the process of prime factorization.
Also Check - Line and Angles FormulaNumber Systems
The decimal number system is the prevailing numerical framework in use today. It employs the digits 0 through 9 to symbolize various quantities. Each digit within a given number possesses a distinct place value, contributing to the system's structure. This decimal system is the standard method for expressing both integers and non-integers. We rely on the decimal number system for the representation of numbers spanning from 1-digit figures to those with 10 digits, including 2-digit numbers, 3-digit numbers, 4-digit numbers, 5-digit numbers, 6-digit numbers, 7-digit numbers, 8-digit numbers, 9-digit numbers, and 10-digit numbers.
Also Check - Logarithm FormulaTypes of Numbers
The classification of numbers is based on their inherent properties. For instance, natural numbers encompass the counting sequence commencing from 1, while whole numbers encompass all non-negative integers, including 0. Prime numbers possess the distinctive trait of being divisible solely by 1 and the number itself, showcasing their uniqueness. Each type of number has its own set of defining characteristics, contributing to a diverse array of numerical categories. We will delve into the various types of numbers in greater detail in the subsequent sections.
Also Check - Ratio and Proportion FormulaDownload PDF Number System Formula
Numbers Chart
Various categories of numbers are employed in mathematical contexts, with each type defined by its distinct attributes. One way to classify these numbers is based on whether they fall within the realm of real numbers or extend into the realm of complex numbers. Real numbers encompass a wide spectrum of values, including rational, irrational, whole, and integers, which are often utilized in practical applications. Conversely, complex numbers encompass all numbers that lie outside the realm of real numbers, combining real and imaginary components. To gain a clearer understanding, let's refer to the real numbers chart provided below.

Cardinal Numbers and Ordinal Numbers
A cardinal number is used to represent the quantity or count of objects, like 1, 2, 3, and so on. On the other hand, an ordinal number is utilized to indicate the position or order of objects in a sequence, such as 1st, 2nd, 3rd, and so forth. While cardinal numbers specify how many items are present, ordinal numbers indicate the placement or sequence of those items.

Consecutive Numbers
Consecutive numbers are a sequence of numbers that occur in an uninterrupted order, progressing from the smallest to the largest number. Typically, each successive number in the sequence differs from the previous one by exactly 1.

Integers
Integers encompass both positive and negative whole numbers. These numbers are denoted by the symbol "Z" and do not include decimal or fractional components. A number line showcases integers, with negative integers on the left and positive ones on the right, with zero in the middle.
Z = { ...., -4, -3, -2, -1, 0 , 1, 2, 3, 4,....}
Natural Numbers and Whole Numbers
A natural number is a non-negative integer that is strictly greater than zero. It is denoted by the symbol "N". It's important to highlight that whole numbers do not possess any fractional or decimal component. They are symbolized by "W".

Even Numbers and Odd Numbers
Even numbers are those that can be evenly divided into two equal groups or pairs, and they are divisible by 2 without leaving a remainder. For instance, numbers like 2, 4, 6, 8, 10, and so forth fall into this category. In simpler terms, even numbers are whole numbers that can be divided by 2 with no remainder.
For illustration, consider the following diagram which demonstrates the divisibility of even numbers by 2:

[Diagram: Even numbers divided into equal groups]
On the other hand, odd numbers are whole numbers that cannot be divided into pairs evenly. These numbers cannot be evenly arranged in pairs, and notably, all whole numbers except for multiples of 2 are categorized as odd numbers.
To visualize this concept, take a look at the following diagram which highlights that odd numbers do not divide evenly by 2 and leave a remainder of 1 when divided by 2:

[Diagram: Odd numbers with remainder 1 when divided by 2]
Prime Numbers and Composite Numbers
A prime number is a number characterized by having precisely two factors: 1 and the number itself. Notable examples of prime numbers include 2, 5, 7, 11, and so forth. Essentially, any whole number greater than 1 that possesses precisely two factors, which are 1 and the number itself, is classified as a prime number.
To summarize, a prime number stands out due to its exclusive two factors: 1 and the number itself.
Conversely, a composite number possesses more than two factors, indicating that it can be divided by 1, itself, and at least one more integer. In essence, any number exceeding 1 that fails to meet the criteria of being a prime number is identified as a composite number. Composite numbers inherently possess a factor count exceeding 2. For instance, numbers like 6, 8, 9, 12, and others are considered composite numbers due to their multiple factors.
Also Check - Sequence and Series FormulaCo-prime Numbers
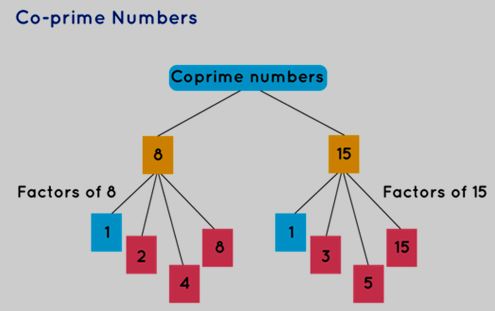
Co-prime numbers are pairs of numbers that share no common factors other than 1. In essence, when two integers possess only 1 as their common factor—resulting in their highest common factor (HCF) being 1—they are referred to as co-prime numbers. These numbers are also known as mutually prime numbers or relatively prime numbers. It is important to note that for two numbers to qualify as co-primes, they must form a pair.
In summary, co-prime numbers are characterized by having a sole common factor of 1, and they are often termed mutually prime or relatively prime numbers. It's worth emphasizing that the concept of co-prime numbers applies to pairs of integers.
Perfect Numbers
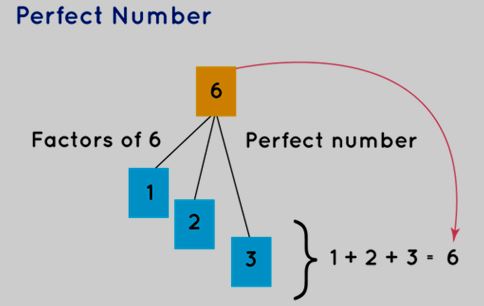
Perfect numbers are positive integers that satisfy the unique property of being equal to the sum of their divisors, excluding the number itself. In simpler terms, a perfect number is one where the sum of its proper divisors—factors other than the number itself—equals the number. The smallest perfect number, for instance, is 6, as it equals the sum of its proper divisors: 1, 2, and 3.
Fractions and Decimals
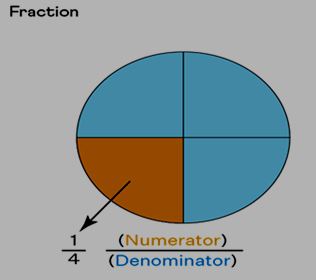
Fractions are mathematical expressions that represent a portion of a whole. They consist of two numerical components separated by a fraction bar. The upper number is known as the numerator, while the lower number is called the denominator.
Rational Numbers and Irrational Numbers
A rational number symbolized as Q, is expressed in the form p/q, where q is not equal to zero. Rational numbers encompass integers, fractions, decimals, whole numbers, and natural numbers. For instance, 1/2 and -4/5 are examples of rational numbers.
For a more comprehensive grasp of rational numbers, you can delve into related subjects such as the Decimal Representation of Rational Numbers and Operations on Rational Numbers.
On the other hand, irrational numbers are those that cannot be expressed as fractions with integers in the p/q format. The collection of irrational numbers is denoted as Q'. Examples of irrational numbers include √5 and √2.
Irrational numbers cannot be simplified into simple fractions. Their decimal expansion doesn't terminate or repeat in a pattern. Further exploration into irrational numbers can involve topics like the Square Root of Two is Irrational, Decimal Representation of Irrational Numbers, The exactness of Decimal Representation, Rationalize the Denominator, Surds, and Conjugates and Rationalization.

Complex Numbers
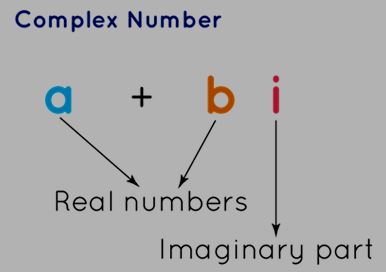
A complex number is a numerical entity represented in the form (a + bi), where 'a' and 'b' are real numbers, and 'i' is a solution of the equation x 2 = -1. Since there is no real number that satisfies this equation, 'i' is termed an imaginary number. Complex numbers consist of a real component and an imaginary component. Now, are these complex numbers as intricate as they sound? Let's delve into their intricacies to unravel the truth.
In this segment, we will explore various facets of complex numbers, including their geometric interpretation as points in the plane, the relationship between a complex number and its position in the plane, the concept of the imaginary unit 'i', the concepts of magnitude and argument, the rules for powers of 'i', performing addition and subtraction operations on complex numbers, multiplication of complex numbers, understanding the conjugate of a complex number, division of complex numbers, as well as comprehending the significance of |z1-z2| through addition and subtraction operations and interpretation. Through this comprehensive exploration, we aim to demystify the complexity associated with complex numbers and provide a clearer understanding of their properties and applications.
Factors and Multiples
Factors and multiples are fundamental concepts often studied in tandem. Factors refer to numbers that divide a given number evenly, leaving no remainder. On the other hand, multiples are numbers obtained by multiplying another number by various factors to yield specific results.
Also Check - Squares and Square Roots FormulaHighest Common Factor (HCF)
The Highest Common Factor (HCF) or Greatest Common Factor (GCF) of two numbers is the largest whole number that can evenly divide both numbers without leaving a remainder.
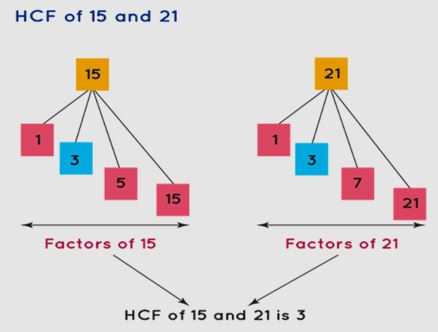
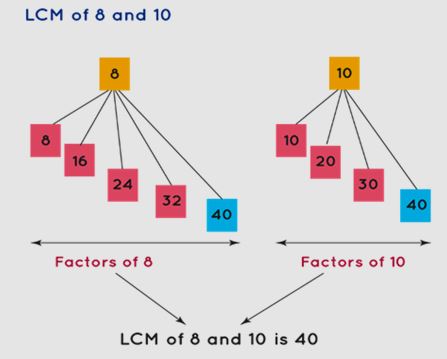
Least Common Multiple (LCM)
When dealing with two numbers, each number will have its respective set of multiples. Among these multiples, there are some that are common to both numbers. The smallest of these common multiples is referred to as the Least Common Multiple (LCM) of the two numbers.
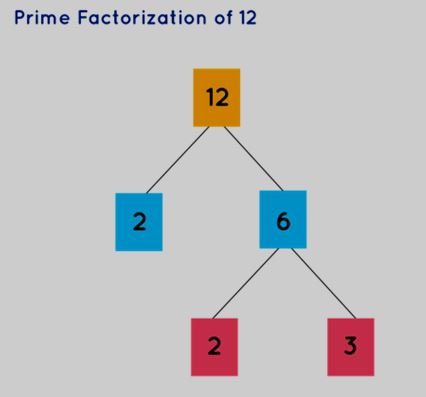
Prime Factorization
Prime factorization provides a method to represent any number as a multiplication of its prime factors. It involves expressing a number as a product of its prime factors. To perform prime factorization, we decompose a number into its constituent prime factors.
Number System Formula FAQs
Explain the term Number System.
What is a Prime Number?
What is a Perfect Number?
Define the term Complex Number.










