
Odd Number Formula: Odd numbers are those that cannot be paired up evenly. In simpler terms, any number that isn't a multiple of 2 falls into the category of odd numbers.
Odd numbers are integers that cannot be evenly divided by 2, resulting in a remainder of 1 when divided by 2. In other words, odd numbers are those that are not multiples of 2. The sequence of odd numbers starts with 1 and then follows an increment of 2 (3, 5, 7, 9, and so on).
Also Check - Volume of a Hemisphere FormulaWhat are Odd Numbers?
Odd numbers are numerical values that resist being divided into two equal parts. To put it differently, odd numbers are positive whole numbers that don't neatly fit into pairs.
Meaning of Odd Numbers
Let's grasp the concept of odd numbers through an illustrative example. Consider numbers like 1, 3, 5, 7, and so forth. These numbers resist pairing up. To better visualize this, let's use an analogy involving shoes and cherries. Examine the diagram below to gain insight into how these numbers can or cannot be paired. We have groupings of shoes in quantities of 1, 3, 5, and 7. In contrast, we have cherries arranged in twos – 2, 4, 6, and 8.
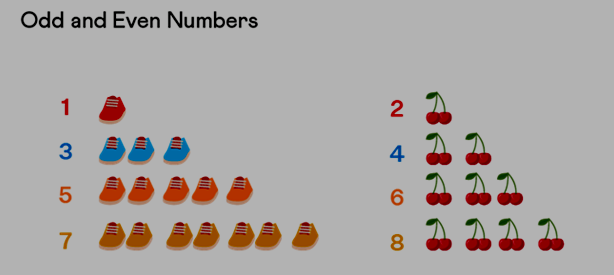
Odd numbers
It's important to note that shoes, representing odd numbers, lack complete pairs. One shoe always remains unpaired. On the flip side, cherries, which represent even numbers, are divisible into two equal parts, forming complete pairs. For instance, 4 cherries can be split into 2 pairs of 2, and 8 cherries can be divided into 4 pairs of 2, and so on.
Hence, we can conclude that odd numbers do not lend themselves to pairing.
Also Check - Comparing Quantities FormulaList of Odd Numbers
Let's examine the roster of odd numbers spanning from 1 to 200 and put into practice the insights we've acquired thus far. It's important to emphasize that none of the figures listed below are divisible by 2. Additionally, it's worth highlighting that among the initial 200 numbers, merely 100 of them qualify as odd numbers. Take a moment to peruse the compilation of odd numbers within the range of 1 to 200 provided below:
In this sequence, we can observe that each number remains unpaired, substantiating their oddness, as they cannot be evenly divided by 2.
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 |
| 21 | 23 | 25 | 27 | 29 | 31 | 33 | 35 | 37 | 39 |
| 41 | 43 | 45 | 47 | 49 | 51 | 53 | 55 | 57 | 59 |
| 61 | 63 | 65 | 67 | 69 | 71 | 73 | 75 | 77 | 79 |
| 81 | 83 | 85 | 87 | 89 | 91 | 93 | 95 | 97 | 99 |
| 101 | 103 | 105 | 107 | 109 | 111 | 113 | 115 | 117 | 119 |
| 121 | 123 | 125 | 127 | 129 | 131 | 133 | 135 | 137 | 139 |
| 141 | 143 | 145 | 147 | 149 | 151 | 153 | 155 | 157 | 159 |
| 161 | 163 | 165 | 167 | 169 | 171 | 173 | 175 | 177 | 179 |
| 181 | 183 | 185 | 187 | 189 | 191 | 193 | 195 | 197 | 199 |
The concept we've assimilated previously finds practical application in this tabulated data, streamlining our comprehension, wouldn't you agree? Take a moment to peruse the provided table and endeavor to identify commonalities among these enumerated values.
Were you able to discern a consistent pattern within the list of odd numbers above?
Remarkably, within the odd numbers list, the unit digit consistently retains the values 1, 3, 5, 7, or 9.
Also Check - Introduction to Graph FormulaProperties of Odd Numbers
The subsequent points outline the distinctive properties of odd numbers. Each of these properties can be elucidated in a more comprehensive manner as elaborated below.
Addition of Odd Numbers: When two odd numbers are added, the outcome is invariably an even number. In other words, the summation of two odd numbers consistently yields an even number. For instance, the combination of 3 (an odd number) and 5 (also an odd number) yields 8 (an even number).
Subtraction of Odd Numbers: Whenever two odd numbers are subtracted from each other, the result is consistently an even number. To put it differently, the difference between two odd numbers is always an even number. As an illustration, subtracting 1 (an odd number) from 7 (another odd number) results in 6 (an even number).
Multiplication of Odd Numbers: The product of two odd numbers is perpetually an odd number. When two odd numbers are multiplied together, the outcome is consistently an odd number. For instance, multiplying 3 (an odd number) by 7 (also an odd number) gives 21 (an odd number).
Division of Odd Numbers: Dividing one odd number by another odd number invariably yields an odd number. In other words, the quotient obtained from the division of two odd numbers is always an odd number. For example, dividing 33 (an odd number) by 11 (another odd number) results in 3 (an odd number).
These properties underscore the consistent behavior of odd numbers in various mathematical operations, providing insights into their distinct characteristics and behavior.
This table succinctly presents the properties of odd numbers and their outcomes in various mathematical operations.
| Arithmetic Operation | Result |
|---|---|
| Odd number + Odd number | Even number |
| Odd number - Odd number | Even number |
| Odd number × Odd number | Odd number |
| Odd number ÷ Odd number | Odd number |
Types of Odd Numbers
Odd numbers encompass all the numerical values that aren't divisible by 2, creating a vast collection of numbers. This diversity prompts the emergence of various categories of odd numbers, based on factors, inter-number intervals, positions on the number line, and more.
Consecutive Odd Numbers:
Consecutive odd numbers are those odd integers that appear in sequential order. For instance, if 'n' represents an odd number, then the numbers 'n' and 'n + 2' fall into the category of consecutive odd numbers. These pairs exhibit a consistent difference of 2 between them and are characterized by their consecutive arrangement. For instance, pairs like 3 and 5, 11 and 13, 25 and 27, 37 and 39, 49 and 51, adhere to this pattern.
Composite Odd Numbers:
Composite odd numbers are odd integers that are not classified as prime numbers. These particular odd numbers result from the multiplication of two smaller positive odd integers. Within the range of 1 to 100, the composite odd numbers include 9, 15, 21, 25, 27, 33, 35, 39, 45, 49, 51, 55, 57, 63, 65, 69, 75, 77, 81, 85, 87, 91, 93, 95, and 99. These numbers are distinct due to their composite nature, formed by the combination of smaller odd factors.
The Smallest Odd Number:
The tiniest odd number is 1, as odd numbers commence from 1 and extend in sequence as follows: 1, 3, 5, 7, 9, 11, and so forth.
First 10 Odd Numbers:
The initial ten odd numbers encompass 1, 3, 5, 7, 9, 11, 13, 15, 17, and 19.
The Smallest Odd Composite Number:
The most compact odd composite number is 9. Although the exploration for the smallest composite number commences with 4, it is an even number. Subsequent numbers such as 6 and 8 also exhibit even characteristics. This sequence culminates with 9, an odd number, thus marking the onset of the smallest odd composite number.
Odd Prime Numbers:
Odd prime numbers denote prime numbers that are also odd. Interestingly, all prime numbers, excluding 2, are odd numbers.
Odd Natural Numbers:
Odd natural numbers refer to those natural numbers which are odd. As a fundamental principle, natural numbers encompass positive integers beginning with 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, extending infinitely. When sifting out the odd numbers from this sequence, we yield 1, 3, 5, 7, 9, and so forth.
Useful Insights on Odd Numbers
Here are a few practical insights and techniques pertaining to odd numbers that can aid in grasping concepts more rapidly:
- The sum of two odd numbers always results in an even number.
- A quick differentiation between odd and even numbers involves dividing by 2.
- If division yields a remainder of 1, the number is odd, indicating it cannot be divided evenly into two parts.
- If division yields a remainder of 0, the number is even, signifying its divisibility into two equal parts.
- Odd numbers consistently have 1, 3, 5, 7, or 9 as their units place digit. Conversely, even numbers feature 0, 2, 4, 6, or 8 in their unit place.
Odd Numbers Formula Example
Example 1: Determine the nature of 135 as an odd or even number.
Solution:
We can ascertain this using either of the provided methods:
Method 1: Examine the digit at the unit place. The unit's place of 135 is occupied by the digit 5, an odd number. Thus, it follows that the given number, 135, is odd.
Method 2: It's necessary to explore the divisibility of 135 by 2. Upon dividing 135 by 2, the remainder obtained is 1. This demonstrates that 135 is an odd number.
Consequently, we can definitively conclude that 135 belongs to the category of odd numbers.
Example 2: Addressing Questions Related to Odd Numbers:
a.) 1 is classified as an odd number.
b.) The most compact 4-digit odd number is 1001.
c.) The smallest odd composite number is 9.
d.) The aggregate of any two odd numbers invariably results in an even number.
e.) No, 2 is not categorized as an odd number; it is an even number.
Example 3: Determining True or False Statements Regarding Odd Numbers:
a.) True, the cumulative sum of two odd numbers consistently yields an even number.
b.) False, the smallest odd number is 1.
c.) False, not all prime numbers are odd; for instance, 2 is a prime number and is even. Generally, prime numbers, except for 2, are odd.
d.) True, indeed, 9 is an odd number.
Odd Number Formula FAQs
What are Odd Numbers?
What is the difference between Odd numbers and Even numbers?
Is 0 classified as an even or odd number?
Define the GCD of two consecutive odd numbers.










