Three Dimensional Geometry coordinates serve as essential markers on our planet, allowing us to easily pinpoint locations on the world map. The Earth's coordinate system comprises imaginary lines known as latitudes and longitudes. Starting points for this system are the zero degrees 'Greenwich Longitude' and the zero degrees 'Equator Latitude.' In a similar manner, when locating a point on a plane or a piece of paper, we utilize coordinate axes consisting of the horizontal x-axis and the vertical y-axis.
Coordinate geometry is the field that examines geometric shapes by plotting them on the coordinate axes. Various shapes, including straight lines, curves, circles, ellipses, hyperbolas, and polygons, can be accurately drawn and scaled on the coordinate axes. Furthermore, coordinate geometry facilitates algebraic calculations and the exploration of geometric figure properties through the use of the coordinate system.
3D Geometry
Three-dimensional (3D) Geometry serves as a method for representing points, lines, or planes in relation to the x-axis, y-axis, and z-axis. In this branch of mathematics, the principles and concepts closely resemble those of two-dimensional coordinate geometry.
Explore further into the realm of 3D geometry, including the representation of points, lines, and planes, through illustrative examples and frequently asked questions (FAQs).
What Is 3D Geometry?
Three-dimensional geometry is a valuable tool for representing lines or planes within a three-dimensional space, utilizing the x-axis, y-axis, and z-axis. Each point in three-dimensional geometry is defined by three coordinates, typically denoted as (x, y, z).
The three-dimensional Cartesian coordinate system comprises three mutually perpendicular axes: the x-axis, the y-axis, and the z-axis. These axes share the same units of length across all three dimensions. Similar to the two-dimensional coordinate system, the point where these three axes intersect is known as the origin (O), and they divide the space into eight octants. Each point in 3D Geometry can be represented by coordinates in the form of (x, y, z).
Furthermore, the coordinates of points in the eight octants are as follows:
(+x, +y, +z)
(-x, +y, +z)
(+x, +y, -z)
(-x, +y, -z)
(+x, -y, +z)
(-x, -y, +z)
(+x, -y, -z)
(-x, -y, -z)
In a Cartesian coordinate system, notation is used to present points for ease of understanding and calculation. Points are enclosed in parentheses and separated by commas. For instance, an example of a point in a three-dimensional frame is (2, 5, 4). The origin is symbolized as 'O,' and the coordinates of a point are represented as (x, y, z). Typically, the last letters of the alphabetical series are employed, or the initial letters of words are used to denote the coordinates of a point.
Understanding the following three essential terms is crucial when dealing with coordinates:
- Abscissa: This refers to the x-value in the point (x, y, z) and represents the distance of the point along the x-axis from the origin.
- Ordinate: The y-value in the point (x, y, z) indicates the perpendicular distance of the point from the x-axis while remaining parallel to the y-axis.
- Applicate: In a three-dimensional context (x, y, z), the z-coordinate of the point is referred to as the applicate. It signifies the position along the z-axis.
Also Check - Inverse Trigonometric Functions
Three Dimensional Geometry - Important Concepts
Three-dimensional geometry employs three coordinates to represent a point and encompasses several important concepts that facilitate understanding and analysis. Some crucial concepts within three-dimensional geometry include direction ratios, direction cosines, the distance formula, midpoint formula, and the section formula. Here are further details about these important concepts:
Direction Ratios:
Point A with coordinates (a, b, c) can be represented as a vector Direction ratios (a, b, c) define the vector's orientation in relation to the x-axis, y-axis, and z-axis. These ratios play a fundamental role in various geometric calculations and are used to derive direction cosines.
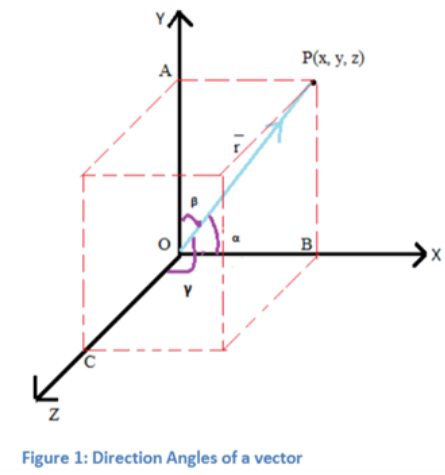
Direction Cosines:
Direction cosines establish the relationship between a vector or a line in three-dimensional space and each of the three axes (x, y, z).
Direction cosines are the cosines of the angles formed between the line and the x-axis, y-axis, and z-axis respectively.
If the angles formed by the line with the three axes are α, β, and γ, then the direction cosines are represented as Cosα, Cosβ, and Cosγ.
the direction cosines are calculated as follows:
Direction cosines are often denoted as l, m, n, and it can be proven that
These concepts are fundamental in three-dimensional geometry, enabling precise characterization of vectors and lines in space and aiding in various geometric calculations and analyses.
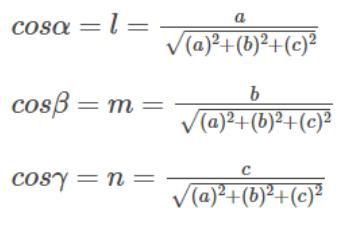
Download PDF 3D Geometry Distance Formula
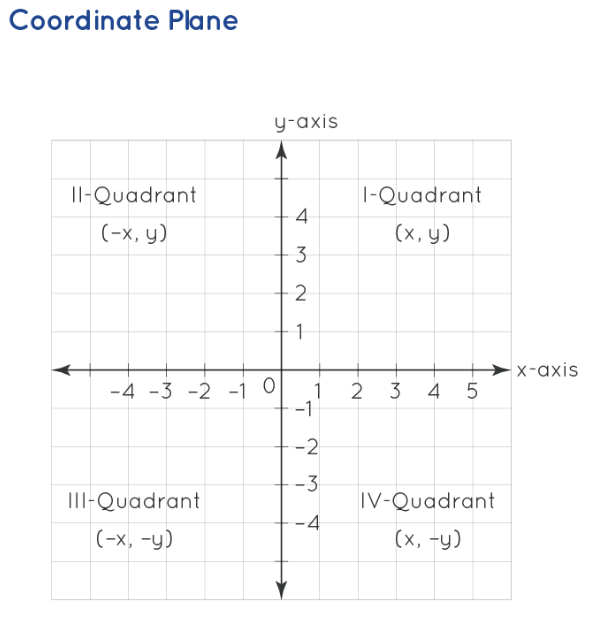
The Coordinate Plane
A Cartesian plane divides the plane's space into two dimensions, enabling the easy identification of points. This plane is also known as the coordinate plane and features two axes: the horizontal x-axis and the vertical y-axis. These axes partition the plane into four quadrants, with the intersection point being the origin (0, 0). Any point on the coordinate plane is designated by a pair of coordinates (x, y), where the x-coordinate represents the point's position along the x-axis, and the y-coordinate represents its position along the y-axis.
Key characteristics of points within the four quadrants are as follows:
- The origin O, positioned at the intersection of the x-axis and y-axis, has coordinates (0, 0).
- To the right of the origin O, the x-axis is positive, and to the left, it is negative. Similarly, above the origin O, the y-axis is positive, while below it is negative.
- A point in the first quadrant (x, y) possesses positive values for both x and y and is situated relative to the positive x-axis and y-axis.
- In the second quadrant, a point (-x, y) is positioned with respect to the negative x-axis and positive y-axis.
- The third quadrant features a point (-x, -y), plotted relative to the negative x-axis and negative y-axis.
- The fourth quadrant hosts a point (x, -y), situated relative to the positive x-axis and negative y-axis.
Key concepts and topics in 3D geometry include:
Coordinates: Points in three-dimensional space are represented using Cartesian coordinates, typically denoted as (x, y, z), where x, y, and z represent the distances along the x-axis, y-axis, and z-axis, respectively. These coordinates are used to pinpoint the location of objects in 3D space.
Vectors and Vector Operations : Vectors are quantities that have both magnitude and direction. In 3D geometry, vectors are employed to describe translations, displacements, and directions. Vector operations, such as addition, subtraction, dot product, and cross product, are essential tools for solving problems in 3D geometry.
Lines and Planes: The study of lines and planes in 3D space involves understanding their equations, intersections, and orientations. Lines can be specified using vector equations or parametric equations, while planes can be described in various forms, including point-normal form and intercept form.
Distance and Midpoint: Calculating distances between points and determining the midpoint of line segments are common tasks in 3D geometry. Formulas for these calculations are essential tools for solving geometric problems.
Equations of Surfaces: Different types of surfaces, such as spheres, cylinders, cones, and planes, are analyzed in 3D geometry. Understanding their equations and properties is crucial for various applications.
Solid Geometry: Solid geometry deals with the study of three-dimensional objects, or solids, including prisms, pyramids, cubes, spheres, and more.
Calculating volumes, surface areas, and other properties of solids is a fundamental aspect of this branch of geometry.
3D geometry has wide-ranging applications in various fields, including engineering, physics, computer graphics, architecture, and more. It plays a crucial role in modeling and analyzing three-dimensional objects and structures in the real world.
3D Geometry Formulas
Coordinate geometry formulas play a pivotal role in demonstrating the properties of lines and shapes represented on coordinate axes. These formulas encompass the distance formula, slope formula, midpoint formula, section formula, and line equation. Each formula serves a distinct purpose in coordinate geometry:
Also Check – Basics of Geometry Formula
3D Geometry Distance Formula
Distance Formula:
This formula computes the distance between two points (x1, y1) and (x2, y2) as the square root of the sum of squared differences in their x and y coordinates.
Distance (D) = √(x2−x1) 2 +(y2−y1) 2
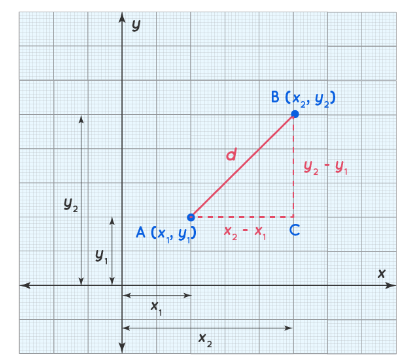
from the above figure:
By the Pythagoras’ theorem,
AB 2 = AC 2 + BC 2
d 2 = (x2 – x1) 2 + (y2 – y1) 2
Taking the square root on both sides,
d = √[(x2 – x1) 2 + (y2 – y1) 2 ]
This is called the distance between two points formula.
3D Geometry Slope Formula
Slope Formula :
The slope of a line can be calculated using the angle it forms with the positive x-axis or by selecting two points on the line.
Slope (m) = Tanθ = (y2 - y1) / (x2 - x1)
Also Check – Logarithm Formula
Finding Slope from a Graph
The slope of a line has only one value. So, the slopes found by Methods 1 and 2 will be equal. In addition to that, let's say we are given the equation of a straight line. The general equation can be given as,
y = mx + b
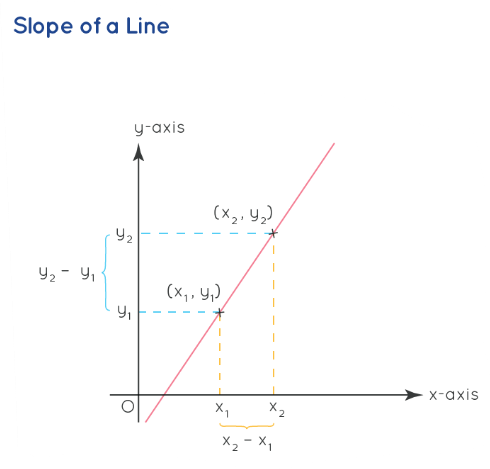
The value of the slope is given as m; hence the value of m gives the slope of any straight line.
The below-given steps can be followed to find the slope of a line such that the coordinates of two points lying on the line are: (2, 4), (1, 2)
- Step 1: Note the coordinates of the two points lying on the line, (x 2 , y 2 ), (x 1 , y 1 ). Here the coordinates are given as (2, 4), (1, 2).
- Step 2: Apply the slope of line formula, m = (y 2 - y 1 )/(x 2 - x 1 ) = (4 - 2)/(2 - 1) = 2.
- Step 3: Therefore, the slope of the given line = 2.

3D Geometry Midpoint Formula
Midpoint Formula:
This formula determines the midpoint of a line joining two points (x1, y1) and (x2, y2). The midpoint's coordinates are the averages of the x and y coordinates of the given points.
Given two points A (x 1 , y 1 ) and B (x 2 , y 2 ), the midpoint between A and B is given by,
M(x 3 , y 3 ) = ((x 1 + x 2 )/2, (y 1 + y 2 )/2)
where, M is the midpoint between A and B, and (x 3 , y 3 ) are its coordinates.
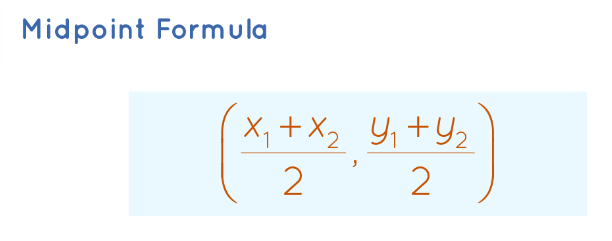
Midpoint (x, y) = ((x1 + x2) / 2, (y1 + y2) / 2)
Also Check – Introduction to Graph Formula
3D Geometry Section Formula
Section Formula:
The section formula identifies the coordinates of a point that divides the line segment between two points (x1, y1) and (x2, y2) in a given ratio m:n.
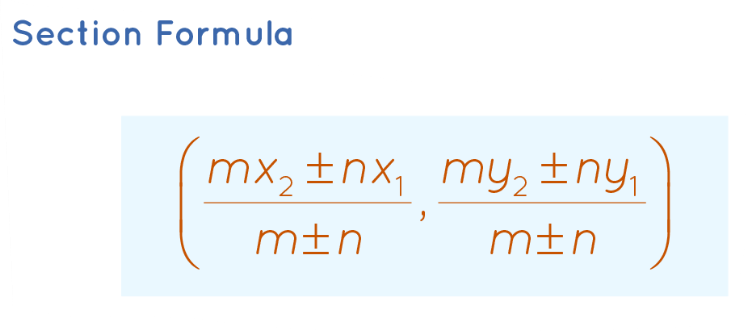
Point (x, y) = ((mx2 + nx1) / (m + n), (my2 + ny1) / (m + n))
3D Geometry Centroid Formula
Centroid Formula:
The centroid of a triangle formed by vertices A (x1, y1), B (x2, y2), and C (x3, y3) can be found using the formula:
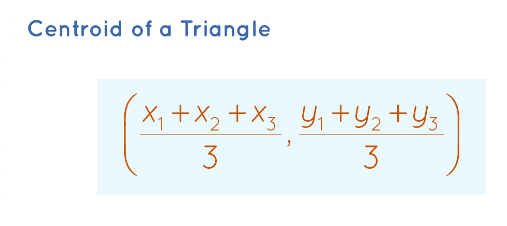
Centroid (x, y) = ((x1 + x2 + x3) / 3, (y1 + y2 + y3) / 3)
3D Geometry Representation of A Point, Line, Plane
Three-dimensional geometry serves as a tool for depicting points, lines, and planes in space. Let's explore the different methods of representing points, lines, and planes in three-dimensional geometry.
Representation of a Point in 3D Geometry:
In three-dimensional geometry, a point can be represented in either cartesian form or vector form. Here are the two forms of point representation in 3D geometry:
Cartesian Form: The cartesian form of representing a point in three-dimensional geometry involves using three coordinates in relation to the x-axis, y-axis, and z-axis. These coordinates for any point in 3D geometry are denoted as (x, y, z). Specifically:
- The x-value of the point is referred to as the abscissa.
- The y-value of the point is known as the ordinate.
- The z-value of the point is called the applicate.
This cartesian representation provides a precise way to pinpoint the location of a point within three-dimensional space.
Representation of A Line in 3D Geometry
The equation of a line within a three-dimensional Cartesian system can be determined using two distinct methods. These two methods for finding the equation of a line are as follows:
Equation of a Line Passing Through a Point 'a' and Parallel to a Given Vector 'b':
In this method, the equation of a line is expressed as: r = a + λb.
Here, 'r' represents the position vector of any point on the line.
'a' denotes a specific point through which the line passes.
'λ' is a parameter that allows for the variation along the line.
'b' signifies a given vector that determines the line's direction.
This equation describes a line passing through point 'a' and being parallel to vector 'b.'
Equation of a Line Passing Through Two Given Points, 'a' and 'b':
In this method, the equation of a line is presented as: r = a + λ(b - a).
Once again, 'r' signifies the position vector of any point on the line.
'a' and 'b' represent two specific points through which the line passes.
'λ' remains a parameter allowing for adjustments along the line.
This equation characterizes a line passing through points 'a' and 'b' and allows for the determination of all points along the line's path.
These methods provide a mathematical framework for defining lines within three-dimensional space based on different scenarios, whether it involves a point and a vector or two distinct points.
Also Check – Congruence of Triangles Formula
Representation of A Plane in 3D Geometry
The equation of a plane within a Cartesian coordinate system can be determined using various methods, depending on the available information about the plane. Here are four different expressions for the equation of a plane:
Normal Form: The equation of a plane situated at a perpendicular distance 'd' from the origin and possessing a unit normal vector n
![]()
Perpendicular to a Given Line and Through a Point: When defining a plane that is perpendicular to a specified vector N and passing through the point a
![]()
Through Three Non-Collinear Points: To establish the equation of a plane passing through three collinear points a, b, and c, the equation takes the form
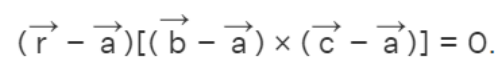
Intersection of Two Planes: When determining the equation of a plane that passes through the intersection of two planes img
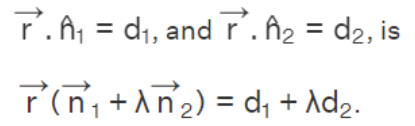
These expressions provide versatile methods for defining planes within a Cartesian coordinate system based on different scenarios and input values related to the plane's orientation and position.
Determining the Equation of a Line in Coordinate Geometry
The equation of a line represents all points on the line through a linear equation. The standard form is ax + by + c = 0, where a, b, and c are constants. Several methods, including the slope-intercept form (y = mx + c), are used to find the equation. Other forms, such as the point-slope form, two-point form, intercept form, and normal form, provide additional perspectives on line equations.
Coordinate geometry offers a powerful toolset for understanding and analyzing geometric shapes within a coordinate system. By utilizing these concepts and formulas, mathematicians and researchers can explore the intricate relationships between points, lines, and figures on a two-dimensional plane
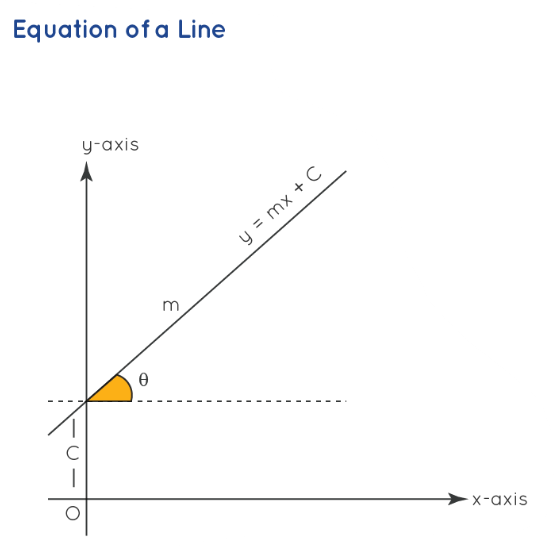
Points to Remember About Aartesian Coordinates
- The slope of the x-axis holds a value of 0, while the slope of the y-axis is considered infinite (∞).
- The x-axis is represented by the equation y = 0, and the y-axis is described by the equation x = 0.
- A point situated on the x-axis takes the form (a, 0), whereas a point located on the y-axis is represented as (0, b).
- The equation of a line in slope-intercept form is y = mx + c.
- In the coordinate plane, two lines that are parallel possess equal slopes.
- Furthermore, in the coordinate plane, when considering two perpendicular lines, the product of their slopes is equivalent to -1. Coordinate Geometry FAQ
Three Dimensional Geometry Formula FAQs
Q1. Define the term 3D geometry.
Q2. What is the meaning of the coordinate plane?
Q3. What is the importance of Coordinate Geometry?
Q4. Explain the term Abscissa and Ordinates in Coordinate Geometry.