NCERT Solutions for Class 12 Maths Chapter 9 Exercise 9.1 (Differential Equations)
NCERT Solutions for Class 12 Maths Chapter 9 Exercise 9.1 contains all the questions with detailed solutions. Students are advised to solve these questions for better understanding of the concepts in exercise 9.1.
Krati Saraswat22 Feb, 2024
Share
NCERT Solutions for Class 12 Maths Chapter 9 Exercise 9.1 (Differential Equations)
NCERT Solutions for Class 12 Maths Chapter 9 Exercise 9.1 Differential Equations is prepared by the academic team of Physics Wallah. We have prepared NCERT Solutions for all exercise of Chapter 9. Given below is step by step solutions to all questions given in the NCERT Solutions for Class 12 Maths Chapter 9 Exercise 9.1 Differential Equations.
NCERT Solutions for Class 12 Maths Chapter 9 Miscellaneous Exercise
NCERT Solutions for Class 12 Maths Chapter 9 Exercise 9.1 Overview
NCERT Solutions for Class 12 Maths Chapter 9 Exercise 9.1 cover several important topics. It is highly recommended for students to review each topic thoroughly in order to gain a comprehensive understanding of the concepts taught in the chapter and make optimal use of the provided solutions. These solutions are the result of dedicated efforts by the Physics Wallah teachers aimed at assisting students in grasping the concepts covered in this chapter. By going through and practicing these solutions, the objective is for students to achieve excellent results in their exams effortlessly.NCERT Solutions for Class 12 Maths Chapter 9 Exercise 9.1
Solve The Following Questions of NCERT Solutions for Class 12 Maths Chapter 9 Exercise 9.1
Determine order and degree (if defined) of differential equations given in Questions 1 to 10: Question 1.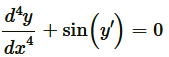
Solution :
Given:
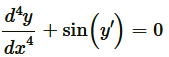
The highest order derivative present in the differential equation is y'''' and its order is 4.
The given differential equation is not a polynomial equation in its derivatives. Hence, its degree is not defined.
NCERT Solutions for Class 12 Maths Chapter 9 Exercise 9.2
Question 2. y' + 5y = 0 Solution : The given differential equation is: y' + 5y = 0 The highest order derivative present in the differential equation is y'. Therefore, its order is one. It is a polynomial equation in y'. The highest power raised to y'is 1. Hence, its degree is one.NCERT Solutions for Class 12 Maths Chapter 9 Exercise 9.3
Question 3.
Solution :
Given:
The highest order derivative present in the given differential equation is d
2
s/dt
2
Therefore, its order is two.
It is a polynomial equation in d
2
s/dt
2
and ds/dt. The power raised to d
2
s/dt
2
is 1.
Hence, its degree is one.
NCERT Solutions for Class 12 Maths Chapter 9 Exercise 9.4
Question 4.
Solution :
Given:
The highest order derivative present in the given differential equation is d
2
y/dx
2
Therefore, its order is 2.
The given differential equation is not a polynomial equation in its derivatives. Hence, its degree is not defined.
NCERT Solutions for Class 12 Maths Chapter 9 Exercise 9.5
Question 5.
Solution :
Given:
The highest order derivative present in the differential equation is d
2
y/dx
2
and its order is 2.
The given differential equation is a polynomial equation in derivatives and the highest power raised to highest order d
2
y/dx
2
is one, so its degree is 1.
Hence, order is 2 and degree is 1.
NCERT Solutions for Class 12 Maths Chapter 9 Exercise 9.6
Question 6.
Solution :
Given:
The highest order derivative present in the differential equation is y'''. Therefore, its order is three.
The given differential equation is a polynomial equation in y''', y'', and y'.
The highest power raised to y''' is 2. Hence, its degree is 2.
Question
7.
y''' + 2y'' + y' = 0
Solution :
Given: y''' + 2y'' + y' = 0
The highest order derivative present in the differential equation is y'''. Therefore, its order is three.
It is a polynomial equation in y''', y'' and y'. The highest power raised to y'''is 1. Hence, its degree is 1.
Question
8.
y′ + y = e
x
Solution :
Given: y′ + y = e
x
⇒ y′ + y - e
x
= 0
The highest order derivative present in the differential equation is y'. Therefore, its order is one.
The given differential equation is a polynomial equation in y' and the highest power raised to y' is one. Hence, its degree is one.
Question
9.
y'′ + (y')
2
+ 2y = 0
Solution :
Given: y'′ + (y')
2
+ 2y = 0
The highest order derivative present in the differential equation is y''. Therefore, its order is two.
The given differential equation is a polynomial equation in y''and y' and the highest power raised to y'' is one.
Hence, its degree is one.
Question
10.
y'′ + 2y' + sin y = 0
Solution :
Given: y'′ + 2y' + sin y = 0
The highest order derivative present in the differential equation is y''. Therefore, its order is two.
This is a polynomial equation in y''. and y'.and the highest power raised to y''. is one. Hence, its degree is one.
Question
11. The degree of the differential equation is:
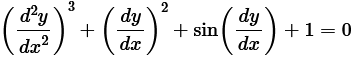(A) 3
(B) 2
(C) 1
(D) Not defined
Solution :
Given:
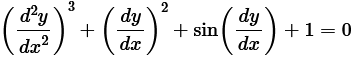……….(i)
The given differential equation is not a polynomial equation in its derivatives. Therefore, its degree is not defined.
Hence, the correct answer is D.
Hence, option (D) is correct.
Question
12. The order of the differential equation is:
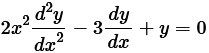(A) 2
(B) 1
(C) 0
(D) Not defined
Solution :
Given:
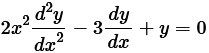The highest order derivative present in the differential equation is d
2
y/dx2 and its order is 2.
Therefore, option (A) is correct.
NCERT Solutions For Class 12 Maths Chapter 9 Exercise 9.1 FAQs
How many exercises are there in differential equations?
There are a total of 113 questions in the NCERT Solutions Class 12 Maths Chapter 9 Differential Equations that are divided among 7 exercises.
What is the concept of differential equation class 12?
In Mathematics, a differential equation is an equation that contains one or more functions with its derivatives.
Is differential equations easy class 12?
In Mathematics, a differential equation is an equation that contains one or more functions with its derivatives. The derivatives of the function define the rate of change of a function at a point. It is mainly used in fields such as physics, engineering, biology and so on.
What classes use differential equations?
The study of differential equations is a wide field in pure and applied mathematics, physics, and engineering.
Who is the father of differential equations?
Isaac Newton is the father of differential equations.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.