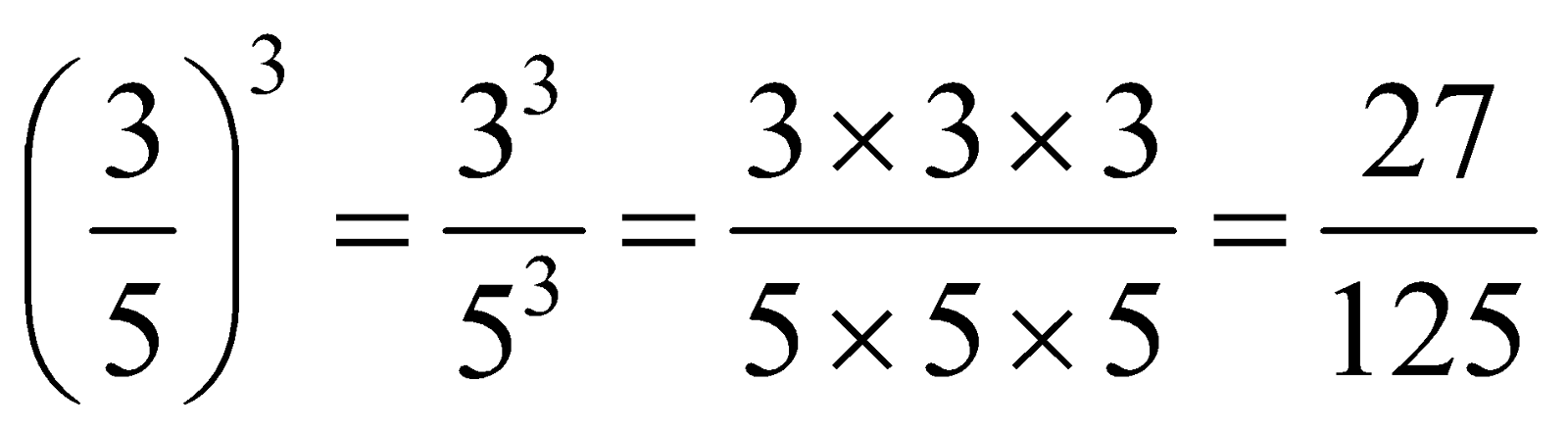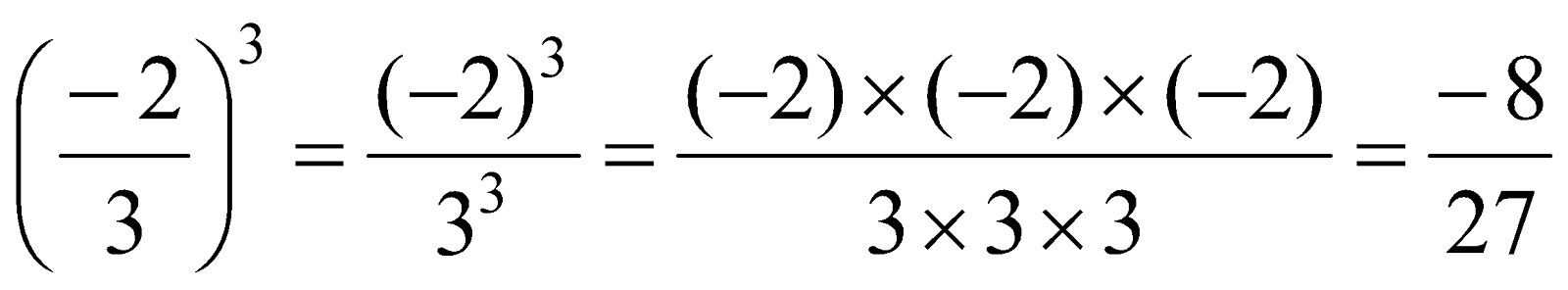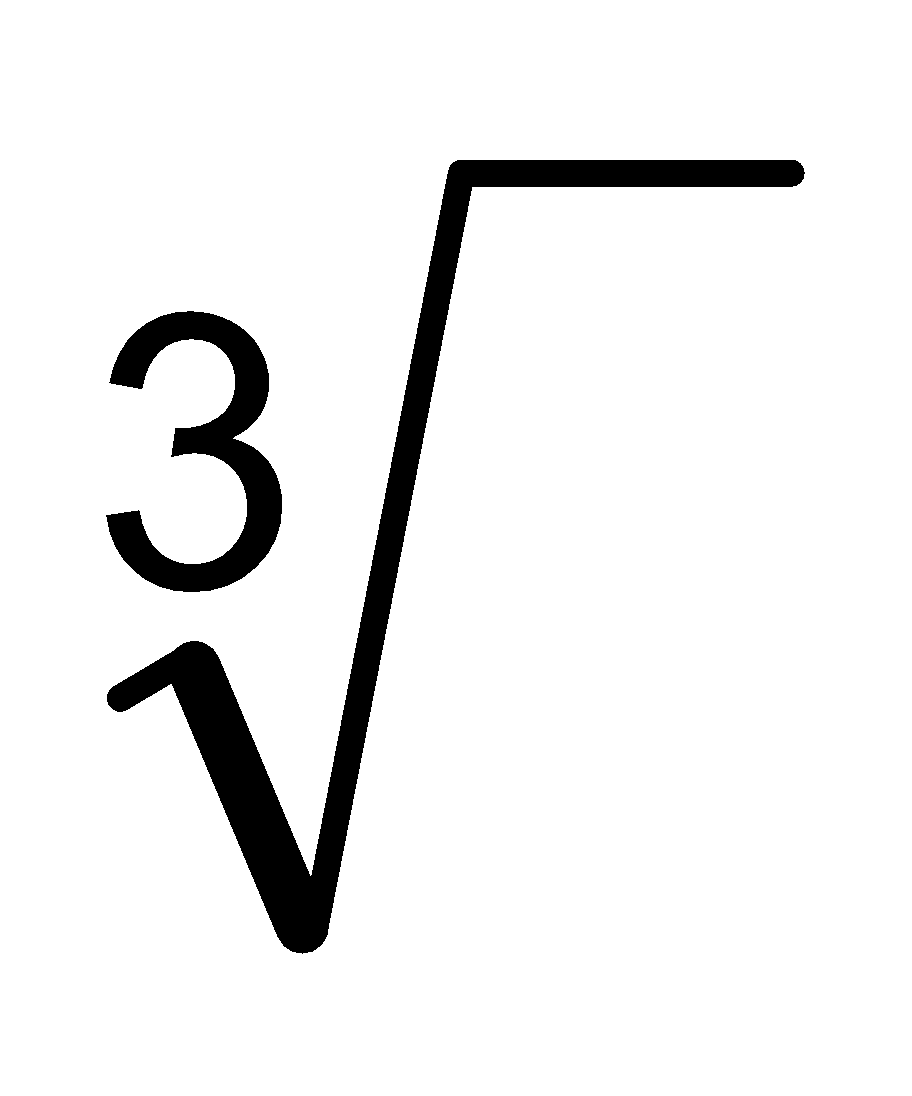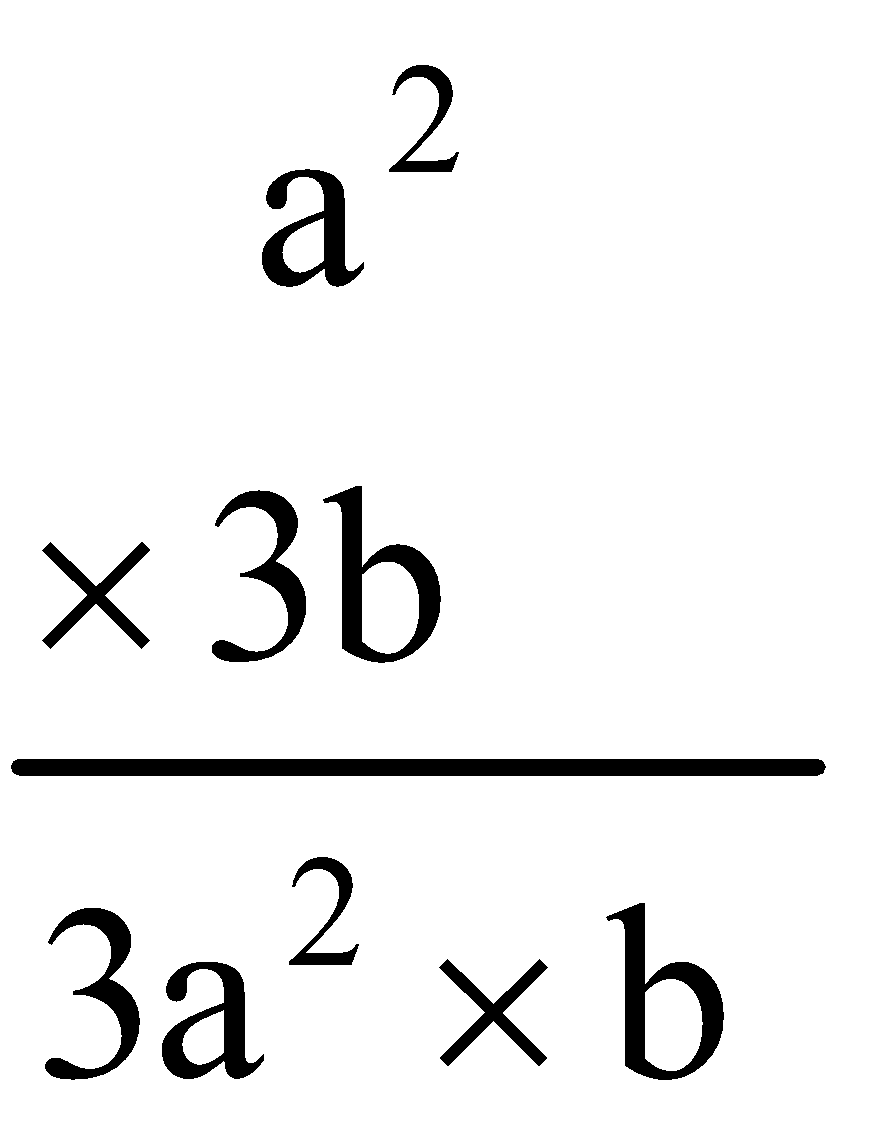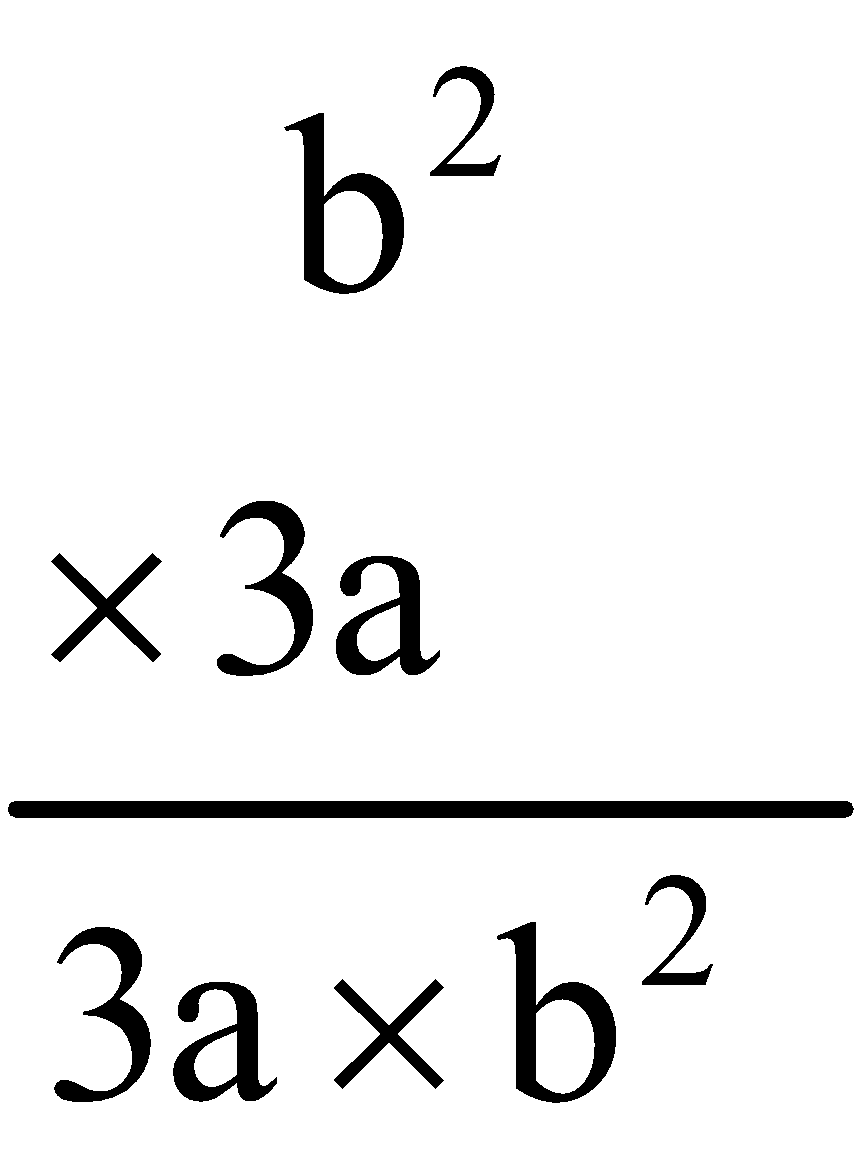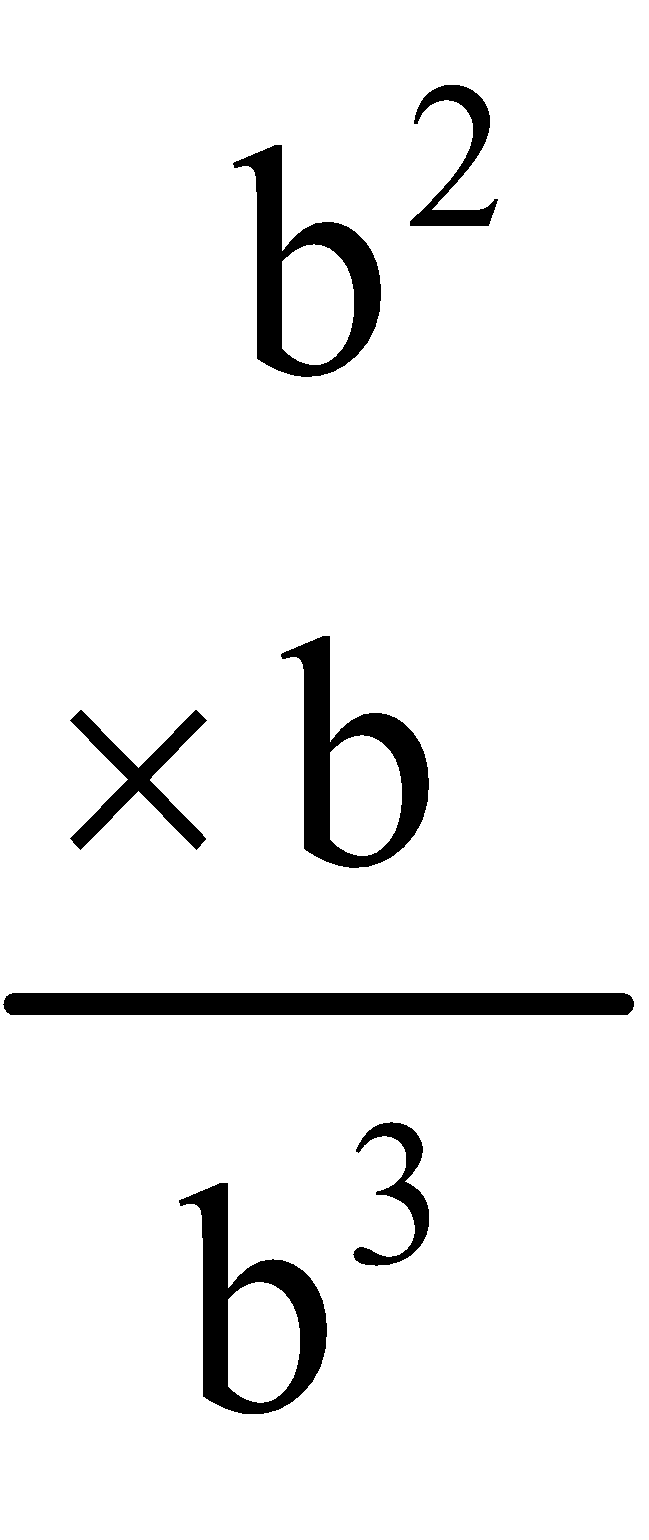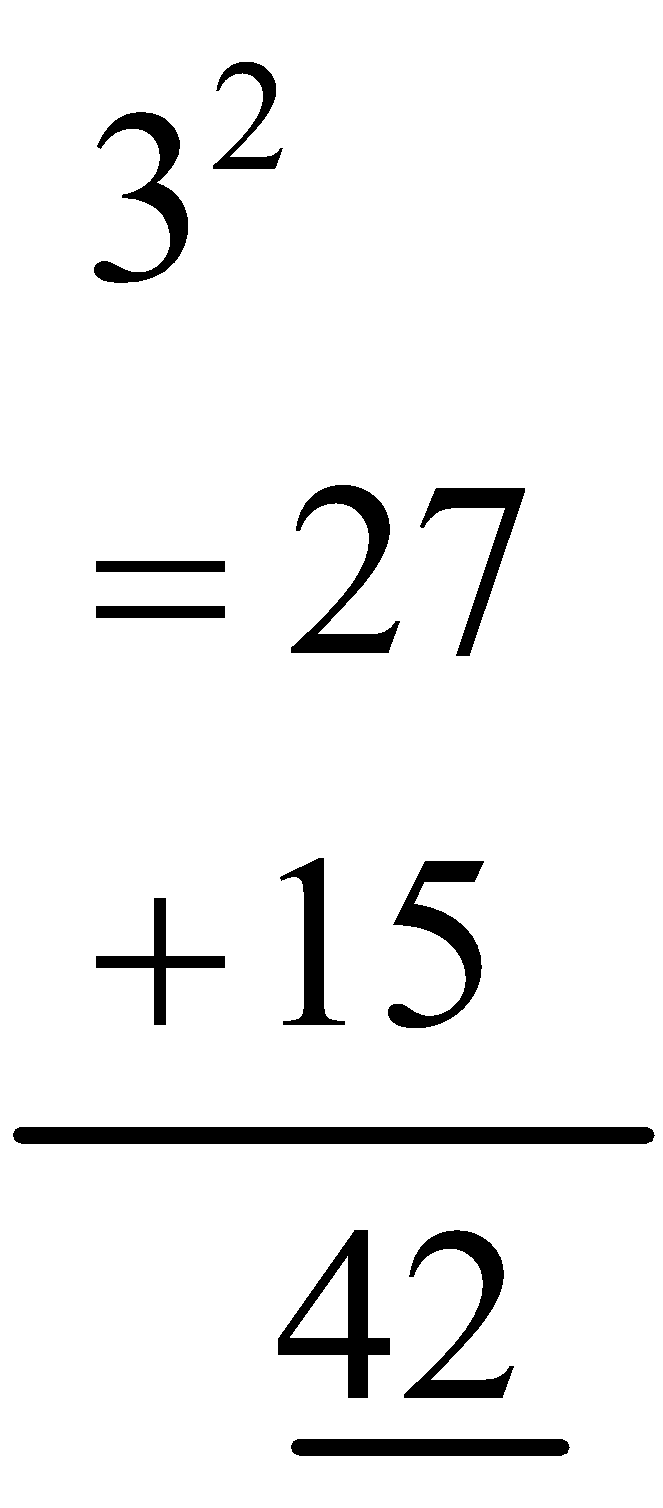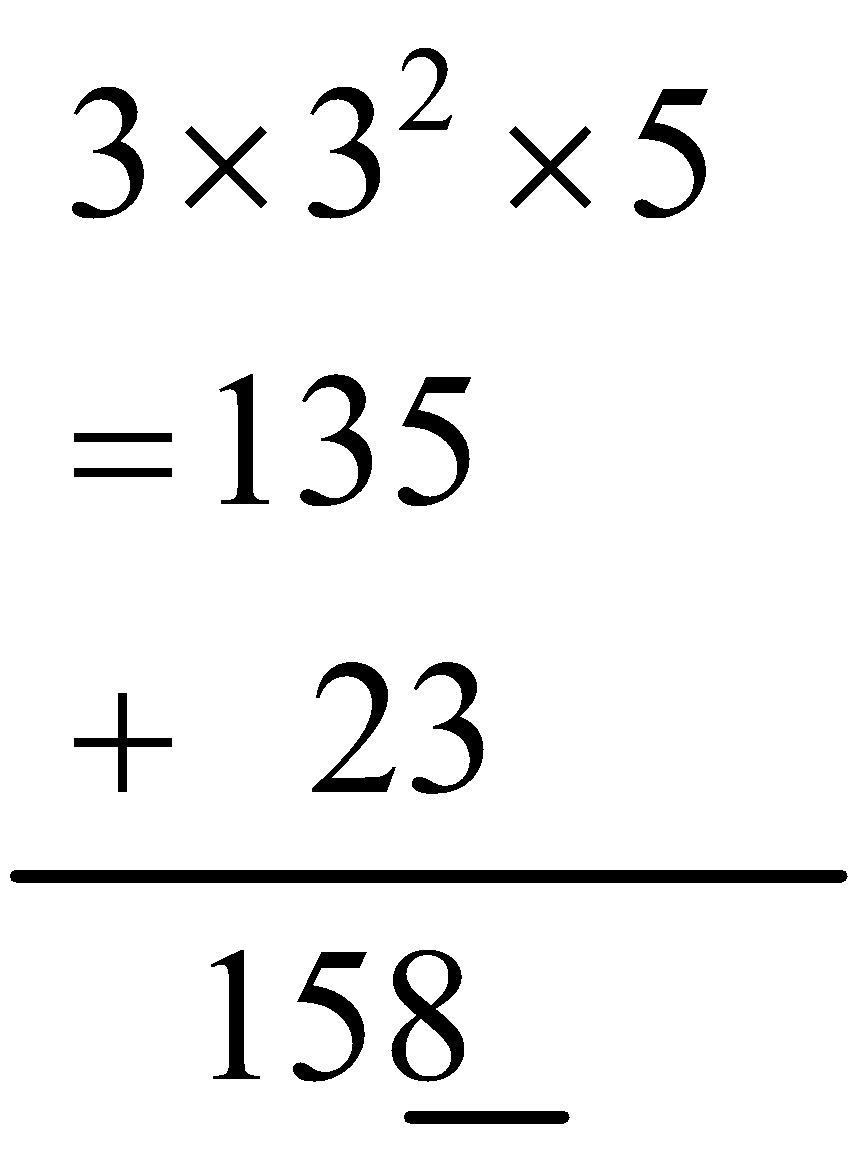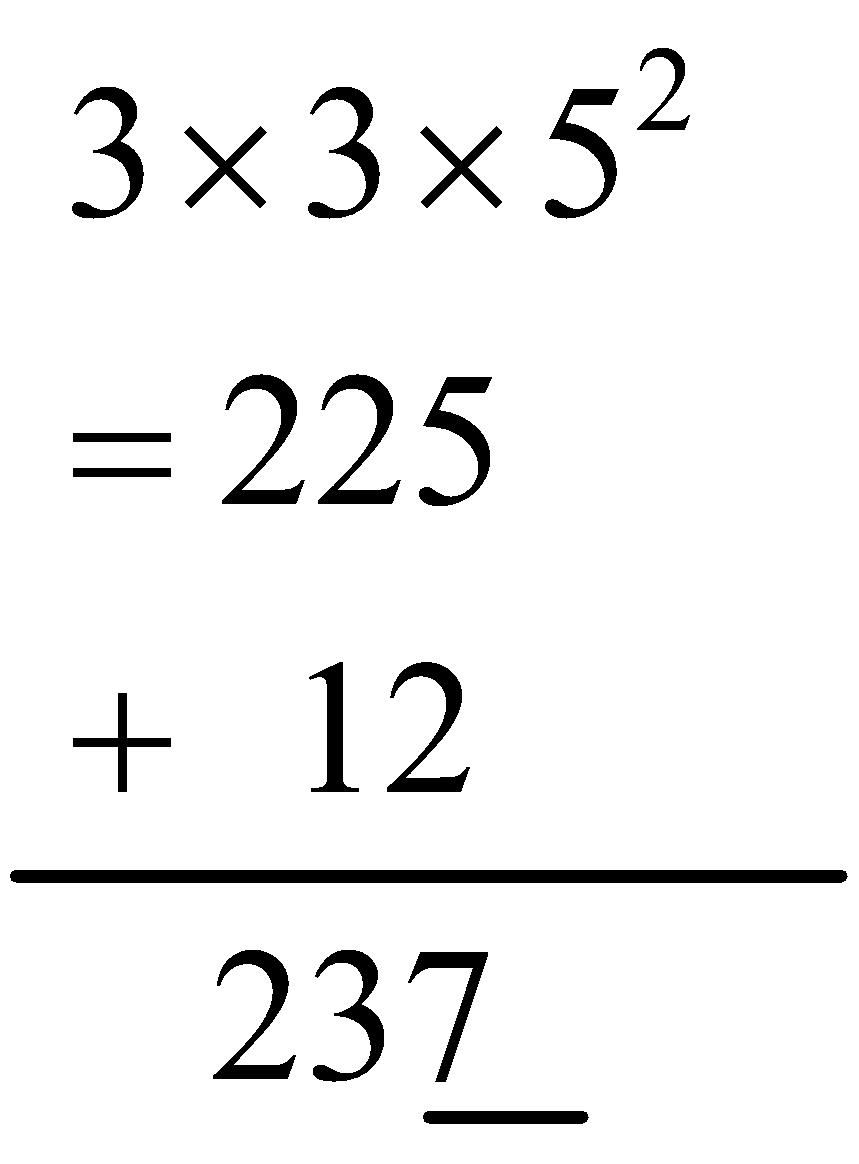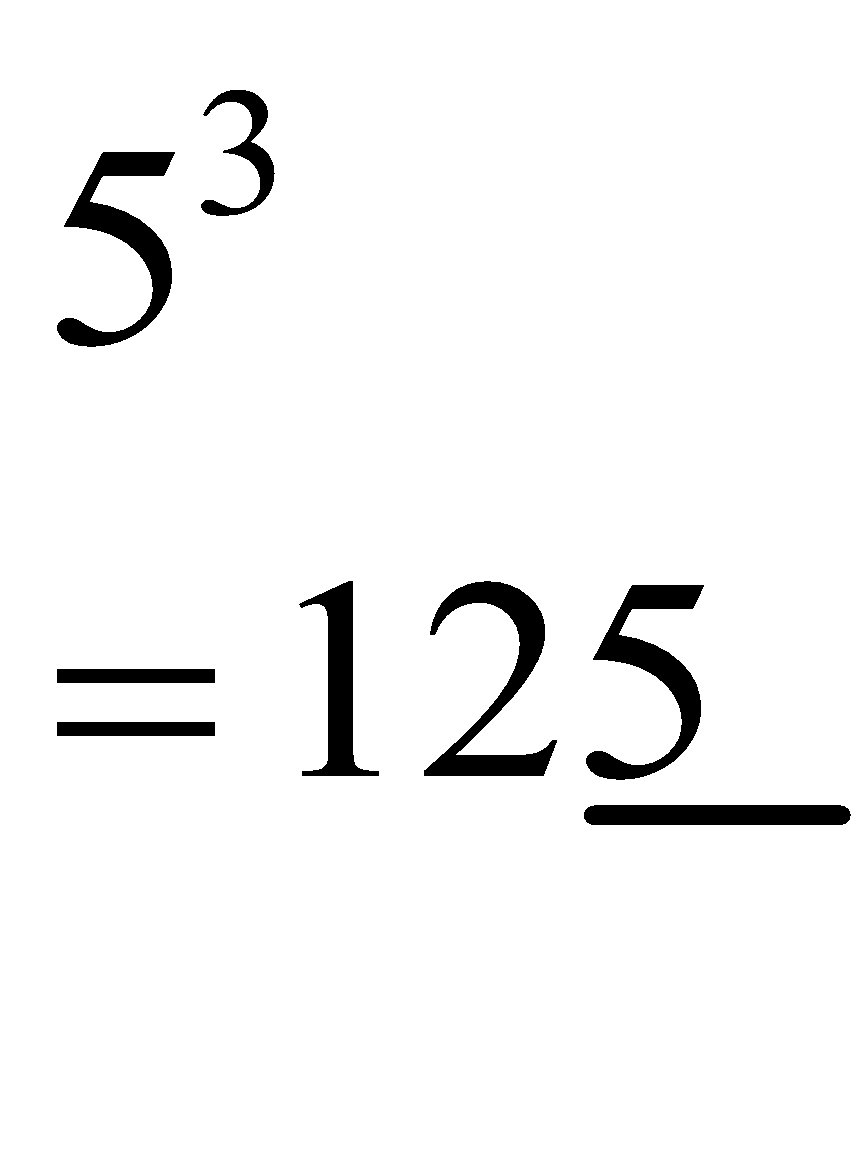Cubes and Cube Root

CUBE NUMBER:

A cube number (or a cube) is a number you can write as a product of three equal factors of natural numbers. Formula: k=a×a×a=a³ (k and a stand for integers.) 

Cube number results by multiplying an integer by itself three times. 
Formula: a×a×a=a³=k  (a and k stand for integers.) 

HOW TO CUBE A NUMBER:

To cube a number, just use it in a multiplication 3 times ...

question 1. What is 3 Cubed?

Solution: 3 Cubed = 3 × 3 × 3 = 27

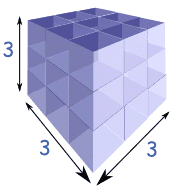
Note: we write down "3 Cubed" as 33 (the little "3" means the number appears three times in multiplying)

Some More Cubes:

PROPERTIES OF CUBE OF A NUMBER:

• The cube of every even number is even.
• The cube of every odd number is odd.
• Cubes of Negative Integers

The Cube of a negative integer is always negative.

Example:

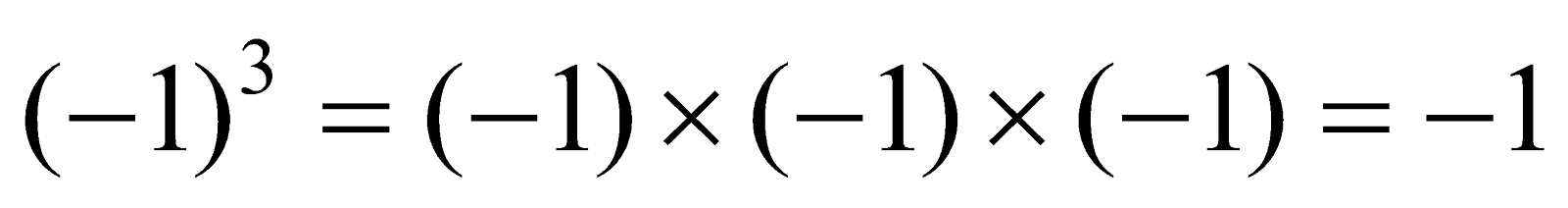
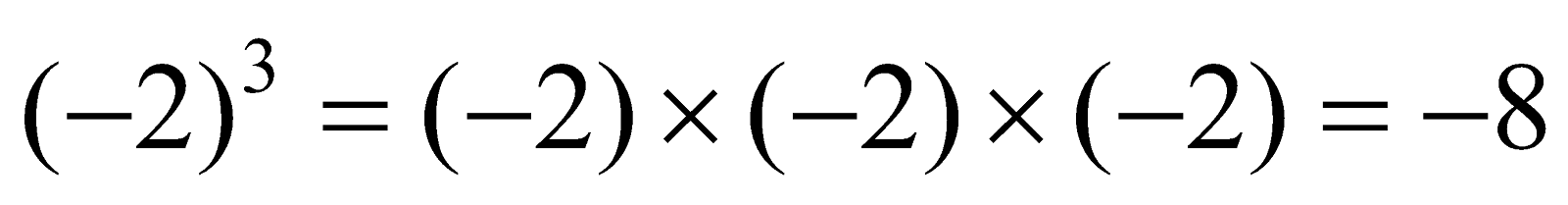
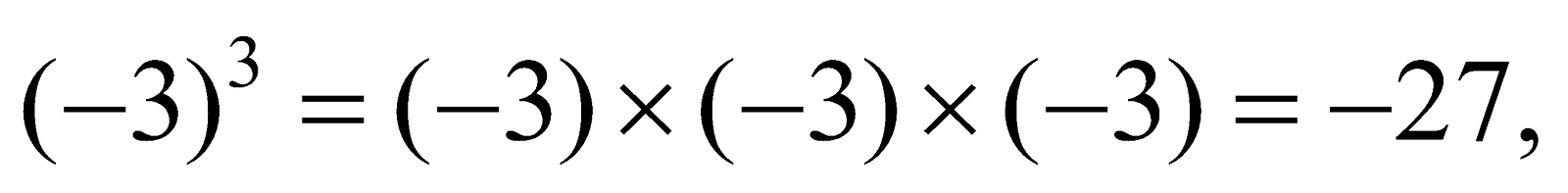etc.

• Cube of a Rational Number

We have,

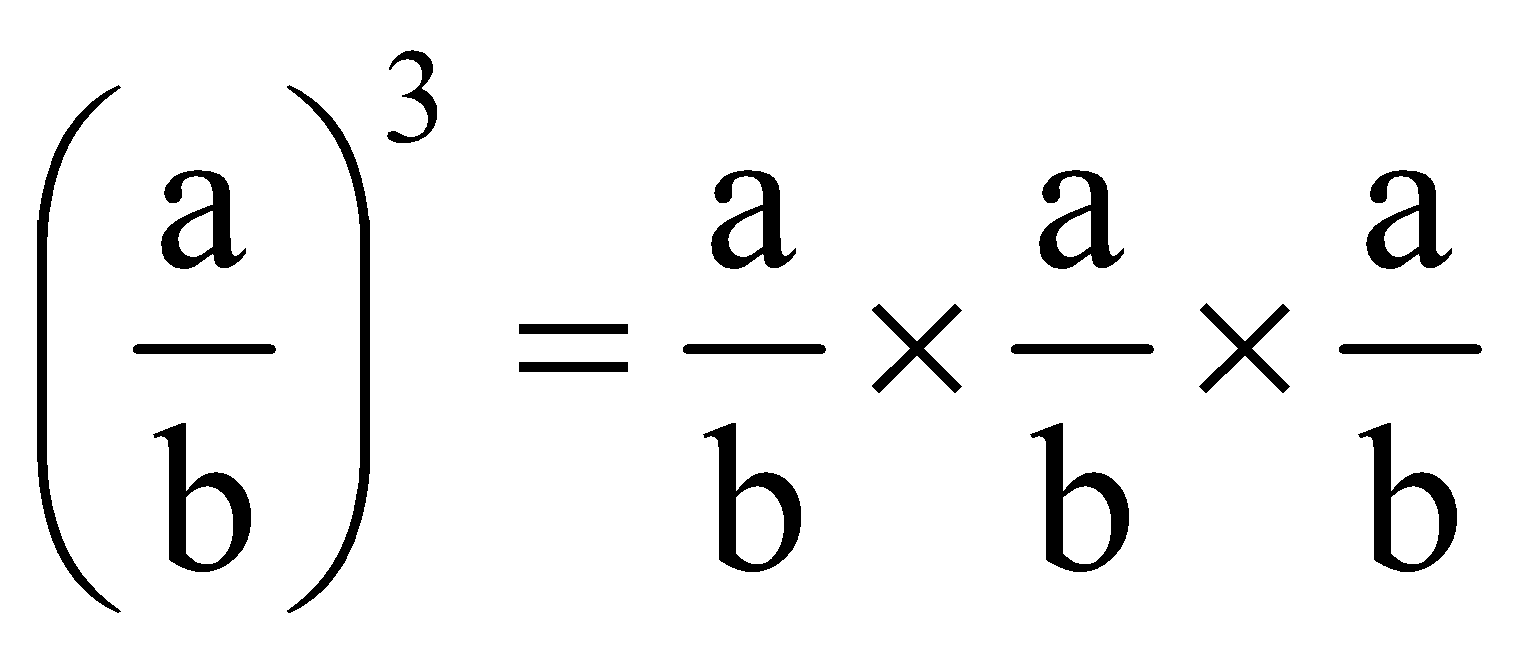
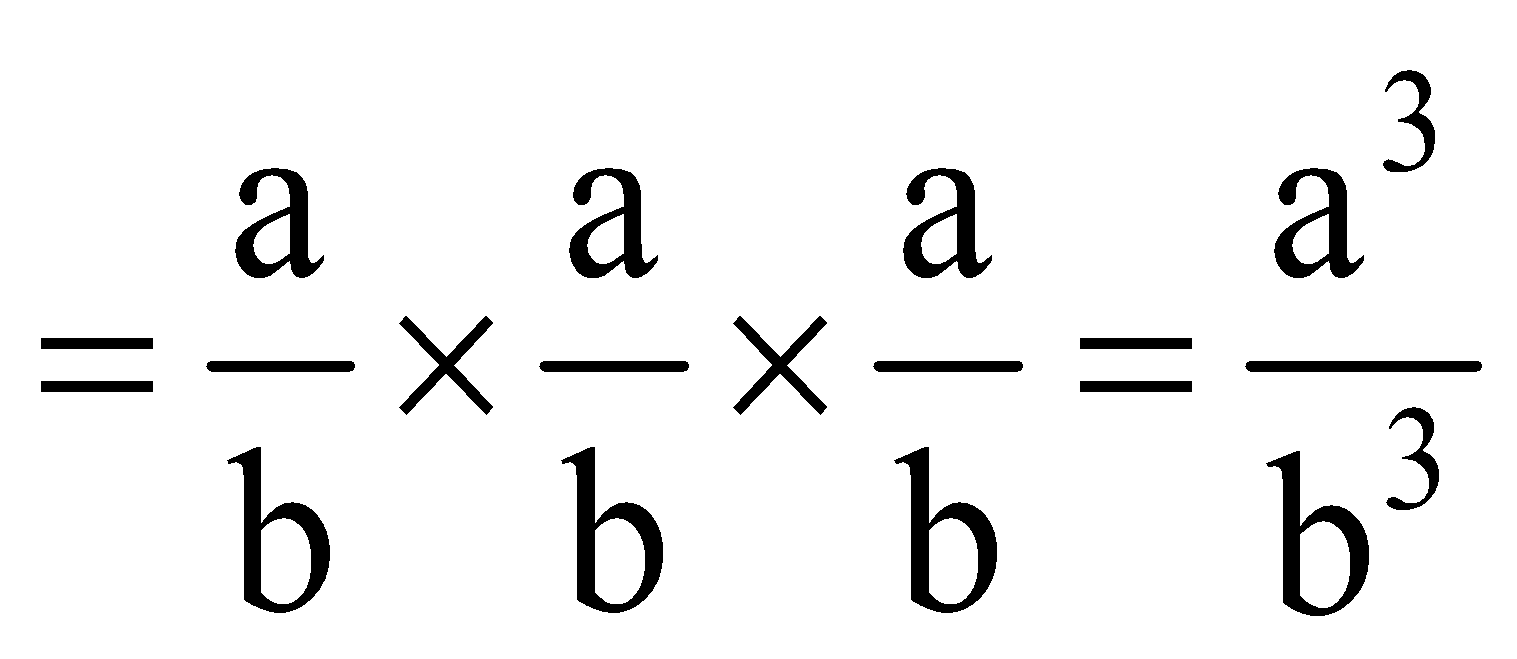
Hence,

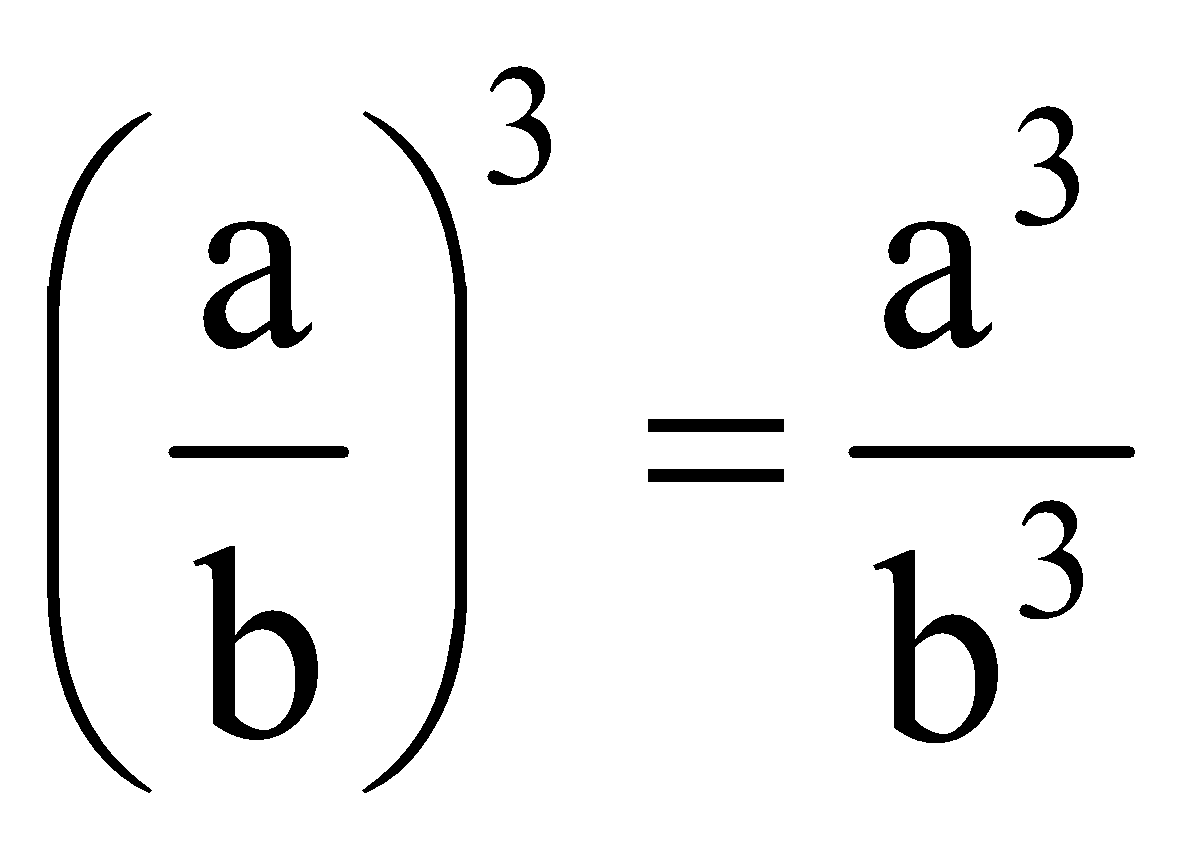
For example:

• 
• 

CUBE ROOT:

The cube roots of a number x are the numbers y which satisfy the equation

y3 = x

A cube root of a number, denoted 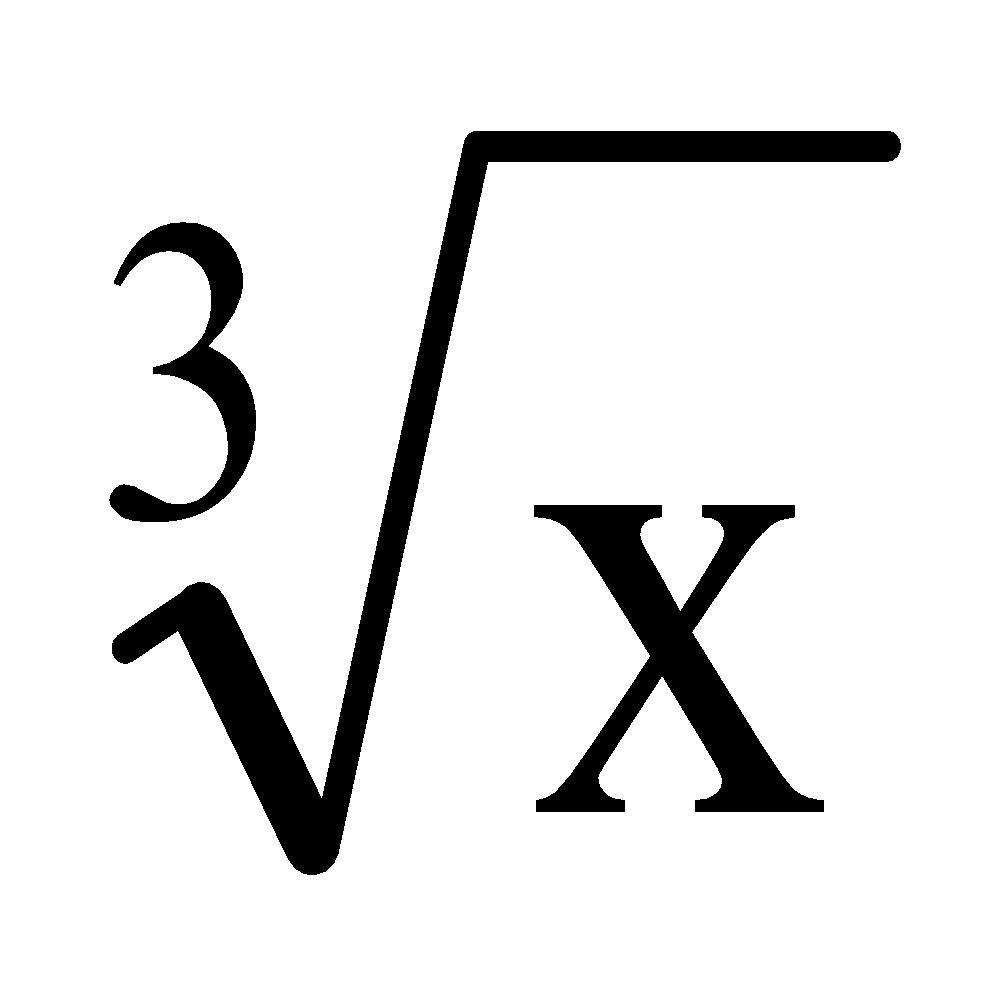 or x1/3, is a number a such that a3 = x. All  real numbers (except zero) have exactly one real cube root and a pair of roots.

For example, the real cube root of 8 is 2, because 23 = 8. 

A cube root goes the other direction:

3 cubed is 27, so the cube root of 27 is 3

The cube root of a number is ...... the special value that when cubed gives the original number.

The cube root of 27 is 3, because when 3 is cubed you get 27.

question 1. What is the Cube root of 125?

Solution: Well, we just happen to know that 125 = 5 × 5 × 5 (if you use 5 three times in a multiplication you will get 125) ...

... so the answer is 5

The Cube Root Symbol

You can use it like this: 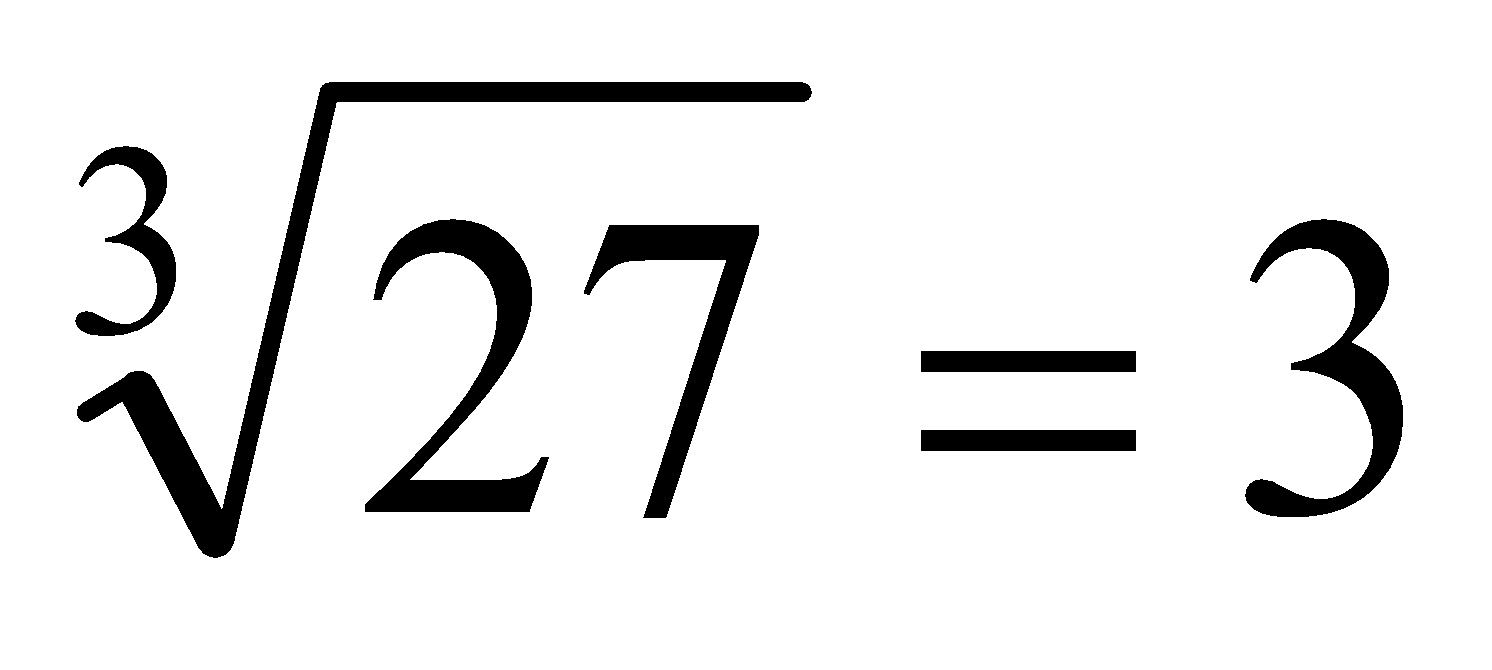(you would say "the cube root of 27 equals 3")

You Can Also Cube Negative Numbers

Have a look at this:

If you cube 5 you get 125: 5 × 5 × 5 = 125

If you cube -5 you get -125: -5 × -5 × -5 = -125

So the cube root of -125 is -5

Perfect Cubes

The Perfect Cubes are the cubes of the whole numbers:

PROPERTIES OF CUBE ROOT OF A NUMBER:

Cube Root Of A Negative Perfect Cube

Let a be positive integer. Then, (–a) is a negative integer. We know that

∴

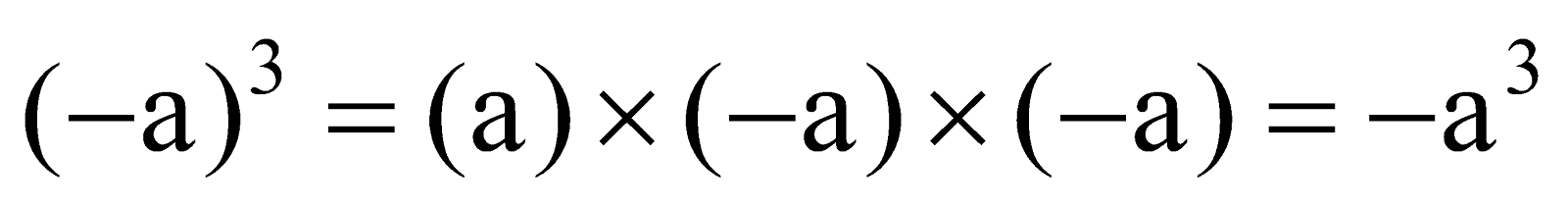
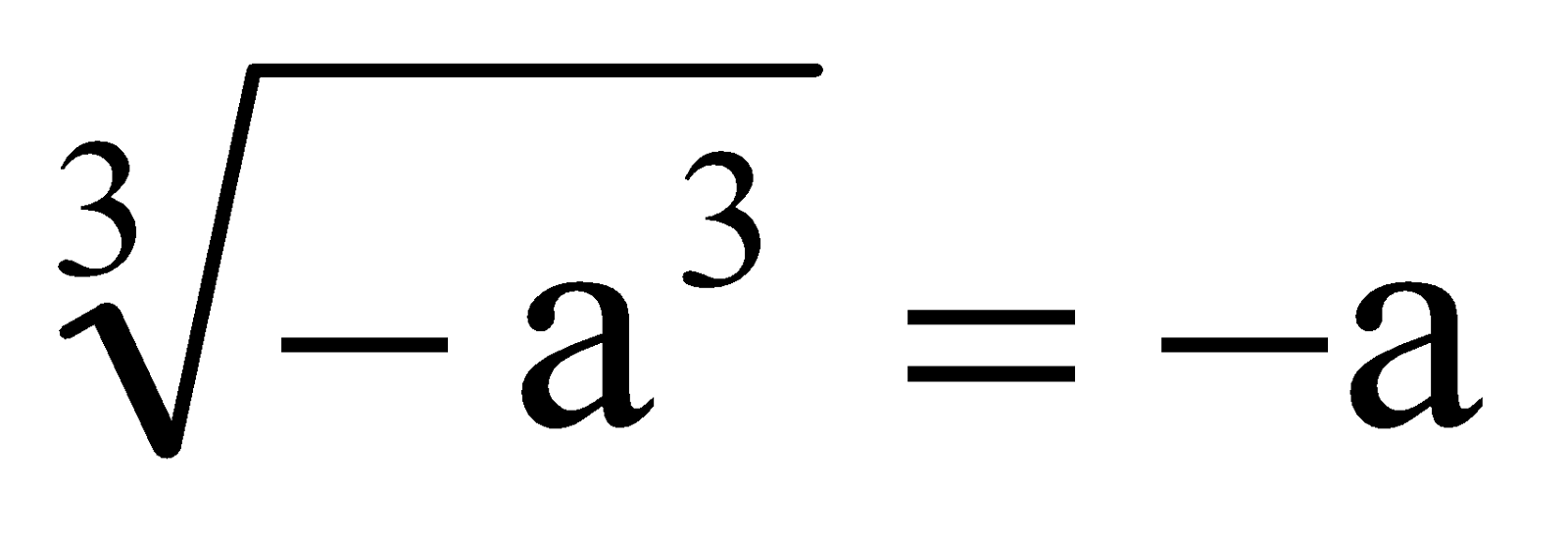
Thus, cube root of 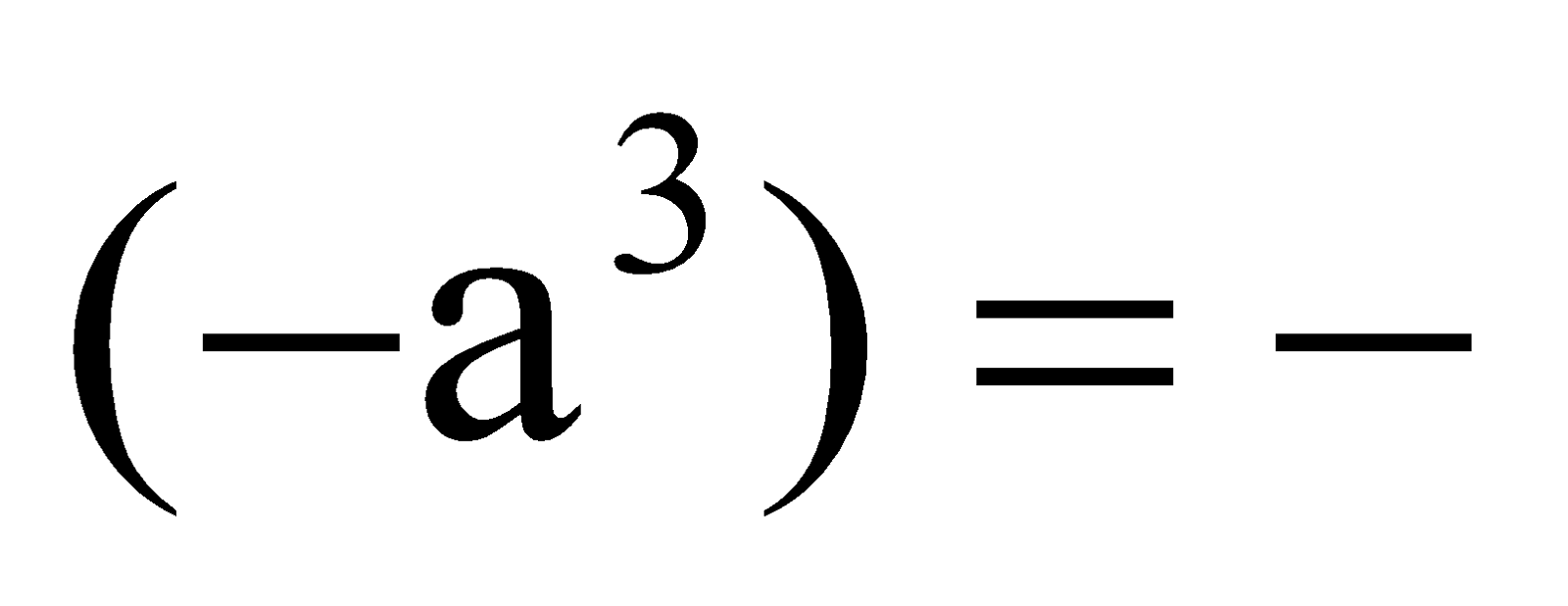(cube root of a3)

e.g.

∴

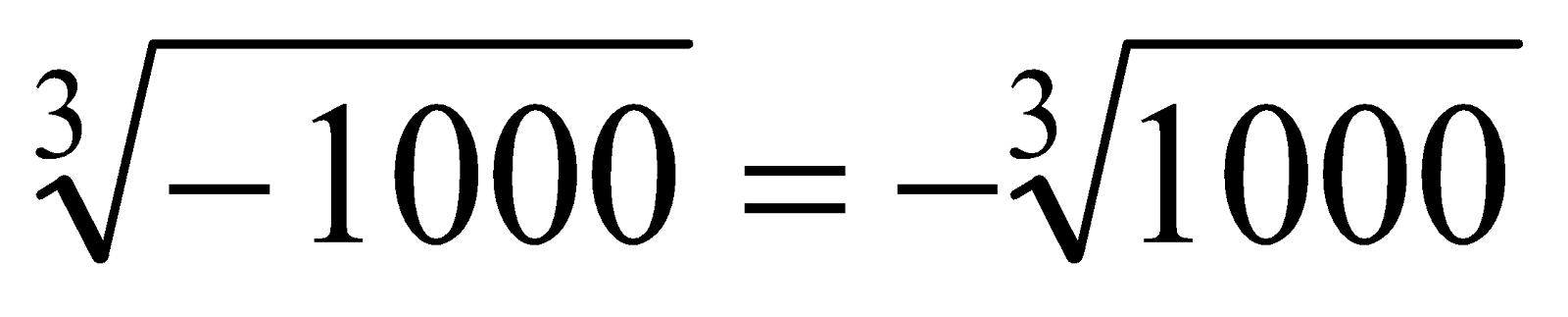
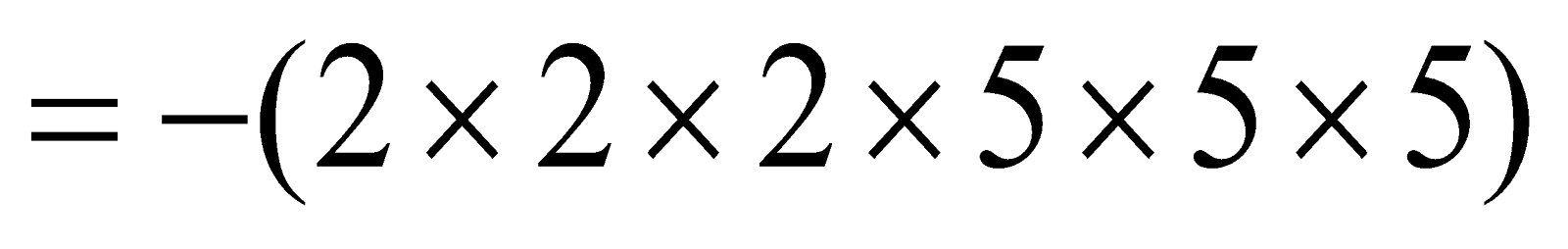
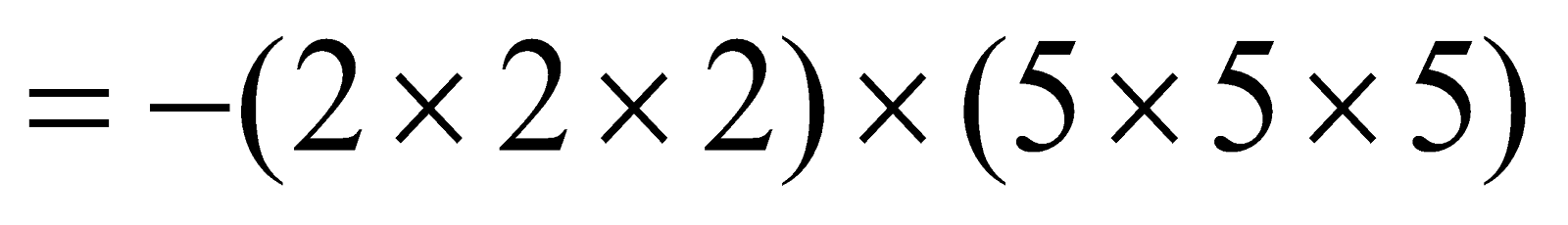
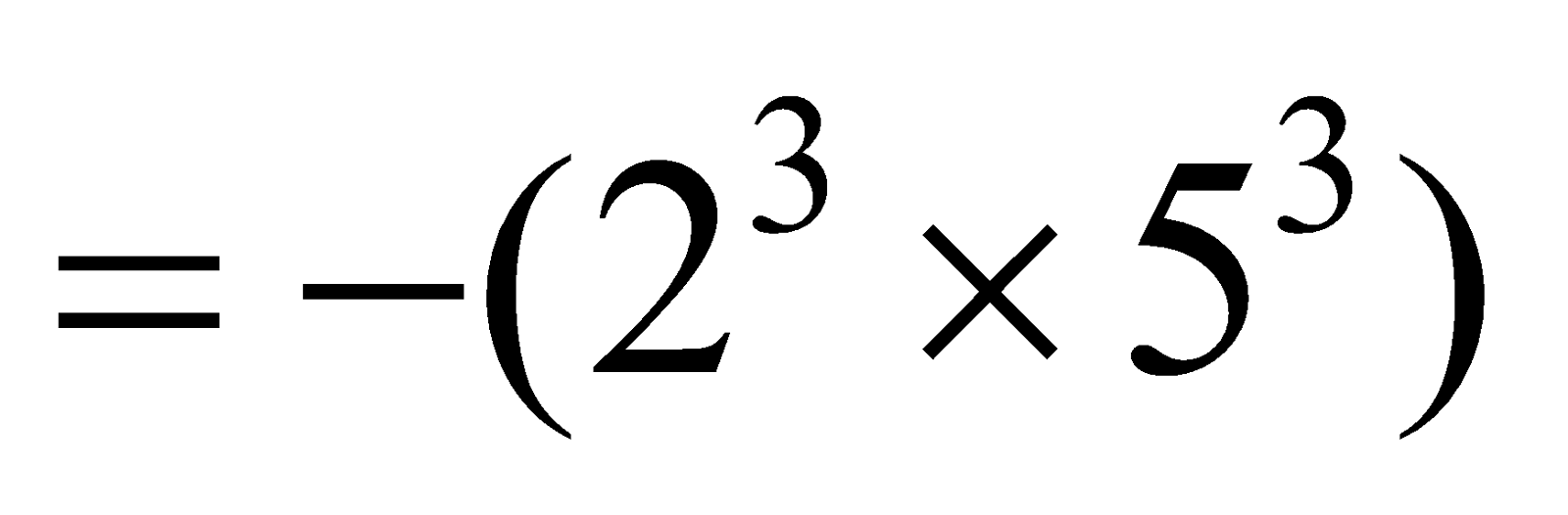
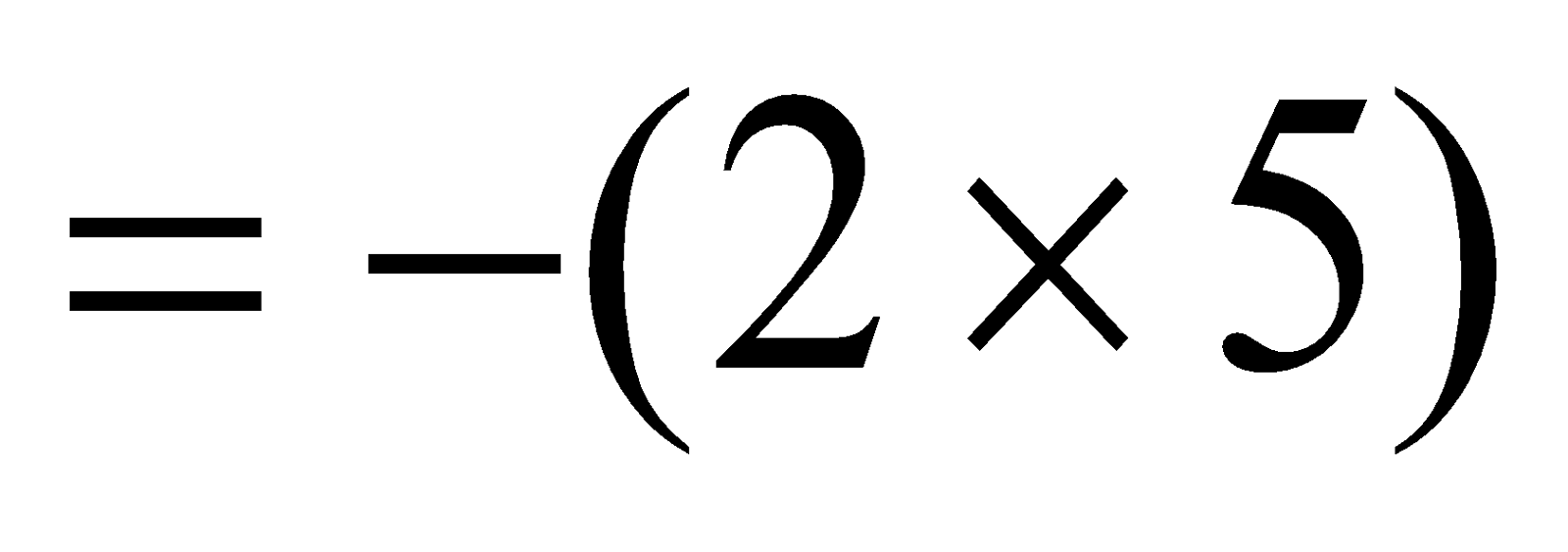
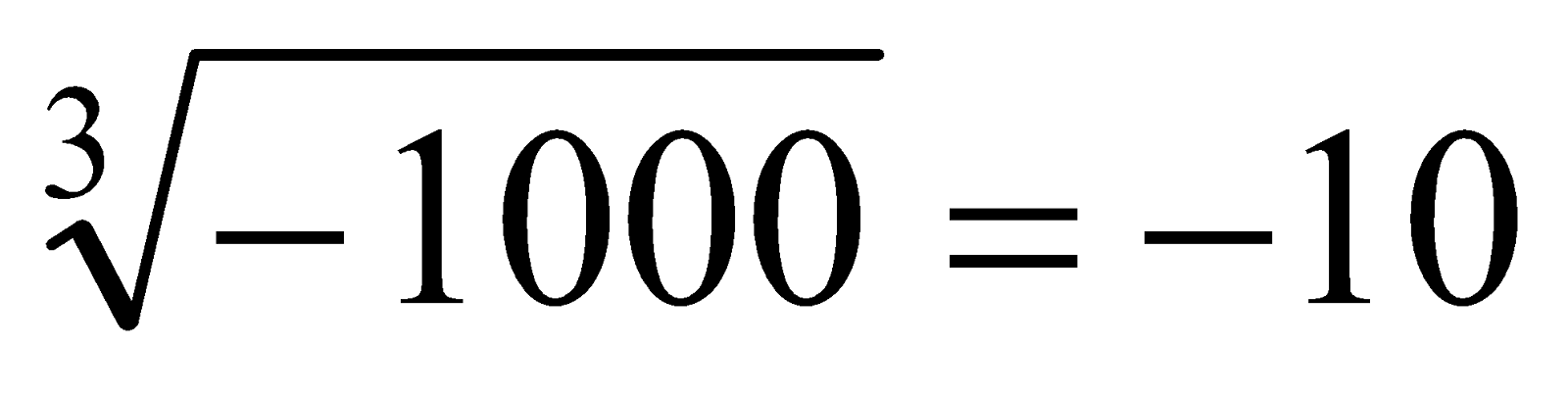
question 2. Cube Root Of A Product Of Integers

Solution: We have,

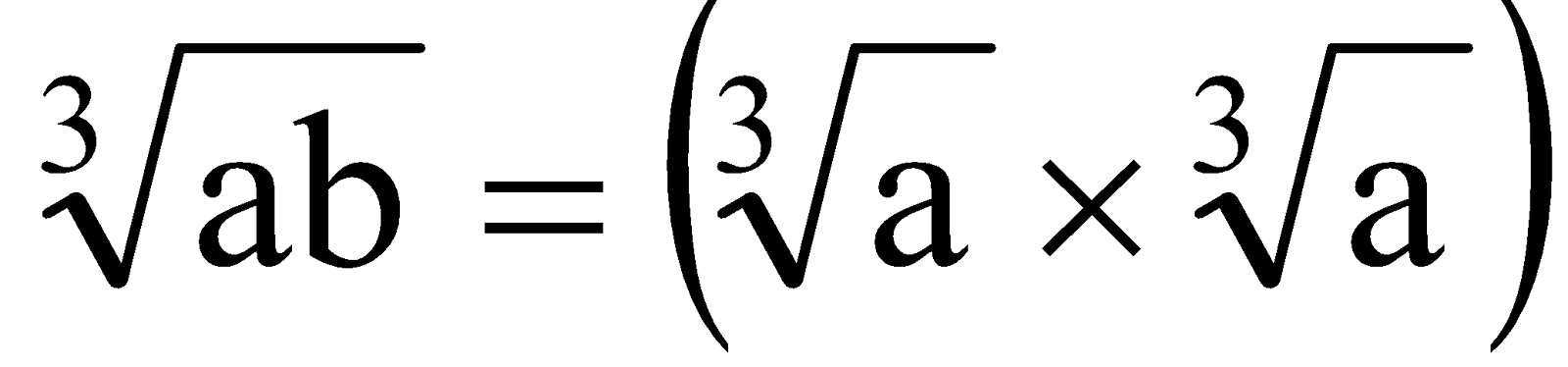
e.g.

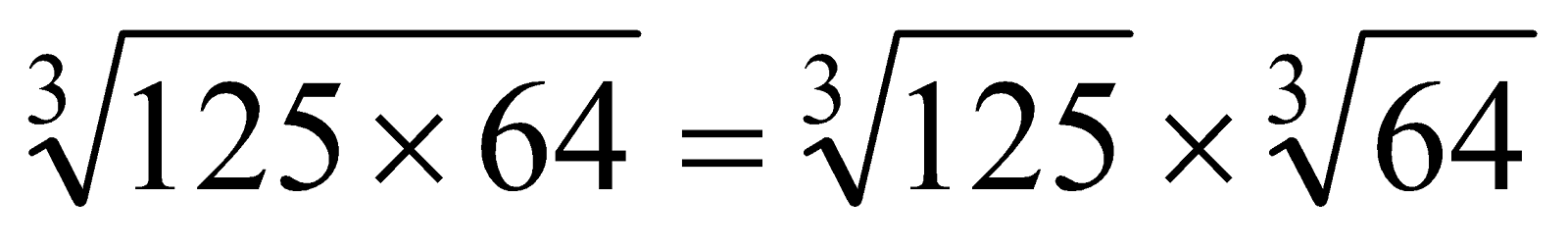
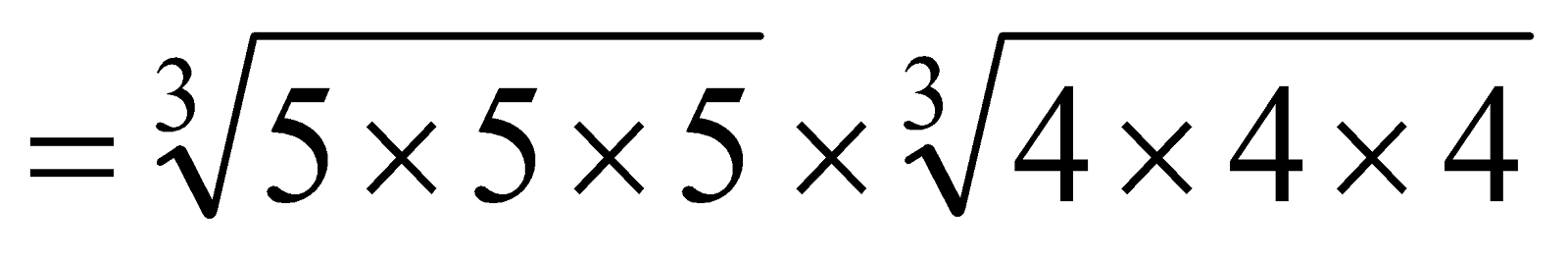
 = 5 x 4

= 20

question 3. Cube Root of A Rational Number

Solution: We have,

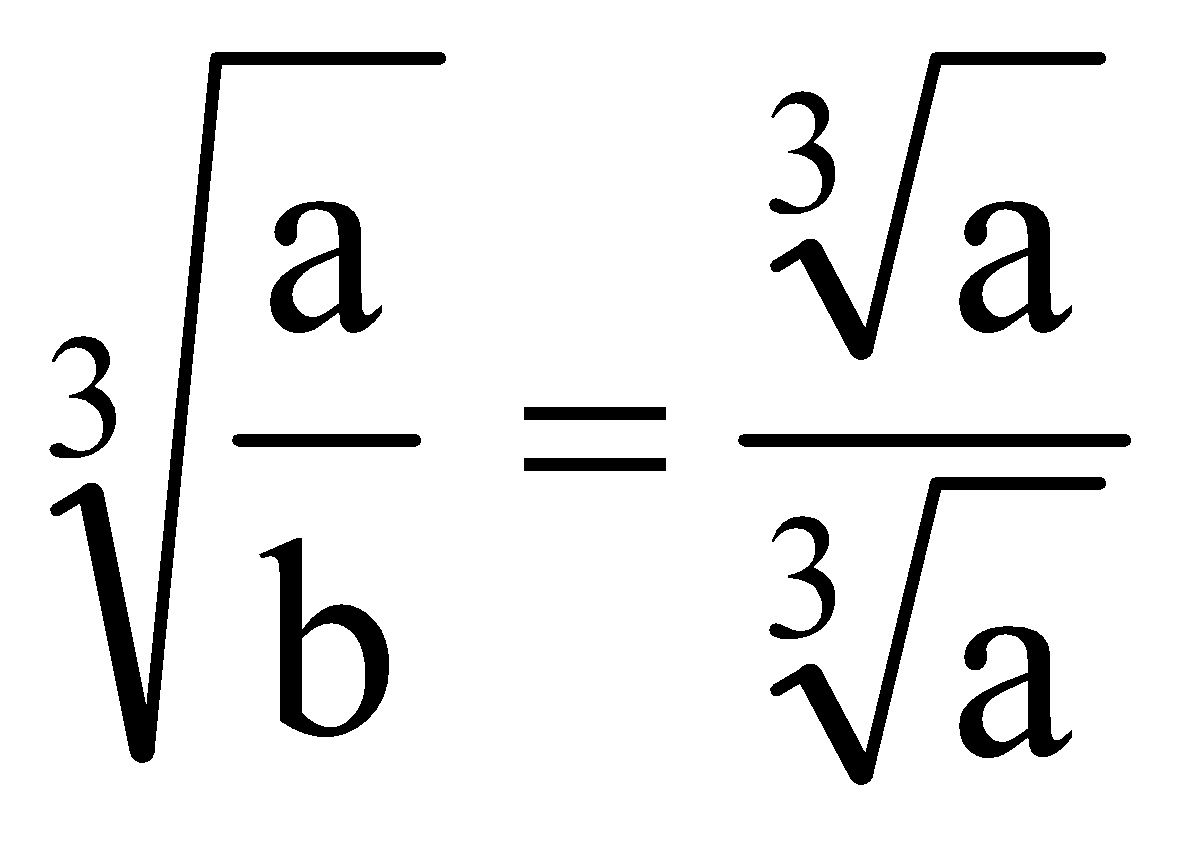
e.g.

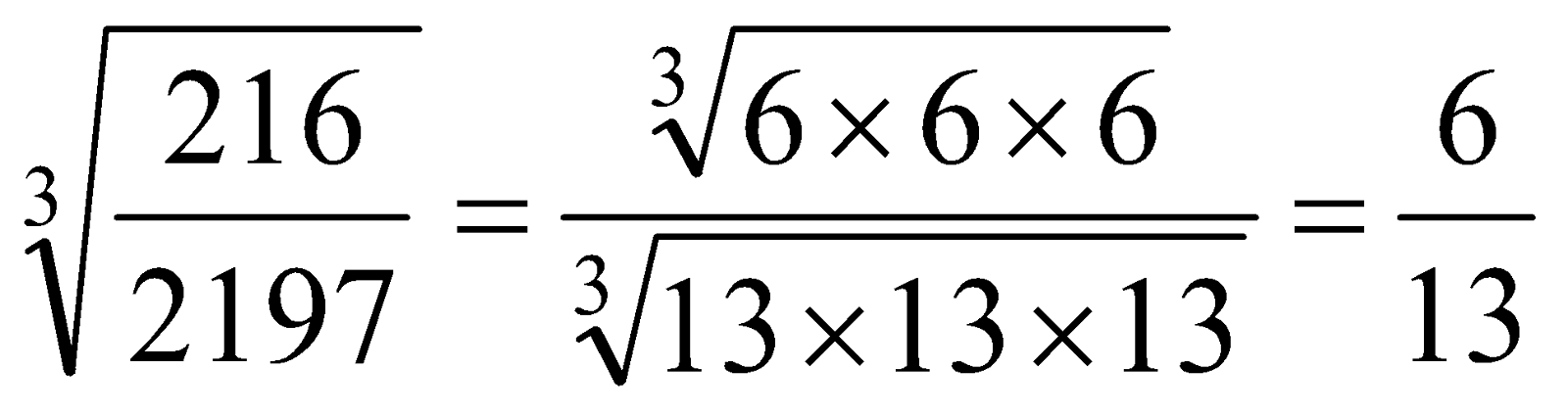
question 4. The cube root operation is not associative or distributive with addition or subtraction.

question 5. The cube root operation is associative with exponentiation and distributive with multiplication and division if considering only real numbers, but not always if considering complex numbers, for example:

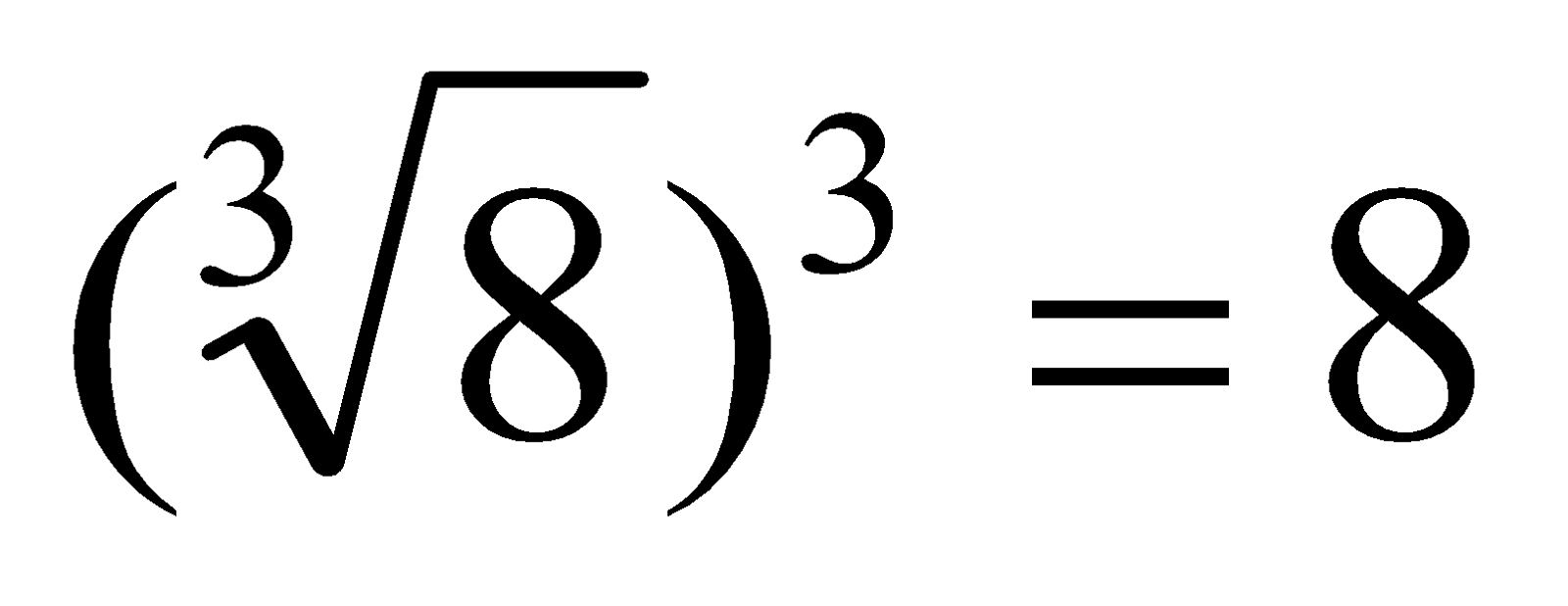
Properties of perfect cubes and cube roots:

 question 6.  The relationship between unit’s digit of cube and its cube root is as follows:

HOW TO FIND CUBE OF A GIVEN NUMBER:

Short-cut method for finding the cube of a two digit number:

We have,

For finding the cube of a two-digit number with the tens digit = a and the unit s digit = b, we made four columns, headed by 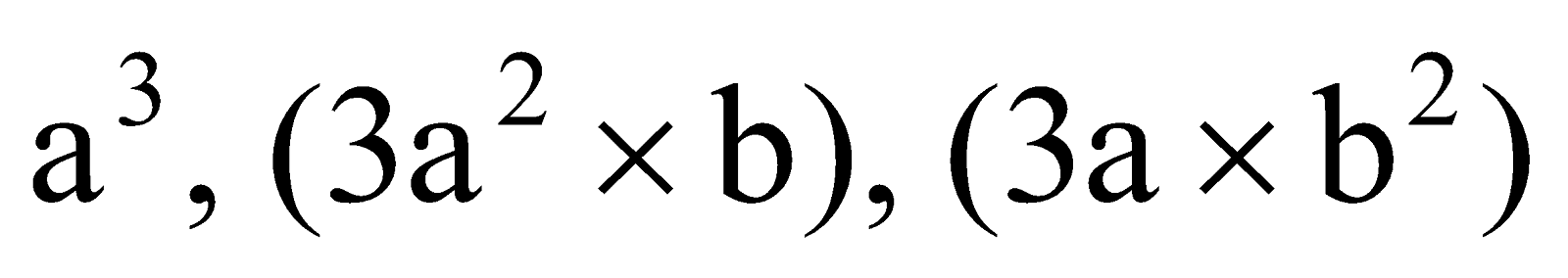and

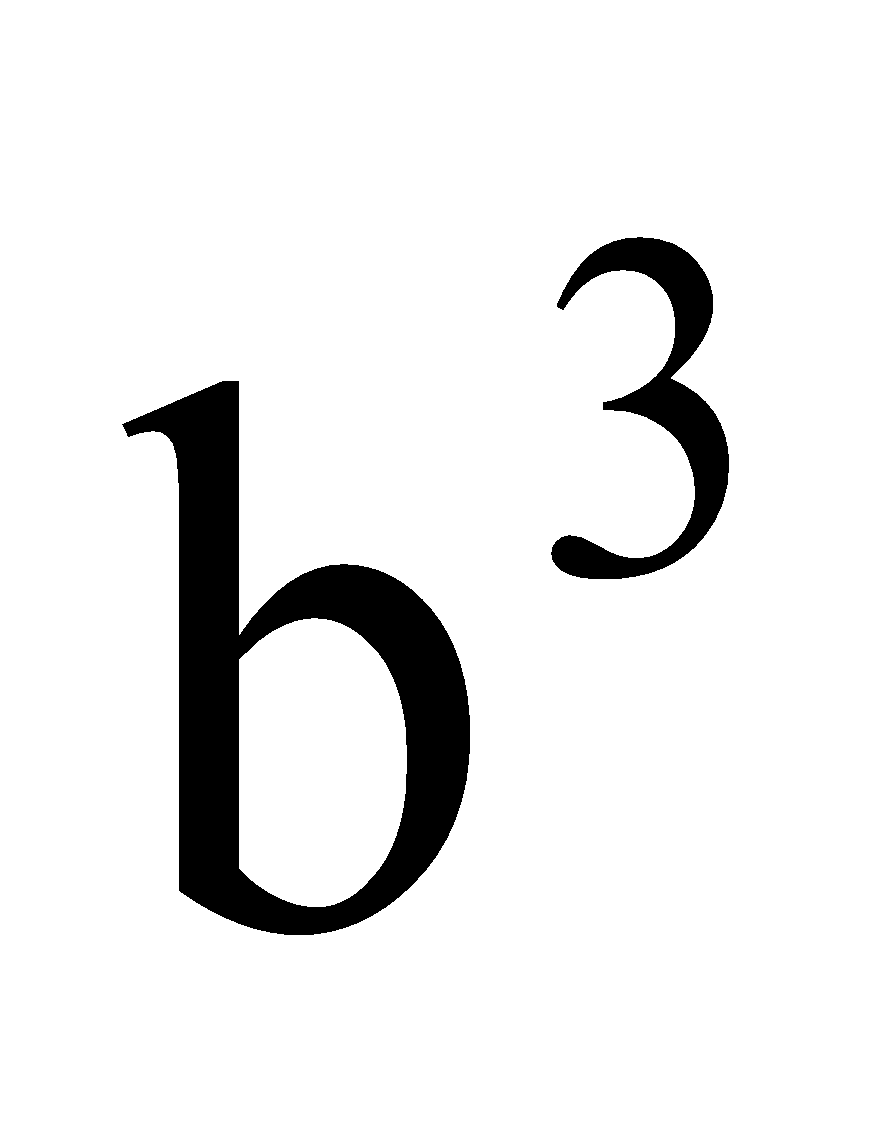
question 1. Find the cubes of 35 by the short-cut method. 

Solution: Here a = 3 and b = 5

∴

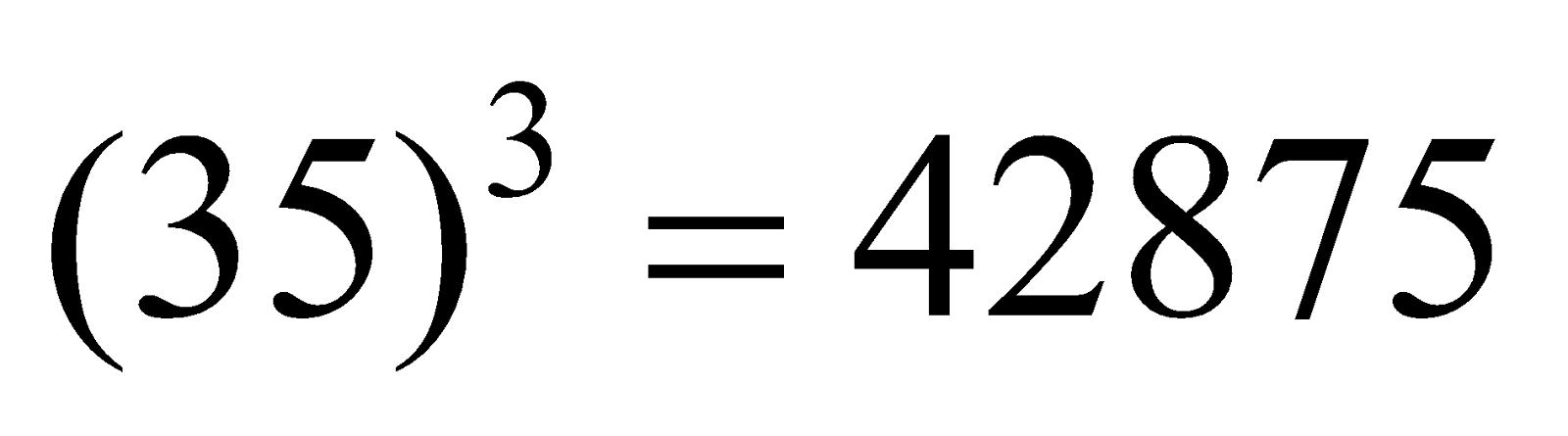
question 2. Find the smallest whole number by which each of the following numbers must be divided to obtain a perfect cube:

(a) 81 (b) 128 (c) 135 (d) 192 (e) 704

Solution:(a) 81 = 3 × 3 × 3 × 3

The prime factor 3 does not appear in a group of three. So if we divide 81 by 3, then the prime factorisation of the quotient will not contain 3.

81 ÷ 3 = 3 × 3 × 3

Hence the smallest whole number by which 81 should be divided to make it perfect cube is 3.

(b) 128 = 2 × 2 × 2 × 2 × 2 × 2 × 2  

The prime factor 2 does not appear in a group of three. So if we divide 128 by 2, then the prime factorisation of the quotient will not contain 2.

128 ÷ 2 = 2 × 2 × 2 × 2 × 2 × 2

Hence the smallest whole number by which 128 should be divided to make it perfect cube is 2.

(c) 135 = 3 × 3 × 3 × 5

In the factorization 5 appears only one time. So if we divide 135 by 5, then the prime factorization of the quotient will not contain 5.

135 ÷ 5 = 3 × 3 × 3

Hence the smallest whole number by which 135 should be divided to make it perfect cube is 5.

(d) 192 = 2 × 2 × 2 × 2 × 2 × 2 × 3

In the factorization 3 appears only one time. So, if we divide 192 by 3, then the prime factorization of the quotient will not contain 3.

192 ÷ 3 = 2 × 2 × 2 × 2 × 2 × 2

Hence, the smallest whole numbers by which 192 should be divided to make it perfect cube is 3.

(e) 704 = 2 × 2 × 2 × 2 × 2 × 2 × 11

In the factorization 11 appears only one time. So if we divide 704 by 11, then the prime factorization of the quotient will not contain 11.

704 ÷ 11 = 2 × 2 × 2 × 2 × 2 × 2

Hence the smallest whole number by which 704 should be divided to make it perfect cube is 11.

question 4. State true or false.

(a) Cube of any odd number is even

(b) A perfect cube does not end with two zeros

(c) If square of a number ends with 5, then its cube ends with 25.

(d) There is not perfect cube which ends with8.

(e) The cube of a two digit number may be a three digit number.

(f) The cube of a two digit number may have seven or more digits.

(g) The cube of a single digit number may be a single digit number.

Solution: (a) False (b) True (c) True (d) False

(e) False (f) False (g) True

question 5. Is 53240 a perfect cube? If not, then by which smallest natural number should 53240 be divided so that the quotient is a perfect cube?

Solution: 53240 = 2 × 2 × 2 × 11 × 11 × 11 × 5

The prime factor 5 does not appear in a group of three, So, 53240 is not a perfect cube. In the factorization 5 appears only one time. If we divide the number by 5, then the prime factorization of the quotient will not contain 5.

Hence the smallest number by which 53240 should be divided to make it a perfect cube is 5.

The perfect cube in that case is = 10648.

question 6. Observe the following pattern of sums of odd numbers:

1 = 1 = 13

3 + 5 = 8 = 23

7 + 9 + 11 = 27 = 33

13 + 15 + 17 + 19 = 64 = 43

21 + 23 + 25 + 27 + 29 = 125 = 53

31 + 33 + 35 + 37 + 39 + 41= 216 = 63

——————— = 343 = 73

——————— = 512 = 83

——————— = 729 = 93

——————— = 1000 = 103

Express the following numbers as the sum of odd numbers using the above pattern?

(a) 6³

(b) 7³

(c) 8³

Solution: According to above pattern, we have

(a)

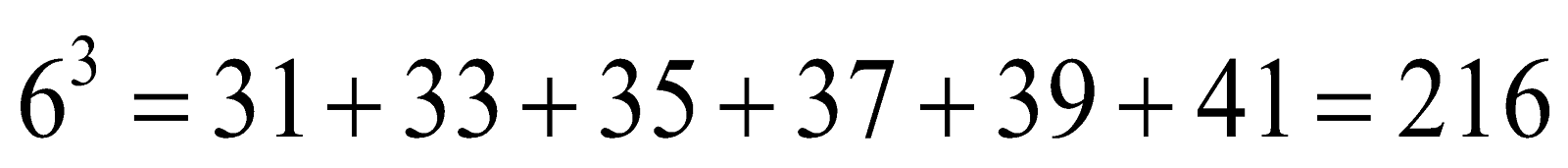
(b)

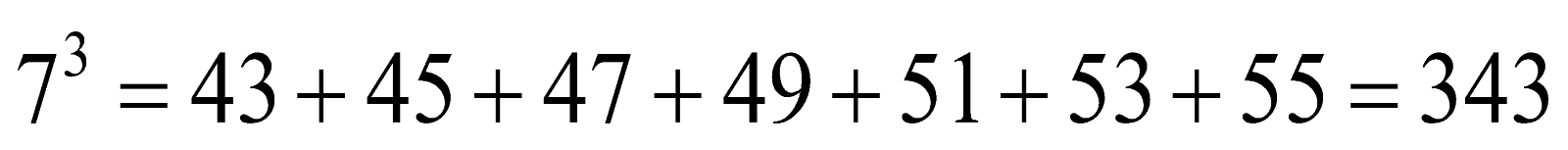
(c)

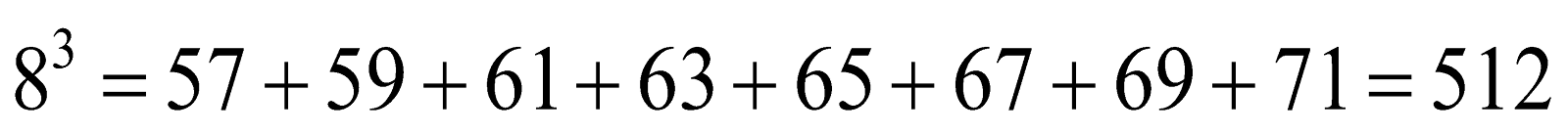
NCERT solutions for class 8 Maths  prepared by Physics Wallah will help you to solve your NCERT text book exercise.