Basic Proportionality Theorem (Thales Theorem)
THEOREM 1:
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
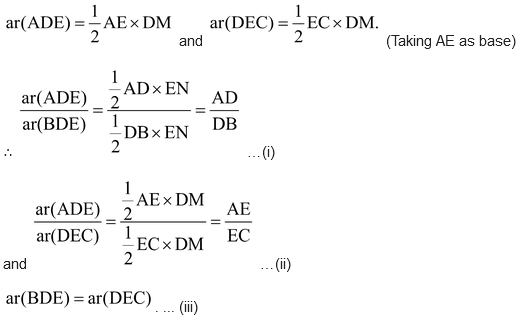
Given: A triangle ABC in which a line parallel to side BC intersects other two sides AB and AC at D and E respectively.
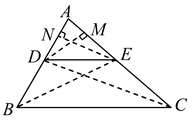
To prove:
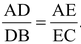
Construction:
Join BE and CD and draw DM ⊥ AC and EN ⊥ AB.
Proof: area of Δ ADE
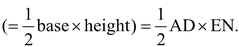
(Taking AD as base)
So,
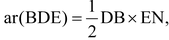[The area of Δ ADE is denoted as ar (ADE)].
Similarly,
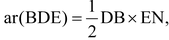
[Δ BDE and DEC are on the same base DE and between the same parallels BC and DE.]
Therefore, from (i), (ii) and (iii), we have:
.
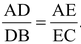Corollary: From above equation we have
.
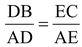Adding '1' to both sides we have
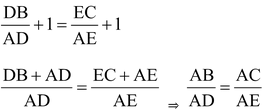
THEOREM 2:
(Converse of BPT theorem) If a line divides any two sides of a triangle in the same ratio, prove that it is parallel to the third side.
Given: In ΔABC, DE is a straight line such that
.
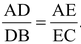To prove: DE || BC.
Construction:
If DE is not parallel to BC, draw DF meeting AC at F.
Proof: In ΔABC, let DF || BC
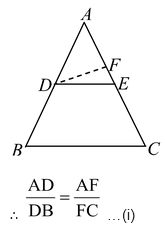
[∴ A line drawn parallel to one side of a Δ divides the other two sides in the same ratio.]
But
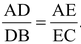. …(ii) [given]
From (i) and (ii), we get
.
⇒ FC = EC.
It is possible only when E and F coincide
Hence, DE || BC.
SOME IMPORTANT RESULTS AND THEOREMS:
(i) The internal bisector of an angle of a triangle divides the opposite side internally in the ratio of the sides containing the angle.
(ii) In a triangle ABC, if D is a point on BC such that D divides BC in the ratio AB : AC, then AD is the bisector of ∠A.
(iii) The external bisector of an angle of a triangle divides the opposite sides externally in the ratio of the sides containing the angle.
(iv) The line drawn from the mid-point of one side of a triangle parallel to another side bisects the third side.
(v) The line joining the mid-points of two sides of a triangle is parallel to the third side.
(vi) The diagonals of a trapezium divide each other proportionally.
(vii) If the diagonals of a quadrilateral divide each other proportionally, then it is a trapezium.
(viii) Any line parallel to the parallel sides of a trapezium divides the non-parallel sides proportionally.
(ix) If three or more parallel lines are intersected by two transversal, then the intercepts made by them on the transversal are proportional.
Question 1.
In a ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC. If AD = 4x – 3, AE = 8x – 7, BD = 3x – 1 and CE = 5x – 3, find the value of x.
Solution:
In ΔABC, we have
DE||BC.
∴
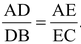. [By Basic Proportionality Theorem]
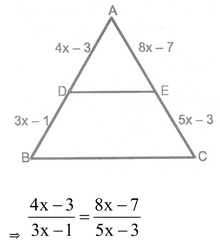
⇒ 20x
2
– 15x – 12x + 9 = 24x
2
– 21x – 8x + 7
⇒ 20x
2
– 27x + 9 = 24x
2
– 29x + 7
⇒ 4x2 – 2x – 2 = 0
⇒ 2x2 – x – 1 = 0
⇒ (2x + 1) (x – 1) = 0
⇒ x = 1 or x = –1/2
So, the required value of x is 1.
[x = - 1/2 is neglected as length cannot be negative].
Question 2.
D and E are respectively the points on the sides AB and AC of a ΔABC such that AB = 12 cm, AD = 8 cm, AE = 12 cm and AC = 18 cm, show that DE || BC.
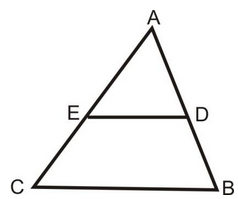
Solution:
We have,
AB = 12 cm, AC = 18 m, AD = 8 cm and AE = 12 cm.
∴ BD = AB - AD = (12 – 8) cm = 4 cm.
CE = AC – AE = (18 12) cm = 6 cm.
.
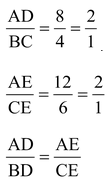Thus, DE divides sides AB and AC of ΔABC in the same ratio. Therefore, by the converse of basic proportionality theorem we have DE||BC.
Question 3.
In a trapezium ABCD AB||DC and DC = 2AB. EF drawn parallel to AB cuts AD in F and BC in E such that
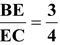. Diagonal DB intersects EF at G. Prove that 7FE = 10AB.
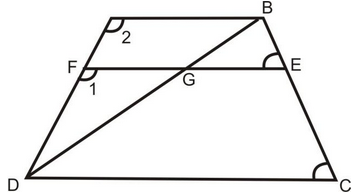
Solution:
In ΔDFG and ΔDAB,
∠1 = ∠2 [Corresponding ∠s ∴ AB || FG]
∠FDG = ∠ADB [Common]
∴ ΔDFG ~ ΔDAB [By AA rule of similarity]
From (i) and (ii), we get
FG/AB = 4/7 i.e. FG = 4/7 AB ......(iii)
In ΔBEG and ΔBCD, we have
∠BEG = ∠BCD [Corresponding angle ∴ EG||CD]
∠GBE = ∠DBC [Common]
∴ ΔBEG ~ ΔBCD [By AA rule of similarity]
Hence proved.
Question
4. In ΔABC, if AD is the bisector of ∠A, prove that
.
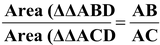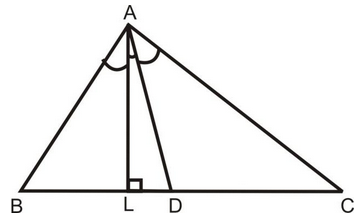
Solution:
In ΔABC, AD is the bisector of ∠A.
∴ AB/AC = BD/DC....(i) [By internal bisector theorem]
From A draw AL⊥BC
.
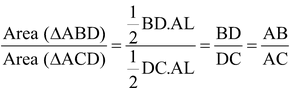[From (i)] Hence Proved.
Question 5.
∠BAC = 90o, AD is its bisector. IF DE⊥ AC, prove that DE × (AB + AB) = AB × AC.
Solution:
It is given that AD is the bisector of ∠A of ΔABC.
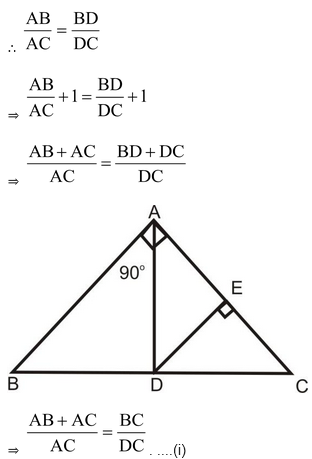
In Δ’s CDE and CBA, we have
∠DCE = ∠BCA [Common]
∠DEC = ∠BAC. [Each equal to 90o]
So by AA-criterion of similarity
Δ CDE ~ Δ CBA
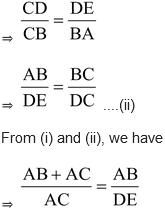
⇒ DE × (AB + AC) = AB × AC.
Question 6.
In the given figure, PA, QB and RC are each perpendicular to AC. Prove that
.
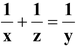Solution:
In ΔPAC, we have BQ||AP
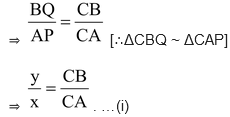
In ΔACR, we have BQ||CR
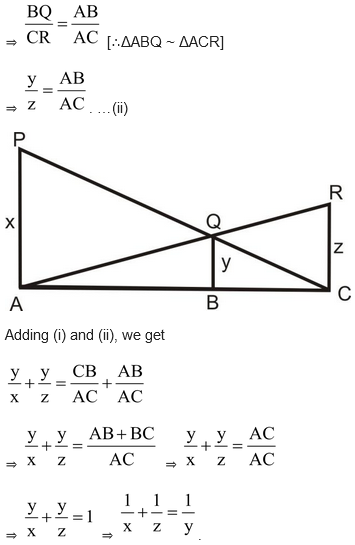
Hence Proved
Question 7.
In the given figure, AB||CD. Find the value of x.
Solution:
Since the diagonals of a trapezium divide each other proportionally.
∴
⇒
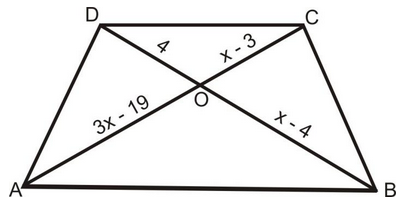
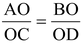
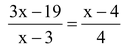
⇒ 12x – 76 = x
2
– 4x – 3x + 12
⇒ x
2
– 19x + 88 = 0
⇒ x
2
– 11x – 8x + 88 = 0
⇒ (x – 8) (x – 11) = 0
⇒ x = 8 or x = 11.
CRITERIA FOR SIMILARITY OF TWO TRIANGLES
Two triangles are said to be similar if (i) their corresponding angles are equal and (ii) their corresponding sides are in the same ratio (or proportional).
Thus, two triangles ABC and A'B'C' are similar if
(i)
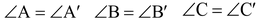and
(ii)
.
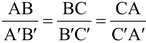In this section, we shall make use of the theorems discussed in earlier sections to derive some criteria for similar triangles which in turn will imply that either of the above two conditions can be used to define the similarity of two triangles.
