
NCERT Solutions for Class 8 Maths Chapter 4: NCERT Solutions for Class 8 Maths Chapter 4, "Practical Geometry," teach students how to draw geometric shapes accurately using tools like a compass, ruler, and protractor.
This chapter covers essential skills such as constructing line segments, angles, triangles, and other figures step by step. The solutions provide clear instructions and diagrams to help students understand each construction easily. By practicing these exercises, students not only improve their geometry skills but also develop their ability to solve problems and think spatially. These solutions are helpful for exam preparation and building a solid understanding of practical geometry.NCERT Solutions for Class 8 Maths Chapter 4 Overview
These solutions for NCERT Class 8 Maths Chapter 4, "Practical Geometry," are prepared by subject experts of Physics Wallah. The solutions include step-by-step instructions and diagrams to help students understand and practice constructing line segments, angles, triangles, and other geometric shapes.NCERT Solutions for Class 8 Maths Chapter 4 PDF
Here is the PDF link for NCERT Solutions for Class 8 Maths Chapter 4, "Practical Geometry." These solutions cover the basics of geometric constructions using tools like a compass and ruler. They provide step-by-step instructions and diagrams to help students learn how to construct line segments, angles, triangles, and other shapes accurately. This PDF is a valuable resource for students to enhance their understanding of practical geometry, prepare for exams, and build confidence in solving geometric problems effectively.NCERT Solutions for Class 8 Maths Chapter 4 PDF
NCERT Solutions For Class 8 Maths Chapter 4 Practical Geometry
Here we have provided NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry for the ease of students so that they can prepare better for their exams.NCERT Solutions For Class 8 Maths Chapter 4 Practical Geometry Exercise 4.1 Page: 60
1. Construct the following quadrilaterals.(i) Quadrilateral ABCD AB = 4.5 cm
BC = 5.5 cm
CD = 4 cm AD = 6 cm AC = 7 cm
Solution: The rough sketch of the quadrilateral ABCD can be drawn as follows.
(1) ∆ABC can be constructed by using the given measurements as follows.
The rough sketch of the quadrilateral ABCD can be drawn as follows.
(1) ∆ABC can be constructed by using the given measurements as follows.
 (2) Vertex D is 6 cm away from vertex A. Therefore, while taking A as the centre, draw an arc of radius 6 cm.
(2) Vertex D is 6 cm away from vertex A. Therefore, while taking A as the centre, draw an arc of radius 6 cm.
 (3) Taking C as the centre, draw an arc of radius 4 cm, cutting the previous arc at point D. Joint D to A and C.
(3) Taking C as the centre, draw an arc of radius 4 cm, cutting the previous arc at point D. Joint D to A and C.
 ABCD is the required quadrilateral.
(ii) Quadrilateral JUMP JU = 3.5 cm
ABCD is the required quadrilateral.
(ii) Quadrilateral JUMP JU = 3.5 cm
UM = 4 cm MP = 5 cm PJ = 4.5 cm PU = 6.5 cm
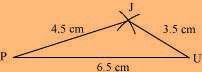
Solution: The rough sketch of the quadrilateral JUMP can be drawn as follows.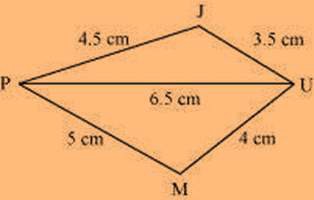 (1) ∆ JUP can be constructed by using the given measurements as follows.
(1) ∆ JUP can be constructed by using the given measurements as follows.
 (2) Vertex M is 5 cm away from vertex P and 4 cm away from vertex U. Taking P and U as centres, draw arcs of radii 5 cm and 4 cm, respectively. Let the point of intersection be M.
(2) Vertex M is 5 cm away from vertex P and 4 cm away from vertex U. Taking P and U as centres, draw arcs of radii 5 cm and 4 cm, respectively. Let the point of intersection be M.
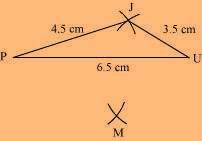 (3) Join M to P and U.
(3) Join M to P and U.
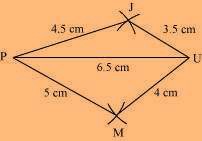 JUMP is the required quadrilateral.
JUMP is the required quadrilateral.
(iii) Parallelogram MORE
OR = 6 cm
Solution:RE = 4.5 cm
EO = 7.5
We know that opposite sides of a parallelogram are equal in length, and also, these are parallel to each other. i.e., ME = OR, MO = ER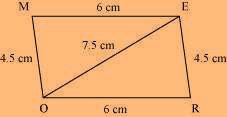 The rough sketch of the parallelogram MORE can be drawn as follows.
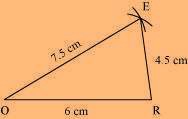
(1) ∆ EOR can be constructed by using the given measurements as follows.
The rough sketch of the parallelogram MORE can be drawn as follows.
(1) ∆ EOR can be constructed by using the given measurements as follows.
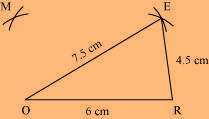
 (2) Vertex M is 4.5 cm away from vertex O and 6 cm away from vertex E. Therefore, while taking O and E as centres, draw arcs of 4.5 cm radius and 6 cm radius, respectively. These will intersect each other at point M.
(2) Vertex M is 4.5 cm away from vertex O and 6 cm away from vertex E. Therefore, while taking O and E as centres, draw arcs of 4.5 cm radius and 6 cm radius, respectively. These will intersect each other at point M.
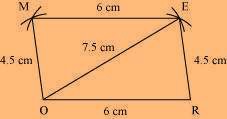
 (3) Join M to O and E.
(3) Join M to O and E.
 MORE is the required parallelogram.
MORE is the required parallelogram.
(iv) Rhombus BEST
BE = 4.5 cm
ET = 6 cm
Solution: We know that all sides of a rhombus are of the same measure. Hence, BE = ES = ST = TB The rough sketch of the rhombus BEST can be drawn as follows.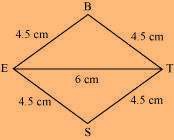
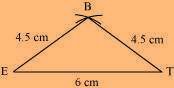 (
1) ∆ BET can be constructed by using the given measurements as follows.
(2) Vertex S is 4.5 cm away from vertex E and also from vertex T. Therefore, while taking E and T as centres, draw arcs of 4.5 cm radius, which will intersect each other at point S.
(
1) ∆ BET can be constructed by using the given measurements as follows.
(2) Vertex S is 4.5 cm away from vertex E and also from vertex T. Therefore, while taking E and T as centres, draw arcs of 4.5 cm radius, which will intersect each other at point S.
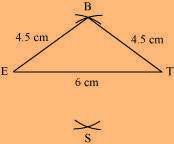 (3) Join S to E and T.
(3) Join S to E and T.
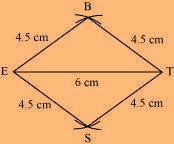
NCERT Solutions For Class 8 Maths Chapter 4 Practical Geometry Exercise 4.2 Page: 62
1. Construct the following quadrilaterals.
(i) Quadrilateral LIFT LI = 4 cm
IF = 3 cm TL = 2.5 cm LF = 4.5 cm
IT = 4 cm
Solution: A rough sketch of the quadrilateral LIFT can be drawn as follows.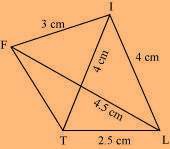 (1) ∆ ITL can be constructed by using the given measurements as follows.
(1) ∆ ITL can be constructed by using the given measurements as follows.
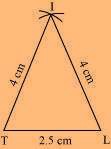 (2) Vertex F is 4.5 cm away from vertex L and 3 cm away from vertex I. ∴ while taking L and I as centres, draw arcs of 4.5 cm radius and 3 cm radius, respectively, which will intersect each other at point F.
(2) Vertex F is 4.5 cm away from vertex L and 3 cm away from vertex I. ∴ while taking L and I as centres, draw arcs of 4.5 cm radius and 3 cm radius, respectively, which will intersect each other at point F.
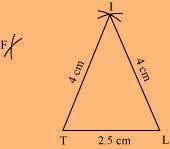
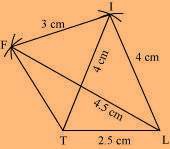 (3) Join F to T and F to I.
LIFT is the required quadrilateral.
(ii) Quadrilateral GOLD OL = 7.5 cm
(3) Join F to T and F to I.
LIFT is the required quadrilateral.
(ii) Quadrilateral GOLD OL = 7.5 cm
GL = 6 cm GD = 6 cm LD = 5 cm OD = 10 cm
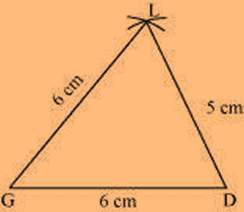
Solution: The rough sketch of the quadrilateral GOLD can be drawn as follows.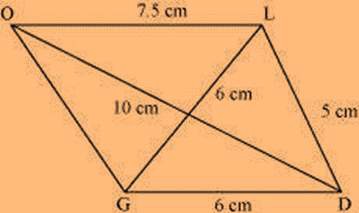 (1) ∆ GDL can be constructed by using the given measurements as follows.
(1) ∆ GDL can be constructed by using the given measurements as follows.
 (2) Vertex O is 10 cm away from vertex D and 7.5 cm away from vertex L. Therefore, while taking D and L as centres, draw arcs of 10 cm radius and 7.5 cm radius, respectively. These will intersect each other at point O.
(2) Vertex O is 10 cm away from vertex D and 7.5 cm away from vertex L. Therefore, while taking D and L as centres, draw arcs of 10 cm radius and 7.5 cm radius, respectively. These will intersect each other at point O.
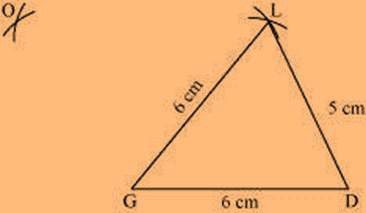 (3) Join O to G and L.
(3) Join O to G and L.
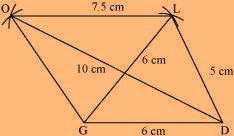 GOLD is the required quadrilateral.
GOLD is the required quadrilateral.
(iii) Rhombus BEND
BN = 5.6 cm
DE = 6.5 cm
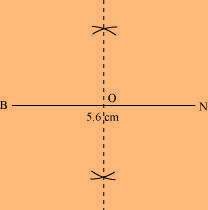
Solution: We know that the diagonals of a rhombus always bisect each other at 90º. Let us assume that these are intersecting each other at point O in this rhombus. Hence, EO = OD = 3.25 cm The rough sketch of the rhombus BEND can be drawn as follows.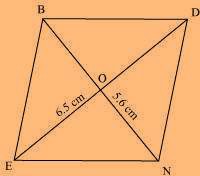 (1) Draw a line segment BN of 5.6 cm, and also draw its perpendicular bisector. Let it intersect the line segment BN at point O.
(1) Draw a line segment BN of 5.6 cm, and also draw its perpendicular bisector. Let it intersect the line segment BN at point O.
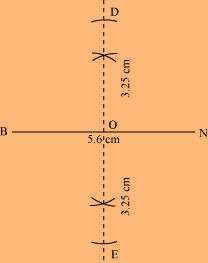
 (2) Taking O as the centre, draw arcs of 3.25 cm radius to intersect the perpendicular bisector at points D and E.
(2) Taking O as the centre, draw arcs of 3.25 cm radius to intersect the perpendicular bisector at points D and E.
 (3) Join points D and E to points B and N.
(3) Join points D and E to points B and N.
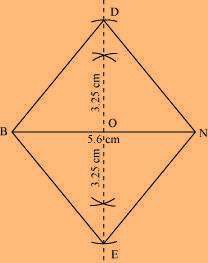 BEND is the required quadrilateral.
BEND is the required quadrilateral.
NCERT Solutions For Class 8 Maths Chapter 4 Practical Geometry Exercise 4.3 Page: 64
1. Construct the following quadrilaterals.
(i) Quadrilateral MORE MO = 6 cm
OR = 4.5 cm
∠M = 60°
∠O = 105°
∠R = 105°
Solution: Rough Figure:
 (1) Draw a line segment MO of 6 cm and an angle of 105º at point O. As vertex R is 4.5 cm away from the vertex O, cut a line segment OR of 4.5 cm from this ray.
(2) Again, draw an angle of 105º at point R.
(1) Draw a line segment MO of 6 cm and an angle of 105º at point O. As vertex R is 4.5 cm away from the vertex O, cut a line segment OR of 4.5 cm from this ray.
(2) Again, draw an angle of 105º at point R.
 (3) Draw an angle of 60º at point M. Let this ray meet the previously drawn ray from R at point E.
(3) Draw an angle of 60º at point M. Let this ray meet the previously drawn ray from R at point E.
 MORE is the required quadrilateral.
(ii) Quadrilateral PLAN PL = 4 cm
MORE is the required quadrilateral.
(ii) Quadrilateral PLAN PL = 4 cm
LA = 6.5 cm
∠P = 90°
∠A = 110°
∠N = 85°
Solution: The sum of the angles of a quadrilateral is 360°. In quadrilateral PLAN, ∠P + ∠L + ∠A + ∠N = 360° 90° + ∠L + 110° + 85° = 360° 285° + ∠L = 360° ∠L = 360° − 285° = 75° Rough Figure: (1) Draw a line segment PL of 4 cm and draw an angle of 75º at point L. As vertex A is 6.5 cm away from vertex L, cut a line segment LA of 6.5 cm from this ray.
(1) Draw a line segment PL of 4 cm and draw an angle of 75º at point L. As vertex A is 6.5 cm away from vertex L, cut a line segment LA of 6.5 cm from this ray.
 (2) Again, draw an angle of 110º at point A.
(2) Again, draw an angle of 110º at point A.
 (3) Draw an angle of 90º at point P. This ray will meet the previously drawn ray from A at point N.
(3) Draw an angle of 90º at point P. This ray will meet the previously drawn ray from A at point N.
 PLAN is the required quadrilateral.
PLAN is the required quadrilateral.
(iii) Parallelogram HEAR HE = 5 cm
EA = 6 cm
∠R = 85°
Solution: Rough Figure: (1) Draw a line segment HE of 5 cm and an angle of 85º at point E. As vertex A is 6 cm away from vertex E, cut a line segment EA of 6 cm from this ray.
(1) Draw a line segment HE of 5 cm and an angle of 85º at point E. As vertex A is 6 cm away from vertex E, cut a line segment EA of 6 cm from this ray.
 (2) Vertex R is 6 cm and 5 cm away from vertex H and A, respectively. By taking radii as 6 cm and 5 cm, draw arcs from points H and A, respectively. These will intersect each other at point R.
(2) Vertex R is 6 cm and 5 cm away from vertex H and A, respectively. By taking radii as 6 cm and 5 cm, draw arcs from points H and A, respectively. These will intersect each other at point R.
 (3) Join R to H and A.
(3) Join R to H and A.
 HEAR is the required quadrilateral.
HEAR is the required quadrilateral.
(iv) Rectangle OKAY
OK = 7 cm KA = 5 cm
Solution: Rough Figure: (1) Draw a line segment OK of 7 cm and an angle of 90º at point K. As vertex A is 5 cm away from vertex K, cut a line segment KA of 5 cm from this ray.
(1) Draw a line segment OK of 7 cm and an angle of 90º at point K. As vertex A is 5 cm away from vertex K, cut a line segment KA of 5 cm from this ray.
 (2) Vertex Y is 5 cm and 7 cm away from vertex O and A, respectively. By taking
radii as 5 cm and 7 cm, draw arcs from points O and A, respectively. These will intersect each other at point Y.
(2) Vertex Y is 5 cm and 7 cm away from vertex O and A, respectively. By taking
radii as 5 cm and 7 cm, draw arcs from points O and A, respectively. These will intersect each other at point Y.
 (3) Join Y to A and O.
(3) Join Y to A and O.
 OKAY is the required quadrilateral.
OKAY is the required quadrilateral.
NCERT Solutions For Class 8 Maths Chapter 4 Practical Geometry Exercise 4.4 Page: 67
1. Construct the following quadrilaterals,(i) Quadrilateral DEAR DE = 4 cm
EA = 5 cm AR
= 4.5 cm
∠E = 60°
∠A = 90°
Solution: Rough Figure: (1) Draw a line segment DE of 4 cm and an angle of 60º at point E. As vertex A is 5 cm away from vertex E, cut a line segment EA of 5 cm from this ray.
(1) Draw a line segment DE of 4 cm and an angle of 60º at point E. As vertex A is 5 cm away from vertex E, cut a line segment EA of 5 cm from this ray.
 (2) Again, draw an angle of 90º at point A. As vertex R is 4.5 cm away from vertex A, cut a line segment RA of 4.5 cm from this ray.
(2) Again, draw an angle of 90º at point A. As vertex R is 4.5 cm away from vertex A, cut a line segment RA of 4.5 cm from this ray.

 (3) Join D to R.
DEAR is the required quadrilateral.
(3) Join D to R.
DEAR is the required quadrilateral.
(ii) Quadrilateral TRUE TR = 3.5 cm
RU = 3 cm UE = 4 cm
∠R = 75°
∠U = 120°
Solution: Rough Figure: (1) Draw a line segment RU of 3 cm and an angle of 120º at point U. As vertex E is 4 cm away from vertex U, cut a line segment UE of 4 cm from this ray.
(1) Draw a line segment RU of 3 cm and an angle of 120º at point U. As vertex E is 4 cm away from vertex U, cut a line segment UE of 4 cm from this ray.
 (2) Next, draw an angle of 75º at point R. As vertex T is 3.5 cm away from vertex R, cut a line segment RT of 3.5 cm from this ray.
(2) Next, draw an angle of 75º at point R. As vertex T is 3.5 cm away from vertex R, cut a line segment RT of 3.5 cm from this ray.
 (3) Join T to E.
(3) Join T to E.
 TRUE is the required quadrilateral.
TRUE is the required quadrilateral.
NCERT Solutions For Class 8 Maths Chapter 4 Practical Geometry Exercise 4.5 Page: 68
Draw the following:1. The square READ with RE = 5.1 cm
Solution: All the sides of a square are of the same measure, and also, all the interior angles of a square are 90º measure. Therefore, the given square READ can be drawn as follows. Rough Figure:
(1) Draw a line segment RE of 5.1 cm and an angle of 90º at points R and E.
Rough Figure:
(1) Draw a line segment RE of 5.1 cm and an angle of 90º at points R and E.
 (2) As vertex A and D are 5.1 cm away from vertex E and R, respectively, cut line segments EA and RD, each of 5.1 cm from these rays.
(2) As vertex A and D are 5.1 cm away from vertex E and R, respectively, cut line segments EA and RD, each of 5.1 cm from these rays.
 (3) Join D to A.
(3) Join D to A.
 READ is the required square.
READ is the required square.
2. A rhombus whose diagonals are 5.2 cm and 6.4 cm long. Solution:
In a rhombus, diagonals bisect each other at 90º. ∴, the given rhombus ABCD can be drawn as follows.
 Rough Figure:
(1) Draw a line segment AC of 5.2 cm and draw its perpendicular bisector. Let it intersect the line segment AC at point O.
Rough Figure:
(1) Draw a line segment AC of 5.2 cm and draw its perpendicular bisector. Let it intersect the line segment AC at point O.
 (2) Draw arcs of 6.4/2 = 3.2 on both sides of this perpendicular bisector. Let the arcs intersect the perpendicular bisector at points B and D.
(2) Draw arcs of 6.4/2 = 3.2 on both sides of this perpendicular bisector. Let the arcs intersect the perpendicular bisector at points B and D.
 (3) Join points B and D with points A and C.
(3) Join points B and D with points A and C.
 ABCD is the required rhombus.
ABCD is the required rhombus.
3. A rectangle with adjacent sides of length 5 cm and 4 cm. Solution:
Opposite sides of a rectangle have lengths of the same measure, and also, all the interior angles of a rectangle are 90º measure. The given rectangle ABCD may be drawn as follows.
Rough figure: (1) Draw a line segment AB of 5 cm and an angle of 90º at points A and B.
(1) Draw a line segment AB of 5 cm and an angle of 90º at points A and B.
 (2) As vertex C and D are 4 cm away from vertex B and A, respectively, cut line segments AD and BC, each of 4 cm, from these rays.
(2) As vertex C and D are 4 cm away from vertex B and A, respectively, cut line segments AD and BC, each of 4 cm, from these rays.
 (3) Join D to C.
(3) Join D to C.
 ABCD is the required rectangle.
ABCD is the required rectangle.
4. A parallelogram OKAY where OK = 5.5 cm and KA = 4.2 cm. Solution:
Opposite sides of a parallelogram are equal and parallel to each other. The given parallelogram OKAY can be drawn as follows. Rough Figure: (1) Draw a line segment OK of 5.5 cm and a ray at point K at a convenient angle.
(1) Draw a line segment OK of 5.5 cm and a ray at point K at a convenient angle.
 (2) Draw a ray at point O parallel to the ray at K. As the vertices A and Y are 4.2 cm away from the vertices K and O, respectively, cut line segments KA and OY, each of 4.2 cm, from these rays.
(2) Draw a ray at point O parallel to the ray at K. As the vertices A and Y are 4.2 cm away from the vertices K and O, respectively, cut line segments KA and OY, each of 4.2 cm, from these rays.
 (3) Join Y to A.
(3) Join Y to A.
 OKAY is the required rectangle.
OKAY is the required rectangle.
Benefits of NCERT Solutions For Class 8 Maths Chapter 4
- Clear Guidance : The solutions provide clear and concise explanations on how to perform geometric constructions using a compass and ruler, helping students understand the concepts easily.
- Step-by-Step Instructions : Each solution provides step-by-step instructions and diagrams for constructing various geometric shapes such as line segments, angles, triangles, and quadrilaterals, making learning practical geometry straightforward.
- Skill Development : By practicing these constructions, students develop important skills in geometry, such as spatial reasoning, measurement accuracy, and problem-solving abilities.
- Exam Preparation : These solutions are aligned with the NCERT curriculum and help students prepare effectively for exams by covering all important topics and providing ample practice exercises.
- Enhanced Understanding : The solutions reinforce understanding of geometric principles and concepts, ensuring students have a solid foundation in practical geometry.
- Self-Study Resource : Students can use these solutions for self-study, allowing them to learn at their own pace and revise concepts as needed.
NCERT Solutions for Class 8 Maths Chapter 4 FAQs
What is Practical Geometry?
What are the basic tools used in Practical Geometry?
Why is learning Practical Geometry important?
How do I construct different geometric shapes?









