
Compound interest formula
Commercial Mathematics of Class 8
Compound interest is the interest charged on the loan or deposit amount. It is the most commonly used concept in our daily life. The compound interest for a certain amount depends on the principal and the interest earned over the period. This is the main difference between simple interest and compound interest.
Suppose we follow our bank statements; we usually notice that some interest is credited to our account every year. This interest varies each year for the same principal amount. We see interest growing in the coming years. So we can include that the interest charged by the bank is not simple interest; this interest is called compound interest or CI. In this short article, you will go through what CI is, the formula, and the derivation of the formula to calculate CI when compounded annually, semi-annually, quarterly, etc. Also, one can understand why the return on compound interest is greater than the return on simple interest. The examples mentioned here are based on real CI applications.
Compound Interest Definition
Compound interest is interest calculated from the principal and interest accumulated over the previous period. It differs from simple interest, where the interest is not added to the principal when calculating the interest in the next period. In mathematics, compound interest is usually referred to as C.I.
Compound interest is used in most transactions in the banking and financial sector and other areas. Some of its applications are:
- Increase or decrease in population.
- Bacteria growth.
- Growth or depreciation of the value of the item
Compound Interest Formula
As we have already discussed, compound interest is interest based on the initial amount of principal and interest collected over a period of time. The compound interest formula is given below:
A = P+(1+r/n) nt
Where,
A = amount
P = principal
r = rate of interest
n = number of times interest is compounded per year
t = time (in years)
Also, we can write the formula as given below:
CI = A – P
And
CI = P(1+r/n) nt - P
Where,
A = New principal sum or the total amount of money after the compounding period
P = Original amount or initial amount
r = Annual interest rate
n = Compounding frequency or the number of times interest is compounded in a year
t = the number of years
If the interest is compounded annually, the amount is given as:
A = P(1+R/100) t
Therefore, the compound interest rate formula can be expressed for different scenarios such as the interest rate is compounded yearly, half-yearly, quarterly, monthly, daily, etc.
Interest Compounded for Different Years
| Time (in years) | Amount | Interest |
| 1 | P(1+R/100) | PR/100 |
| 2 | P(1+R/100) 2 | P(1+R/100) 2 -P |
| 3 | P(1+R/100) 3 | P(1+R/100) 3 -P |
| 4 | P(1+R/100) 4 | P(1+R/100) 4 -P |
| n | P(1+R/100) n | P(1+R/100) n -P |
Derivation of Compound Interest Formula
To derive the compound interest formula, we will use the simple interest formula as we already know SI for 1 year is equal to CI for 1 year (when compounded annually).
Let, P = Compound Interest Formula
n = Time
R = Years Rate
Simple Interest (SI) for the first year:
SI1 = P x R x T / 100
Amount after first year = P + SI 1
= P = P x R x T / 100
= P(1+ R/100)
= P(1+ R/100)
= P 2
Simple Interest (SI) for second year:
SI 2 = P 2 x R x T / 100
Amount after second year =
P 2 + SI 2
= P 2 + P 2 x R x T / 100
= P 2 (1+ R/100)
= P(1+ R/100) (1+ R/100)
= P(1+ R/100) 2
Alternatively, if we proceed further to n years, we can deduce:
A = P(1+ R/100) n
CI = A - P
= P[(1+ R/100) n - 1]
Compound Interest Formula- Half Yearly
In the case of compound interest, the interest varies according to the calculation period. If the interest calculation period is half-yearly, the interest is calculated every six months, and the amount is added twice a year.
The formula for calculating compound interest when the principal is compounded semi-annually or half-yearly is given as follows:
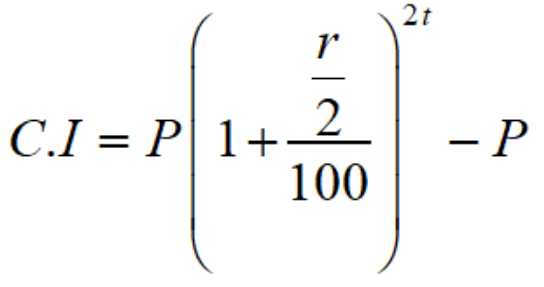
Here, compound interest is calculated over a half-yearly period; thus, the interest rate r is divided by 2, and the time is doubled. The formula for calculating the amount when the principal is compounded semi-annually or half-yearly is given as follows:
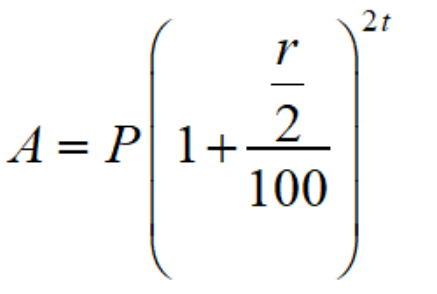
Where,
A is the amount at the end of the time period
P is the initial principal value, and r is the rate of interest per annum
t is the time period
C.I. is the compound interest.
Compound Interest Formula- Quarterly
If the time period for calculating the interest is quarterly, the interest is calculated every three months, and the amount is added up 4 times a year. The formula for calculating compound interest when the principal is compounded quarterly is given as follows:
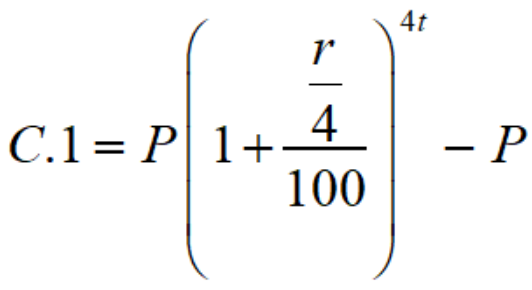
Here, compound interest is calculated over a quarterly time period; thus, the interest rate r is divided by 4, and the time is increased by 4. The formula for calculating the amount in the quarterly principal sum is given as follows:
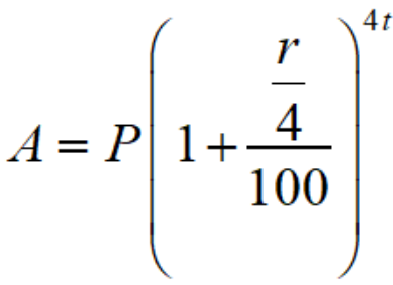
Where,
A is the amount at the end of the time period
P is the initial principal value, and r is the rate of interest per annum
t is the time period
C.I. is the compound interest.
How to Calculate Compound Interest
You can calculate compound interest using a simple formula. It is calculated by multiplying the first principal amount by one and adding the increased annual interest rate to the number of compound periods by subtracting by one. The total initial amount of your loan is then deducted from the resulting value.
Compound Interest Examples
Q1. A small town had 20,000 residents in 4000. Its population declines at a rate of 20% per annum. What will be its total population in 2006?
Ans. The population of the town decreases by 20% every year. Therefore, it has a new population every year. Now, the population for the next year is calculated on the current year population. For the decrease, we have the formula A = P(1 – R/100) n
Therefore, the population at the end of 6 years = 20000(1 – 10/100) 6
= 20000(1 – 0.1) 6 = 20000 x 0.956 = 11,101.2
Q2. The price of a T.v is Rs. 1500 and it depreciates by 10% per month. Find its value after 4 months.
Ans. For the depreciation, we have the formula A = P(1 – R/100) n .
Thus, the price of the radio after 4 months = 1500(1 – 10/100) 4
= 1500(1 – 0.1) 4 = 1500(0.9) 4 = Rs. 984.15
Frequently Asked Question (FAQs)
Q1. How to calculate interest rate?
Ans. It is the percentage of the principal amount that the lender or bank charges the borrower for using its money or assets for a specific time. The interest rate formula is Interest Rate = (Simple Interest × 100)/(Principal × Time).
Q2. What is the formula of compound interest?
Ans. The compound interest formula is given below:
CI = Amount – Principal
Where,
A = P+(1+r/n)nt
P = Principal
A = Amount
r = Annual interest rate
n = Number of compounding periods
t = Time (in years)
Q3. Who benefits from compound interest?
Ans. The investors get benefit from the (C.I) compound interest since the interesting pair here on principle plus on the interest which they have already earned.







