Percentage

The term "percentage" was taken from the Latin word "per centum," meaning "hundred." Percents are fractions with 100 as the denominator. In other words, it is a relationship between the whole and the part, where the value of the whole or part is always taken as 100.

What is the Percentage?

A percentage is a ratio or fraction in which the value of the whole is always 100. For example, if ram scored 40% on his English test, that means he scored 40 out of 100. It is written as 40/100 in fraction form, and the ratio is 40:100.

Percentage Formula

To calculate the percentage, we have to divide the value by the total value and then multiply the resultant by 100.

Formula = (Value/Total value) × 100

Example: 3/5 × 100 = 0.6 × 100 = 60 per cent

How to calculate the percentage of a number?

To calculate the percentage of a number, then, we will use a different formula such as:

A% of Number = X

whereas X is the percentage.

If the % sign is removed, then we need to express the formula given above

A/100 * Number = X

Example: Calculate 10% of 80.

Let 10% of 80 = X

10/100 * 80 = X

X = 8

How to Calculate Percentage Increase?

Percentage increase refers to the change in value in an exchange rate as it increases over a period of time. For example, an increase in population, an increase in the number of bacteria on a surface, etc. The percentage increase can be calculated using the following formula:

Percentage increase = (increase value - original value)/original value × 100

How to Calculate Percentage Decrease?

Percentage decrease refers to the change in value in an exchange rate when it decreases over a period of time. For example, a decrease in rainfall levels, a decrease in the number of Covid patients, etc. The percentage decrease can be calculated using the following formula:

Percent decrease = (Original Value-decrease Value)/Original Value × 100

Percentage Difference Formula

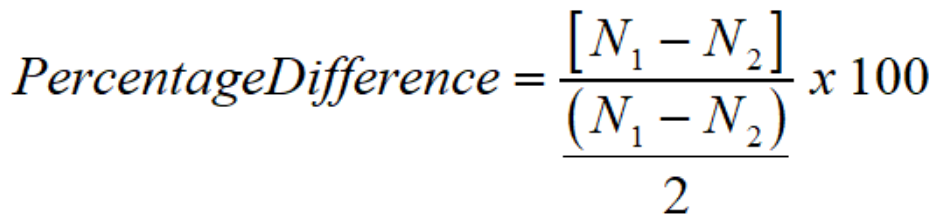
Percentage Formula Examples

Q1. Find the number if 14% of 30% of a number is 6.

Ans. Let X be the required number.

Therefore, as per the given question,

(14/100) × (30/100) × X = 6

So, X = (6 × 100 × 100) / (14 × 30)

= 142.8

Q2. What percentage of 1/7 is 1/35?

Ans. Let X% of 1/7 be 1/35.

[(1/7) / 100] × X = 1/35

X = (1/35) × (7/1) × 100

X = 20%

Q3. Which number is 40% less than 90?

Ans. Required number = 60% of 90

= (90 x 60)/100

= 54

Q4. A fruit seller had some apples. He sells 60% apples and still has 520 apples. Originally, he had how many apples?

Ans. Let he had N apples, originally.

Now, as per the given question, we have;

(100 – 60)% of N = 520

⇒ (40/100) × N = 520

⇒ N = (520 × 100/40) = 1300

Frequently Asked Question (FAQs)

Q1. How to find percentage?

Ans.The percentage can be calculated by dividing the value by the total value and multiplying the final value by 100. The formula to find the percentage is (value/total value)×100%.

Q2. How do you find an unknown percentage?

Ans. To find out what percentage the first number is of the second number, a shortcut is to simply divide the first number (the numerator) by the second number (the denominator). The result will be a decimal number that can be converted to a percentage.

Q3. Are all percentages reversible?

Ans. Arithmetic multiplication is commutative. Therefore, values in a percentage calculation are reversible.