Electric Current

Flow of electric charge constitutes electric current. For a given conductor AB, if 'δQ' charge flows through a cross-section of area A in time 'δt', then the electric current through the conductor AB, is given as

I = δQ/δt 

The current so defined above, is the average current over the period δt. The instantaneous current is given as I = dQ/dt

Direction of electric current as defined above will be taken along the direction of flow of positive charge (although in majority of conductors the charge carrier is electron which is negatively charged and hence electric current would be in a direction opposite to that of flow of electrons).

Despite the direction that we associate with electric current, it is not a vector quantity. Instead, we choose current density (j), that is current flowing through unit area of the cross−section, as a vector quantity.

Unit of Electric Current

The SI unit of electric current is ampere. It is denoted by A.

1 ampere (A)  = 1 coulomb / second

Current Density (J)

To describe the flow of charge through a cross section of the conductor at a particular point, we use the term current density J. The direction of flow of positive charge is same as that of the direction of the electric field E, and the direction of flow of –ve charge is opposite to the direction of the electric field. The direction of current density J is same as that of the electric field.

For each element of cross−section, the magnitude of current density J is equal to the current per unit area through that element.

The total current through the conductor is given as

i = 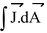. . . (i)

where dA is the area vector of the element, perpendicular to it

If the current is uniform across the surface and parallel to dA, then current density J is also uniform and parallel to area vector dA. Hence, from equation (i)

i = 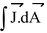= JA

or J = i/A

where A is the total cross−sectional area of the surface. S.I. unit for current density is the ampere per square meter (A/m²).

Illustration 1. How many electrons pass through a wire in 1 minute if the current passing through the wire is 200 mA ?

Solution: I = q/t = ne/t

or, n = It/e

or, n = 200 x 10^-3 x 60/1.6 x 10^-19 = 7.5 × 10^19.

Illustration 2. One billion electrons pass through a conductor AB from end A to end B in 1 ms. What is the direction and magnitude of current?

Solution : i =  ne/t = (10⁹)(1.6 x 10^-19)/10^-3 = 1.6 × 10^-7 Amp.

⇒ i = 0.16 μ A. The current flows from B to A.

Illustration 3. A particle having charge q coulomb describes a circular orbit. If radius of the orbit is R and frequency of the orbital motion of particle is f, then find the current in the orbit.

Solution: Through any section of the orbit, the charge passes f times in one second. Therefore, through that section total charge passing in one second is fq. By definition i = fq.