Measurement Of Unknown Resistance Using A Post Office Box
Current Electricity of Class 12
MEASUREMENT OF UNKNOWN RESISTANCE USING A POST OFFICE BOX
|
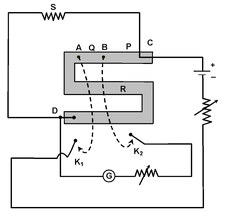
A Post Office Box can also be used to measure an unknown resistance. It is a Wheatstone Bridge with three arms P, Q and R; while the fourth arm is the unknown resistance. P and Q are known as the ratio arms while R is known as the rheostat arm. At balance, the unknown resistance S = (P/Q)R. . . (1) The ratio arms are first adjusted so that they carry 100 Ω each. The resistance in the rheostat arm is now adjusted so that the galvanometer deflection is in one direction. If R = R0 (ohm) and R = R0 + 1 (ohm) are the resistance in rheostat arm, for which the deflection in galvanometer is in opposite direction, then it implies that the unknown resistance ‘S’ lies between R0 & (R0 + 1) ohm. |
|
Now, the resistances in P and Q are made 100 Ω and 1000 Ω, respectively, and the process is repeated.
Equation (1) is used to compute S. The ratio P/Q is progressively made 1:10, and then 1:100. Thus, the resistance S can be accurately measured.
Errors
The major sources of error are the connecting wires, unclear resistance plugs, change in resistance due to Joule heating, and the insensitivity of the Wheatstone bridge.
These errors may be removed by using thick connecting wires, clean plugs, keeping the circuit on for very brief periods (to avoid Joule heating) and calculating the sensitivity.
In order that the sensitivity is maximum, the resistance in the arm P is kept close to the value of the resistance S.
Illustration14. In an experiment with a post−office box, the ratio arms are 1000 : 10. If the value of the third resistance is 999 Ω,. find the unknown resistance.
Solution: The ratio arms are 1000 : 10
∴ P/Q = 1000/10 = 100
Third resistance R = 999 Ω
Let x be the unknown resistance.
We know that,
P/Q = R/X
∴ X = Q/P x R = 1/100 x 999 = 9.99 Ω
Illustration15.When two resistances X and Y are put in the left hand and right hand gaps in a meter bridge, the null point is at 60 cm. If X is shunted by a resistance equal to half of itself then find the shift in the null point.
|
Solution :Arrangement is shown in the figure. X/Y = 60/40 = 3/2 . . (1) When X is shunted, then resistance in the left gap becomes
|
|
Now,
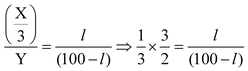
⇒I = 33.3 ∴ Shift = 60 – 33.3 = 26.7 cm
Related Topics

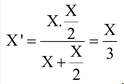 . . . (2)
. . . (2)