Centre Of Mass
Impluse And Momentum of Class 11
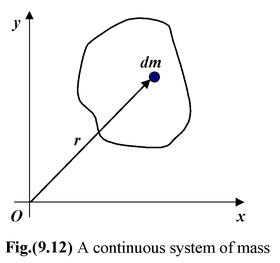
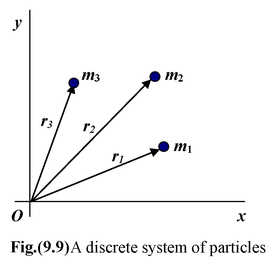
In a system of extended bodies there is one special point that has some interesting and simple properties no matter how complicated the system is. This point is called the center of mass.
|
Definition of Centre of Mass
For a system of n particles whose position vectors are
or
|
|
where M = Σmi is the total mass of the system.
The components of equation (9.18) are defined as
xcm=
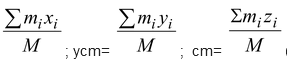 (9.19)
(9.19)
Example 9.9
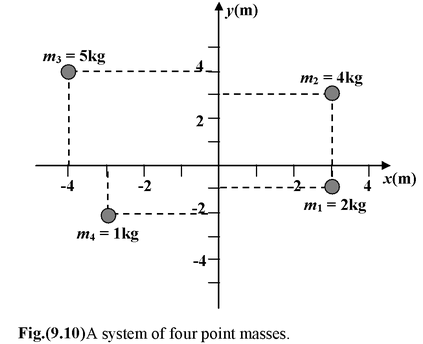
Find the center of mass of the four point masses as shown in figure (9.10).
Solution
The total mass M = 12 kg, from equation (9.19), we have

The position of the cm is
 = -0.42
= -0.42
 + 2.3
+ 2.3
 m
m
Example 9.10
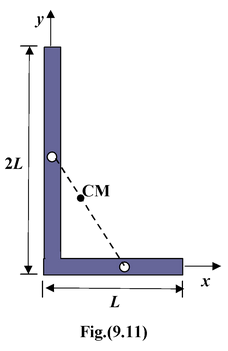
A thin rod of length 3L is bent at right angles at a distance L from one end. Locate the c.m. with respect to the corner. Take L = 1.2 m
|
Solution
The c.m. of each arm is at its midpoint. The c.m. of the two arms can be found by treating each arm as a point particle at its c.m. From the diagram we see that x
1
= L/2, y
1
= 0 and x
2
= 0 , y
2
= L. If we taken
The position of the c.m.is
|
|
|
The center of mass of a continuous body is defined as
The components of this equation are
|
|
Example 9.11
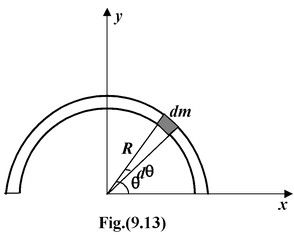
|
Find the center of mass of a semicircular rod of radius R and linear density λ kg/m as shown in the figure. Solution From the symmetry of the body we see that at once that the c.m. must lie along the y axis, so xc.m.= 0. In this case it is convenient to express the mass element in terms of the angle θ, measured in radians. The element, which subtends an angle dθ at the origin, has a length Rdθ and a mass dm = λRdθ. |
|
Here y = Rsinθ. Therefore, y
cm
=
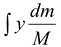 takes the form
takes the form
y
cm
=
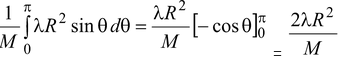
The total mass of the ring is M = πRλ; therefore, ycm= 2R/π
Example 9.12
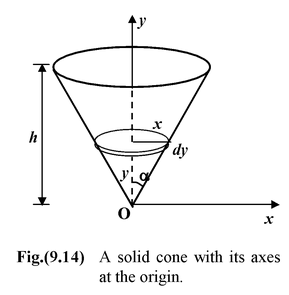
Find the center of mass of a uniform solid cone of height h and semiangle α, as shown in the figure(9.14).
|
Solution
We assume the apex of the cone at the origin. It is clear that the c.m. will lie along the y axis. We divide the cone into disc of radius x and thickness dy. The volume of such a disc is
|
|
M =
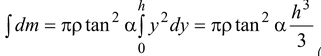 (i)
(i)
The position of the c.m. is given by yc.m.=
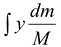
∴yc.m. =
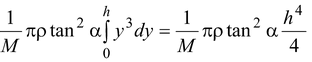 (ii)
(ii)
Using (i) and (ii), we find yc.m. = 3h/4
Motion of the Center of Mass
The instantaneous velocity of the center of mass is given by
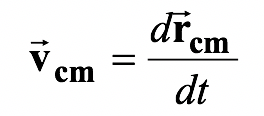
From definition,
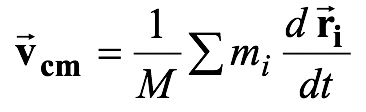
or
![]() =
=
![]() (9.22)
(9.22)
The total momentum of a system of particles is equivalent to that of a single (imaginary) particle of mass M = Σmi moving at the velocity of the center of mass
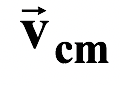 .
.
That is,
![]()
or
![]()
or
![]() (9.23)
(9.23)
Using the concept of center of mass, we may deal with the translational motion of extended objects or systems of particles, as if they were point particle with all the mass concentrated at the center of mass.
Differentiating equation (9.22), with respect to time, we get
![]() =
=
![]()
Since the internal forces cancel in pairs, therefore,
![]()
Thus,
![]() (9.24)
(9.24)
The center of mass accelerates as if it were a point particle of mass M = Σmi and the net external force were applied at this point.
If
![]() = 0, then
= 0, then
![]() = constant (9.25)
= constant (9.25)
If the net external force on a system on particles is zero, the velocity of the center of mass remains constant.
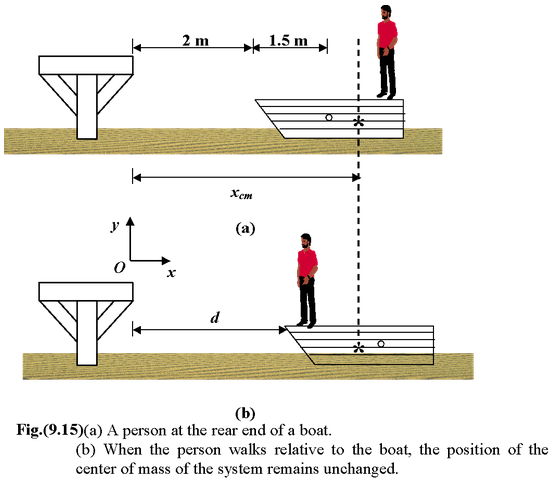
Example 9.13
A man of mass m1= 60 kg is at the rear of a stationary boat of mass m2= 40 kg and length 3 m, which can move freely on the water, as shown in the figure. The front of the boat is
2 m from the dock. What happens when the man walks to the front? Treat the boat as a uniform object.
Solution
The initial position of the c.m. is indicated by a star as shown in the in figure. Since there is no net external force, xc.m.is fixed. We treat the boat as a point particle at its center. In terms of the initial positions,
xc.m.=
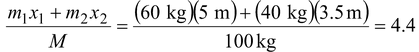 m(i)
m(i)
After the man walks to the front, let us say the front is at a distance d from the dock as shown in figure. In terms of the new positions,
xc.m.=
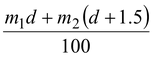 (ii)
(ii)
On equating (i) and (ii) we find d = 3.8 m.
The negative displacement of the man is accompanied by a positive displacement of the boat such that the cm stays fixed. The total momentum of the system remains zero at all times.
Example 9.14
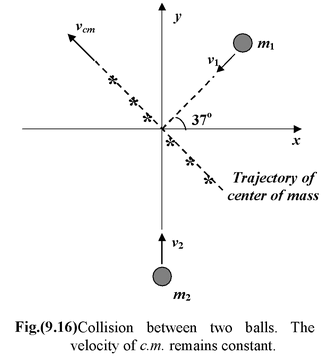
Two balls with masses m1 = 3 kg and m2= 5 kg have initial velocities
v
1
= v
2
= 5 m/s in the directions as shown in the fig.(9.16). They collide at the origin.
(a)Find the velocity of the center of mass 3 s before the collision
(b)Find the position of the center of mass 2 s after the collision
Solution
(a)The given time is of no consequence since vcm is constant for all times.
From equation (9.22), in component form

Thus,
![]() = -1.5
= -1.5
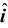 + 2
+ 2
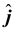 m/s
m/s
(b)Since the collision occurs at the origin, the position of the center of mass 2 s later is
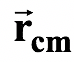 =
=
![]() t = -3
t = -3
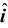 + 4
+ 4
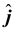 m
m
Example 9.15
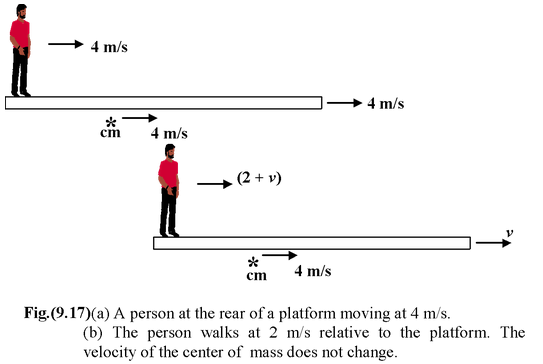
A 75 kg man stands at the rear end of a platform of mass 25 kg and length 4m, which moves initially at 4
 m/s over a frictionless surface. At t = 0, he walks at 2 m/s relative to the platform and then stops at the front end. During the period of walking, find the displacement of
m/s over a frictionless surface. At t = 0, he walks at 2 m/s relative to the platform and then stops at the front end. During the period of walking, find the displacement of
(a) the platform,
(b) the man
(c) the center of mass
Solution
Initially the man, the platform, and the cm have the same velocity, 4
 m/s, as shown in the figure(9.17). When he begins to walk forward, his increase in momentum must be compensated for by a decrease in the platform's momentum. Let us say that the velocity of the platform relative to the ground while he is walking i.e.
m/s, as shown in the figure(9.17). When he begins to walk forward, his increase in momentum must be compensated for by a decrease in the platform's momentum. Let us say that the velocity of the platform relative to the ground while he is walking i.e.
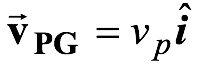
The velocity of man relative to the ground is then
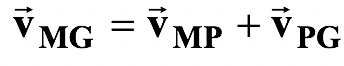 = (2 + vP) 4
= (2 + vP) 4
 .
.
From the conservation of momentum, we have
(75 + 25) × 4 = 75( 2 + vp) + 25 vP
Thus, the velocity of the platform is vP= 2.5 m/s, and
the velocity of the man is vm= 4.5 m/s.
Since the velocity of man relative to platform is 2 m/s,
therefore, it takes
t = 4m/2m/s = 2s
to walk from the rear to the front.
Displacement of platform is
xp= vpt = (2.5)(2) = 5 m
Displacement of the man is
xm= vmt = (4.5)(2) = 9 m
Displacement of the center of mass
x cm = v cm t = (4)(2) = 8 m
The kinetic energy of a system of particles is given by
K = Kcm+ K′(9.26)
where Kcm=
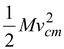 , kinetic energy of the c.m. relative to the fixed origin O.
, kinetic energy of the c.m. relative to the fixed origin O.
andK′ =
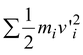 , kinetic energy of the particles relative to the c.m.
, kinetic energy of the particles relative to the c.m.
The term K′ may involve translation, rotation or vibration relative to the center of mass.
Example 9.16
A particle of mass m1 = 4 kg moves at 5
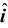 m/s, while m2 = 2 kg moves at 2
m/s, while m2 = 2 kg moves at 2
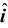 m. Find
m. Find
(a)the kinetic energy of center of mass
(b)the kinetic energy with respect to center of mass.
Solution
The velocity of the cm is obtained by using equation (9.22).
v
cm
=
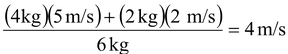
The figure (9.18) shows, the velocities relative to the cm are
v 1 ′ = v 1 - v cm = +1 m/s
v 2 ′ = v 2 – v cm = -2 m/s

The two terms for the total kinetic energy are
(a)Kcm= 1/2(m 1 + m 2 )v cm 2 = 48 J
(b)K′ =
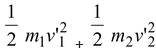 = 6 J
= 6 J

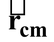 is defined as
is defined as
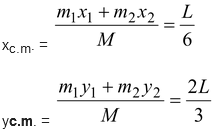
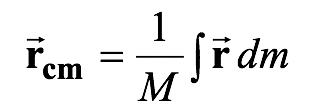 (9.20)
(9.20)
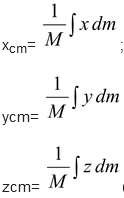 (9.21)
(9.21)