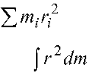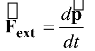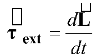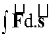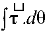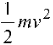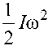Angular Momentum
Rotational Motion of Class 11
|
Consider a particle that has linear momentum
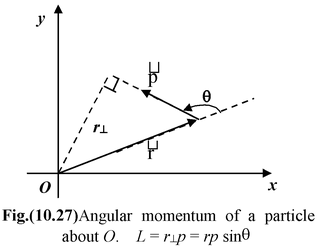
The magnitude of momentum is given by L = rp sinθ or L = r⊥p (10.33) where r⊥ = r sinθ is called the moment arm. |
|
The direction of angular momentum is given by the right hand rule.
The SI unit of angular momentum is kg m2/s.
Example 10.20
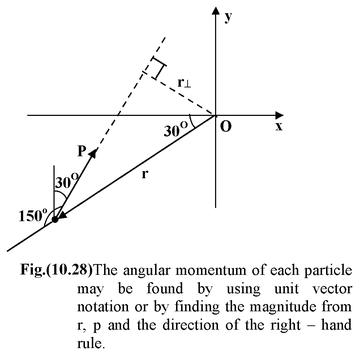
What is the angular momentum of a particle of mass m = 2 kg that is located 15 m from the origin in the direction 30° south of west and has a velocity v = 10 m/s in the direction 30o east of north?
|
Solution
In the figure (10.28 a), the x – axis points east. We know r = 15 m;
(180 o – 30 o ) = 150 o (see figure (10.28 a)). Thus, L = rp sinθ = (15)(20)sin150 o = 150 kg m2/s We could also have used the moment arm r⊥ = 15 sin30 o = 7.5 m L = r⊥p = (7.5) × (20) = 150 kg m/s In unit vector notation,
Therefore, |
|
L = (- 15√3/2i – 15/2 j) × (10i + 10√3j) = −150 k kg m2/s
Note that angular momentum is defined always with respect to a point.
|
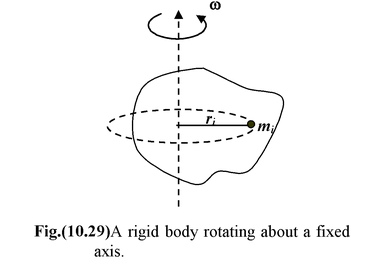
The total angular momentum
Since
therefore, L = Σripi Also pi = mivi = miriω or L = Σmiri2 ω or L = Iω (10.34) where I = Σm i r i 2 |
|
Example 10.21
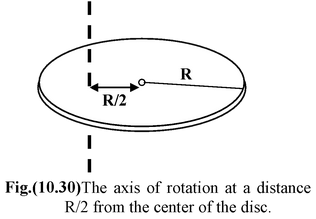
A disc of mass M and radius R rotating at an angular velocity ω about an axis perpendicular to its plane at a distance R/2 from the center, as shown in the figure (10.28). What is its angular momentum? The moment of inertia of a disc about the central axis is MR 2 /2.
Solution
The moment of inertia of the disc about the given axis may be found from the parallel axes theorem, equation I = Icm + Mh2, where h is the distance between the given axis and a parallel axis through the center of mass.
|
Here h = R/2, therefore, I = = 3MR 2 /4 The angular momentum is L = Iω = 3MR 2 ω/4 |
|
What changes the Angular Momentum?
As force changes the linear momentum of a particle, torque changes the angular momentum of a particle. The rate of change of angular with time is given by
(10.35)
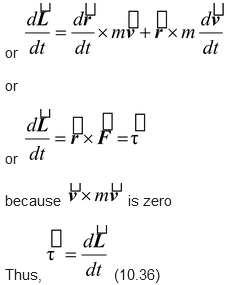
The above equation is the rotational analog of equation
Example 10.22
Show that equation (10.36) can be applied to the motion of a projectile.
Solution
In figure (10.30) , we take the initial point as the origin. At a later time, r = xi + yj.
Since the force on the particle is F = −mgj, the gravitational torque on it is
τ = (xi + yj) × (−mgj) = −mgx k
The rate of change of the angular momentum L = r × p is
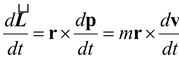
But the acceleration is dv/dt = -gj. Thus
= −mgx k
Hence the equation (10.32) is applicable
Example 10.23
Two blocks with masses m1 = 3 kg and m2 = 1 kg are connected by a rope that passes over a pulley of radius
R = 0.2 m and mass M = 4 kg. The moment of inertia of the pulley about its center is I = MR
2
/2. Use the concept of angular momentum to find the linear acceleration of the blocks. There is no friction. Assume that the c.m. of the block of mass m2 is at a distance R above the center of the pulley.
Solution
If we take the origin at the center of the pulley, the angular momenta of the blocks are m1vR and m2vR and that of the pulley is Iω. Therefore, the total angular momentum is
L = m 1 vR + m 2 vR + Iω (i)
If the rope does not slip, then v = ωR.
∴ L = (m 1 + m 2 )vR + MR/2V
The net external torque about the center of the pulley is due to the weight of m1
τext = r ⊥ F = R(m 1 g) (ii)
Applying equation (10.32),
We obtain
Rm 1 g = (m 1 + m 2 )Ra +
or a =
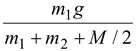
putting m 1 = 3 kg; m 2 = 1 kg; M = 4 kg; R = 0.2 m
a = = 5 m/s 2
Conservation of Angular Momentum
If the net external torque on a system is zero, the total angular momentum is constant in magnitude and direction.
That is, if
Thus, L = constant
For rigid body rotating about a fixed axis,
Lf = Li
or Ifωf = Iiωi (10.37)
Angular Impulse
In complete analogy with the linear momentum, angular impulse is defined as
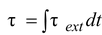
Using Newton’s second law for rotation motion,
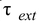 = dL/dt
= dL/dt
∴
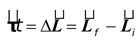
The net angular impulse acting on a rigid body is equal to the change in angular momentum of the body. This is called the impulse – momentum theorem for rotational dynamics.
Example 10.24
A disc of moment of inertia 4 kg m2 is spinning freely at 3 rad/s. A second disc of moment of inertia 2 kg m2 slides down the spindle and they rotate together.
(a) What is the angular velocity of the combination?
(b) What is the change in kinetic energy of the system?
Solution
Since there are no external torques acting, we may apply the conservation of angular momentum.
Ifωf = Iiωi
(6 kg m2)ωf = (4 kg m2)(3 rad/s)
Thus, ωf = 2 rad/s
(b) The kinetic energies before and after the collision are
Ki = J;
Kf = J
The change is
ΔK = Kf – Ki = -6 J.
In order for the two discs to spin together at the same rate, there had to be friction between them. The lost kinetic energy is converted with thermal energy.
Table 10.3 Analogy between Rotational Dynamics and Linear Dynamics.
|
Quantity |
Linear |
Rotational |
|
1. Inertia |
m |
or
|
|
2. Newton’s Second Law |
Fext = ma
|
|
|
3. Work |
Wlin =
|
Wrot =
|
|
4. Kinetic Energy |
Klin =
|
Krot =
|
|
5. Work Energy Theorem |
Wlin = ΔKlin |
Wrot = ΔKrot |
|
6. Impulse |
I = ∫ F ext dt |
J = ∫
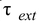 dt
dt
|
|
7. Momentum |
p = mv |
L = Iω |
|
8. Impulse Momentum Theorem |
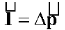
|
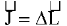
|
|
9. Power |
P =
|
P =
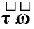
|
Example 10.25
A man of mass m = 80 kg runs at a speed u = 4 m/s along the tangent to a disc-shaped platform of mass M = 160 kg and radius R = 2m. The platform is initially at rest but can rotate freely about an axis through its center. Take
I = MR
2
/2
(a) Find the angular velocity of the platform after the man jumps on.
(b) He then walks to the center. Find the new angular velocity. Treat the man as a point particle.
Solution
Can we apply the conservation of linear momentum?
No, it cannot be applied because the axle exerts an external force on the system
man + platform.
Can we apply the conservation of angular momentum! Yes, since the axle does not exert any torque, we may use the conservation of angular momentum.
Can we apply kinetic energy for the collision between the man and the platform? Why?
(a) We choose the origin at the center of platform as shown in figure(10.34). When the man runs in a straight line, his initial angular momentum about this origin is L = r⊥p,
where in this case r⊥ = R
so Li = muR
After he jumps on, one must take into account his contribution mR2 to the moment of inertia. The final angular momentum, L =Iω, is
Lf =
When we use set Lf = Li , we find
ω =
putting m = 80 kg; M = 160 kg; u = 4 m/s; R = 2 m
We get ω =
(b) When the man reaches the center, his contribution to the moment of inertia is zero. The final angular momentum of part (a) is the initial value for (b):
Li =
Lf = ω2 = 320 ω 2
Applying angular momentum conservation
Lf = Li
we get ω2 = 2 rad/s
Example 10.26
A wheel is held by a handle on its axle and given an initial angular velocity ωo. The wheel is then placed in contact with the ground. At first the wheel remains stationary, spinning in place. After a short time it begins to move forward and eventually reaches the point where it rolls without slipping. Find the final velocity of the wheel in terms of the initial angular velocity ωo. Take I = .
Solution
We assume that wheel is initially rotating clockwise. Let the wheel starts rolling after a time t. Then,
Using Impulse – Momentum Theorem
For translation
Impulse = Δp = pf – pi
or f t = Mv – 0 (i)
For rotation
Angular Impulse = ΔL = Lf – Li
or -f Rt = Iω - Iωo
Note that clockwise angular momentum is considered as positive.
Since I = , therefore, −fRt = MR 2 /2(ω - ωo) (ii)
Condition of pure rolling
v = ωR (iii)
Using equations (i), (ii) and (iii), we get
−MωR 2 = (ω - ωo)
or ω =
The linear momentum of the wheel is v = ωR
Spin and Orbital Angular Momentum
For a rigid body undergoing linear and rotational motion, the total angular momentum may be split into two parts – the orbital angular momentum and the spin angular momentum. The orbital angular momentum is the angular momentum of the center of mass motion about an origin O in an inertial frame.
The spin angular momentum is the angular momentum relative to the center of mass.
The orbital term treats the system as a point particle at the center of mass, whereas the spin term is the sum of the angular momenta of the particles relative to the center of mass. The total angular momentum relative to the origin O in an inertial frame is the sum:
Example 10.27
A solid sphere of mass M and radius R rolls without slipping on a horizontal surface as shown in the figure. Find the total angular momentum of the sphere with respect to the origin O fixed on the ground.
Solution
Let us assume the clockwise sense of rotation positive.
Orbital angular momentum about O is
Lo = MvR
Spin angular momentum about c.m. is
Lc.m. = Iω =
The total angular momentum is
L = L o + Lcm = M v R + MR 2 ω
For pure rolling, v = ωR, therefore, L =

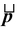 and is located at position
and is located at position
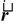 relative to an origin O, as shown in the figure (10.27). Its angular momentum about the origin is defined as
relative to an origin O, as shown in the figure (10.27). Its angular momentum about the origin is defined as
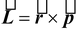 (10.32)
(10.32)
 of a system of particles relative to a given origin is the sum of the angular momentum of the particles.
of a system of particles relative to a given origin is the sum of the angular momentum of the particles.
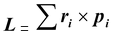
 and
and
 are perpendicular,
are perpendicular,