Introduction

Any motion, which repeats itself in equal intervals of time is called periodic motion. Oftenly, the displacement of a particle in periodic motion can always be expressed in terms of sine and cosine functions. Since the term harmonic is applied to expressions containing these functions, periodic motion is also called harmonic motion.

If a particle in periodic motion moves back and forth (or to and fro) over the same path, then its motion is called oscillatory or vibratory. The examples of oscillatory or vibratory motion are:

• The motion of a pendulum
• The motion of a spring fixed at one end, which is stretched or compressed and then released
• The motion of a violin string
• The motion of atoms in molecules or in a solid lattice
• The motion of air molecules as a sound wave passes by

Characteristics of a Harmonic Motion

The basic quantities characterizing a periodic motion are the amplitude, period and frequency of vibrations.

Amplitude (A)

The amplitude of oscillations is the maximum displacement of a vibrating body from the position of equilibrium.

Time Period (T)

The time period of oscillations is defined as the time between two successive identical positions passed by the body in the same direction.

Frequency (f)

The frequency of oscillations is the number of cycles of vibrations of a body completed in one second. The frequency is related to the time period as

f = 1/T (13.1)

The SI unit of frequency is s-1 or Hz (hertz)

In mechanical oscillations a body oscillates about its mean position which is also its equilibrium position. At the equilibrium position no net force (or torque) acts on the oscillating body. The displacement (linear or angular) of an oscillating particle is its distance (linear or angular) from the equilibrium position at any instant.

When a body oscillates along a straight line within two fixed limits; its displacement x changes periodically in both magnitude and direction; its velocity v and acceleration a also vary periodically in magnitude and direction, shown in fig.(13.1). Since F = ma, therefore, the force acting on the body also varies in magnitude and direction with time.

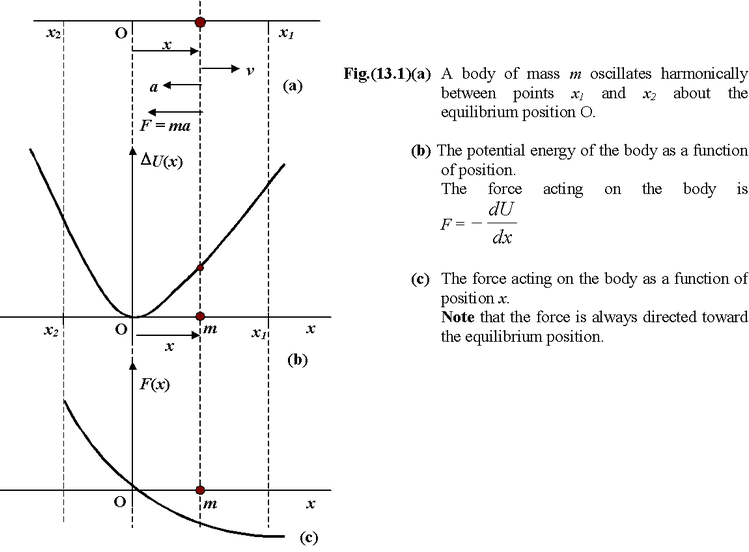
In terms of energy, we can say that a particle executing harmonic motion moves back and forth about a point at which the potential energy is minimum (equilibrium position). The force acting on the body at any position is given by

F = -dU/dx (13.2)

When a body is displaced from its equilibrium it is acted upon by a restoring force (or torque) which always acts to accelerate the body in the direction of its equilibrium position as shown in the figure.