
Measurement And Units
Units And Dimensions of Class 11
Physical Quantity
Any meaningful term which can be measured is a physical quantity. For example length, velocity, time etc. are physical quantity. But handsomeness, beauty are not physical quantity. Why measurement is needed?: Physics is an experimental science and experiments involve measurement of different physical quantities in which laws of physics are expressed. Without measuring results of experiments, it would not be possible for scientists to communicate their results to one another or to compare the results of experiments from different laboratories.
| Table of Content |
Units of Measurement
To measure a physical quantity we need some standard unit of that quantity. For example, if a measurement of length is quoted as 5 meters, it means that the measured length is 5 times as long as the value accepted for a standard length defined to be “one meter”.
Any set of standards of units must fulfill the following two conditions
- It must be accessible.
- It must be invariable with the passage of time
Two more auxiliary conditions
- It is necessary to have wide unlimited agreement about those standards.
- It is inter convertible to different units of same quantity.
A measurement consists of two parts, one is numeric and the other is standard chosen. For example, 5 meter of length implies 5 times the “standard meter”. It is not necessary to establish a measurement standard for every physical quantity. Some quantities can be regarded as fundamental and the standard for other quantities can be derived from the fundamental ones. For example, in mechanics length, mass and time are regarded as fundamental quantities and the standard for speed (= length / time) can be derived from fundamental quantities length and time.
| Quantity | SI Units | Symbols |
| Time | second | s |
| Length | meter | m |
| Mass | kilogram | kg |
| Amount of Substance | mole | mol |
| Thermodynamic Temp. | kelvin | K |
| Electric Current | ampere | A |
| Luminous Intensity | candela | Cd |
Two Supplementary Units
| Plane Angle | Radian | rad |
| Solid Angle | Steradian | sr |
- Two other system of units compete with the international system- One is Gaussian System in terms of which much of the literature of physics is expressed. In India this system is not in use.
- The other is the British system- This system is still in daily use in United states and United Kingdom. But SI units are standard units worldwide.
- C.G.S. Unit- In this system of unit, centimeter, gram and seconds are units of length, mass and time respectively.
- Conversion of One System of Units to another System- The basic formula is n 1 u 1 = n 2 u 2 where n 1 and n 2 are numbers.
Q1. How many dyne−centimeter are equal to 1 N −m ?
Ans. 1N -m = (1 kg)(1m 2 ) (1s -2 )
1 dyne - centimeter = (1kg)(1cm 2 )(1 s -2 )
1N -M / 1 dyne -cm = (1000g/1g)(100cm 2 / 1cm)
= 1000 x 10000
1N -m = 107 dyne -cm
Measurement of Length
Depending upon the range of length, there are three main methods for measuring length:
- Direct method
- Indirect or Mathematical method
- Chemical Mehtod
Direct method
The simplest method measuring the length of a straight line is by means of a meter scale. But there exist some limitations in the accuracy of the result:
- The dividing lines have a finite thickness.
- Naked eye cannot correctly estimate less than 0.5 mm
For greater accuracy devices like
- Vernier calliper
- micrometer scale (screw gauge)
Vernier Calliper
It consists of a main scale graduated in cm/mm over which an auxiliary scale (or Vernier scale) can slide along the length. The division of the Vernier scale being slightly shorter than the divisions of the main scale.
Vernier Calliper Least count
The least count or the Vernier constant (V.C.) is the minimum value of correct estimation of length without eye estimation. The difference between the values of one main scale division and one vernier scale division is known as vernier constant if N division of vernier scale coincides with (N−1) divisions of main scale, then vernier constant,
n.V.S.D. = (n −1 ) M.S.D.
1.V.S.D. = (n -1 / n) M.S.D., then
LC = 1.M.S.D. − 1.V.S.D. = 1.M.S.D. (n -1 / n) M.S.D.
=1/n M.S.D.
Vernier Calliper Least Count Formula = Smallest Division on main scale / No. of division on vernier scale
Vernier Calliper Reading
Let one main scale division be 1 mm and 10 vernier scale divisions coincide with 9 main scale divisions
1.V.S.D. = 9/10 M.S.D.=0.9 mm
Vernier constant = 1.M.S.D − 1.V.S.D. = 1 mm − 0.9 mm
= 0.1 mm = 0.01 cm
The reading with vernier scale is read as given below :
- Firstly take the main scale reading (N) before on the left of the zero of the vernier scale.
- Find the number (n) of vernier division which just coincides with any of the main scale division. Multiply this number (n) with vernier constant (V.C.)
- Total reading = (N + n × V.C.)
Caution: The main scale reading with which the Vernier scale division coincides has no connection with reading
Suppose If we have to measure a length AB, the end A is coincided with the zero of the vernier scale as shown in fig. Its enlarged view is given in fig.
1.0 cm < Length AB < 1.1. cm
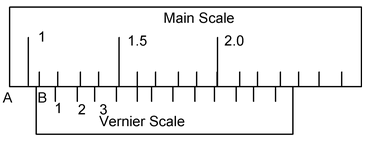
Let 5th division of vernier scale coincide with 1.6 cm of main scale. From diagram it is clear that the distance between 4th division of vernier scale and 1.5 cm of main scale is equal to one V.C. and distance between zero mark of vernier scale and 1.0 cm mark on the main scale is equal to 5 times the vernier constant.
AB = 1.0 + 5 × L.C. = 1.0 + 5 × 0.01 = 1.05 cm.
Q2. In travelling microscope the vernier scale used has the following data. 1 M.S.D. = 0.5 mm, 50 V.S.D. = 49 M.S.D. and the actual reading for distance travelled by travelling microscope is 2.4 cm with 8th division coinciding with a main scale graduation . Estimate the distance travelled.
Ans. In this case vernier constant = 1.M.S.D. − 1.V.S.D.
= 1.M.S.D. − 49/50 M.S.D.
= 1/50 M.S.D
=1/50 x 0.5 mm
= 5/10 x 1/50 = 0.01mm = 0.001cm
Distance travelled = 2.4 + 8 × 0.001 cm
= 2.408 cm
Q3. The Vernier scale used in Fortin’s barometer has 20 divisions coinciding with the 19 main scale divisions. If the height of the mercury level measured is 5 mm and 15th division of vernier scale is coinciding with the main scale division. Then calculate the exact height of the mercury level (given that 1.M.S.D. = 1mm)
Ans. 20 V.S.D. = 19 M.S.D. (Given)
1.V.S.D. = 19/20 M.S.D
V.C. = 1. M.S.D. − 1.V.S.D = (1 - 19/20M.S.D.)
= 1/20 M.S.D.
= 1/20 x 1 mm
= 0.005 cm
Height of mercury level = 5 + 0.05 × 15
= 5.75 mm.
Zero Error
If the zero marking of main scale and Vernier scale do not coincide, necessary correction has to be made for this error which is known as zero error of the instrument. If the zero of the vernier scale is to the right of the zero of the main scale the zero error is said to be positive and the correction will be negative and vice versa.
Q1. Consider the following data:
10 main scale divisions = 1cm, 10 vernier division = 9 main scale divisions, zero of Vernier scale is to the right of the zero marking of the main scale with 6th Vernier division coinciding with a main scale division and the actual reading for length measurement is 4.3 cm with 2nd Vernier divisions coinciding with a main scale graduation. Estimate the length.
Ans. In this case, vernier constant = 1mm/100
Zero error = 6 × 0.1 = + 0.6 mm
Correction = −0.6 mm
Actual length = (4.3 + 2 × 0.01) + correction
= 4.32 − 0.06 = 4.26 cm.
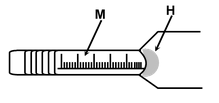
Screw Gauge (or Micrometer Screw)
In general Vernier Callipers can measure accurately upto 0.02 mm and for greater accuracy micrometer screw devices, e.g. screw gauge, spherometer are used. These consist of accurately cut screw which can be moved in a closely fitting fixed nut by turning it axially. The instrument is provided with two scales:
- The main scale or pitch scale M graduated along the axis of the screw.
- The cap−scale or head scale H round the edge of the screw head.
Constants of the screw gauge
- Pitch: The translational motion of the screw is directly proportional to the total rotation of the head. The pitch of the instrument is the distance between two consecutive threads of the screw which is equal to the distance moved by the screw due to one complete rotation of the cap. Thus if 10 rotations of cap ≡5 mm, then pitch = 0.5 mm
In general, pitch = Distance travelled by screw on main scale / No. of rotation taken by the cap to travel that much distance
- Least count: In this case also, the minimum (or least) measurement (or count) of length is equal to one division on the main scale which is equal to pitch divided by the total cap divisions. Thus in the aforesaid Illustration, if the total cap division is 100, then least count = 0.5 mm/100
= 0.005 mm
In general, In case of circular scale,
Least count = Pitch / Number of division on circular scale
If pitch is 1 mm and there are 100 divisions on circular scale, then
Least count = 1mm/100 = 0.01 mm = 0.001 cm
= 0.00001 m = 10−5 m = 10 μm
Since least count is of the order of 10 μm, So the screw is called a micrometer screw. Screw gauge and the spherometer which work on the principle of micrometer screw, consist essentially of the following two scales.
- Linear or Pitch scale: It is a scale running parallel to the axis of the screw.
- Circular of Head scale: It is marked on the circumference of the circular disc or the cap attached to the screw.
- Zero Error: In a perfect instrument the zero of the head scale coincides with the line of graduation along the screw axis with no zero−error, otherwise the instrument is said to have zero−error which is equal to the cap reading with the gap closed. This error is positive when zero line or reference line of the cap lies below the line of graduation and vice−versa. The corresponding corrections will be just opposite.
Q1. A screw gauge has 100 divisions on its circular scale. Circular scale travels one division on linear scale in one rotation and 10 divisions on linear scale of screw gauge is equal to 5 mm. What is the least count of a screw gauge.
Ans. Pitch = 1 division on linear scale / 1 rotation = 1 div
10 division = 5 mm
1 division = 0.5 mm
pitch = 0.5 mm
least count = Pitch / No. of divisions on circular scale
= 0.5 mm /100
= 0.005 mm
Q2. The screw gauge mentioned in above illustration is used to measure thickness of a coin. The reading of the linear scale is 4th div and 25th division of circular scale is coinciding with it. What is the value of thickness of the coin.
Ans. Reading = Linear scale Reading + Least count × circular scale reading
= 4th division on linear scale + 0.005 mm × 25
= 4 × 0.5 mm + 0.125 mm
= 2 mm + 0.125 mm
= 2.125 mm
Q3. A spherometer has 250 equal divisions marked along the periphery of its disc and one full rotation of the disc advances it on the main scale by 0.0625 cm. The least count of the spherometer is
(A) 2.5x10 −2 cm
(B) 25 x10 −3 cm
(C) 2.5x10 −4 cm
(D) none of the above
Ans. Correct option is (C)
Least count = 0.0625/250 cm = 2.5 x 10 −4 cm
Indirect or Mathematical method
This method involves measurement of long distances. Main methods of this category are −
Reflection method: Suppose we want to measure the distance of a multi story building from a destination point P. If a shot be fired from P, the sound of shot travels a distance x towards the building, gets reflected from the building. The reflected sound travels the distance x to the point of P, when an echo of the shot is heard.
Let t = time interval between the firing of the shot and echo sound.
v = velocity of sound in air.
Distance = velocity x time
x + x = (v) (t)
⇒ x = (v) (t/2)
As v is known, x can be calculated by measuring the time t.
Q8. A rock is at the bottom of a very deep river. An ultrasonic signal is sent towards rock and received back after reflection from rock in 4 seconds. If the velocity of ultrasonic wave in water is 1.45 km/s, find the depth of river.
Ans. Here x = ?
v = 1.45 km/s = 1450 m/sec.
t = 4 sec
so, x = v x t / 2 = 1450 x 4 / 2 = 2900 m.
- Parallel method: This method is used for measuring the distance of nearby stars. If we have to measure the distance D of a faraway star S by this method. We observe this star from two different positions A and B on the earth, separated by a distance AB = b at the same time as shown in the figure. Let ∠ASB =θ, the angle θ is called parallatic angle. As the star is very far away, b/D << 1 and θ is very small.
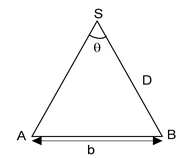
Here we can take AB as an arc of length b of a circle with center at S and the distance D as the radius AS=BS so that AB = b = Dθ where θ is in radians.
D = b/θ
Knowing b and measuring θ, we can calculate D.
- Copernicus method: This method is used to measure the relative distances of the planets from the Sun.
- For Interior Planets: The angle formed at earth between the earth−planet direction and the earth−sun direction is called the planet’s elongation. This is the angular distance of the planet from the sun as observed from earth. When the elongation attains its maximum value ε as in the figure, the planet appears farthest from Sun.
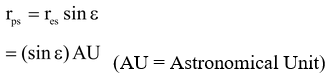
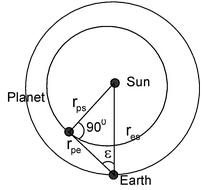
- For Exterior Planets: This method is a consequence of Kepler’s 3rd law of planetary motion. For two planets P 1 and P 2 we have,
a 3 2 / a 3 1 = T 2 2 / T 2 1
where a 1 and a 2 are semi−major axes, of respective orbits. The period can be ascertained by direct observation. Therefore if a 1 is measured, a 2 can be calculated.
Chemical Method
This method is used to measure the distance of the order of 10−10 m. Let us calculate the size of an atom.
Let m = mass of substance,
V = volume occupied by substance &
ρ = density of the substance
v = m /ρ (1)
Let M be the atomic weight of the substance and N be the Avogadro number.
No. of atoms in mass m of the substance = Nm / M
If r = radius of each atom then V = volume of each atom = 4/3 πr 3
Volume of all the atoms in substance = (4/3 πr 3 x Nm)/M.
According to Avagordo’s hypothesis,
Volume of all the atoms = (2/3) x volume of substance
4/3 πr 3 x Nm/M = (2/3) m/ρ
r = (M/2πNρ) 1/3
Frequently Asked Question (FAQs)
Q1. What is Vernier Calliper?
Ans. A measuring device is used for the measurement of linear dimensions. It is also used to measure the diameters of round objects with the help of the measuring jaws.
Q2. What is the least count of Vernier callipers?
Ans. The zero mark of the Vernier scale has gone seven-tenths of a millimeter past the 11.0 mm mark, giving a total reading of 11.7 mm. The least count of the Vernier caliper is 0.1 mm. 0.1 mm is the smallest scale reading that can be made without estimation.
Q3. What is the atomic mass unit (AMU) of 1 Å?
Ans. 1 A.U. = 1.496 × 10 11 m and 1 Å = 10 10 m.
Q4. Are S.I. units Coherent? Why?
Ans. Yes, because all the derived units in this system can be obtained by multiplying or dividing a certain set of basic units.









