
Theorems of Moment of Inertia are important tools in the realm of engineering mechanics, specifically when dealing with the calculation of moments of inertia for various composite geometrical shapes.
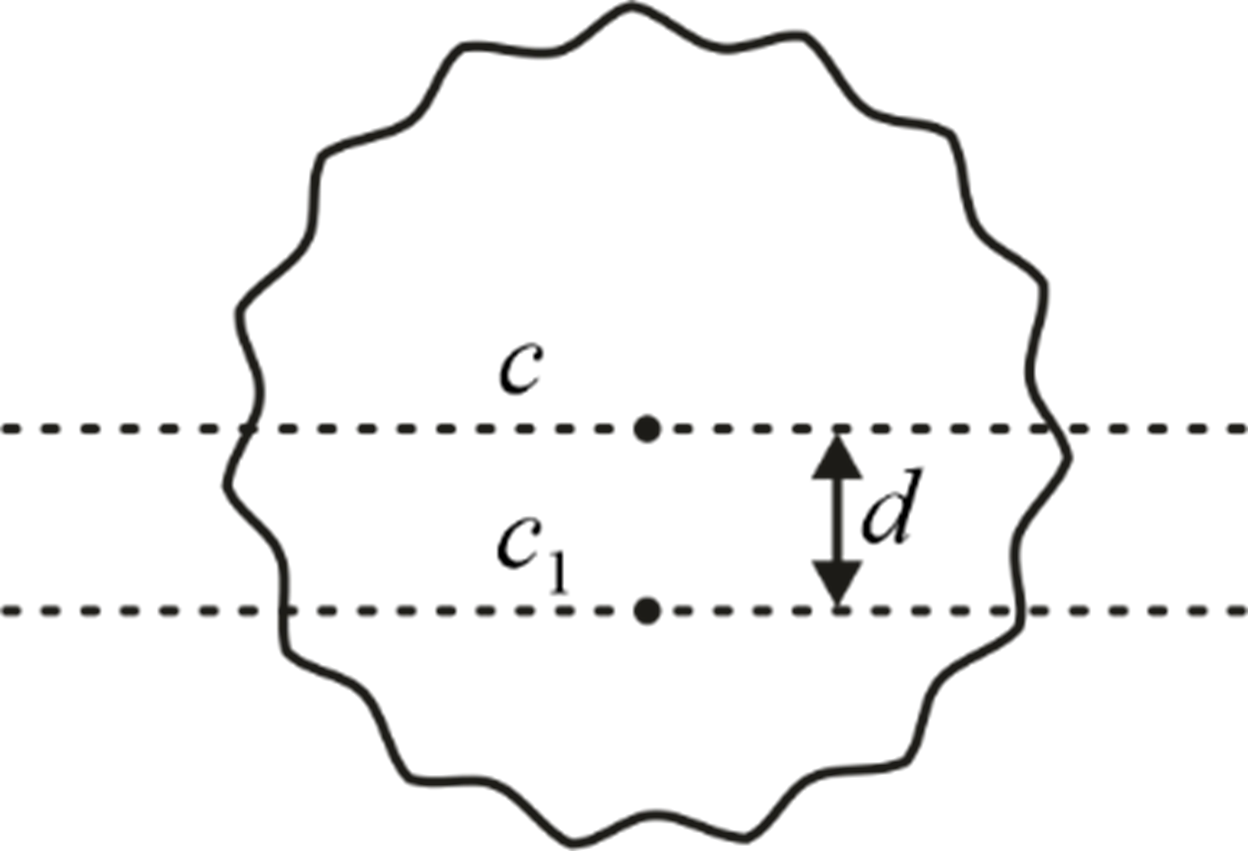
For the object shown, moment of inertia about an axis passing through point c 1 is:
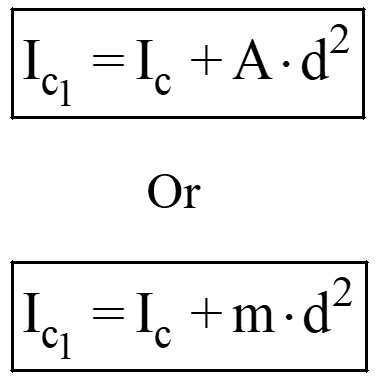
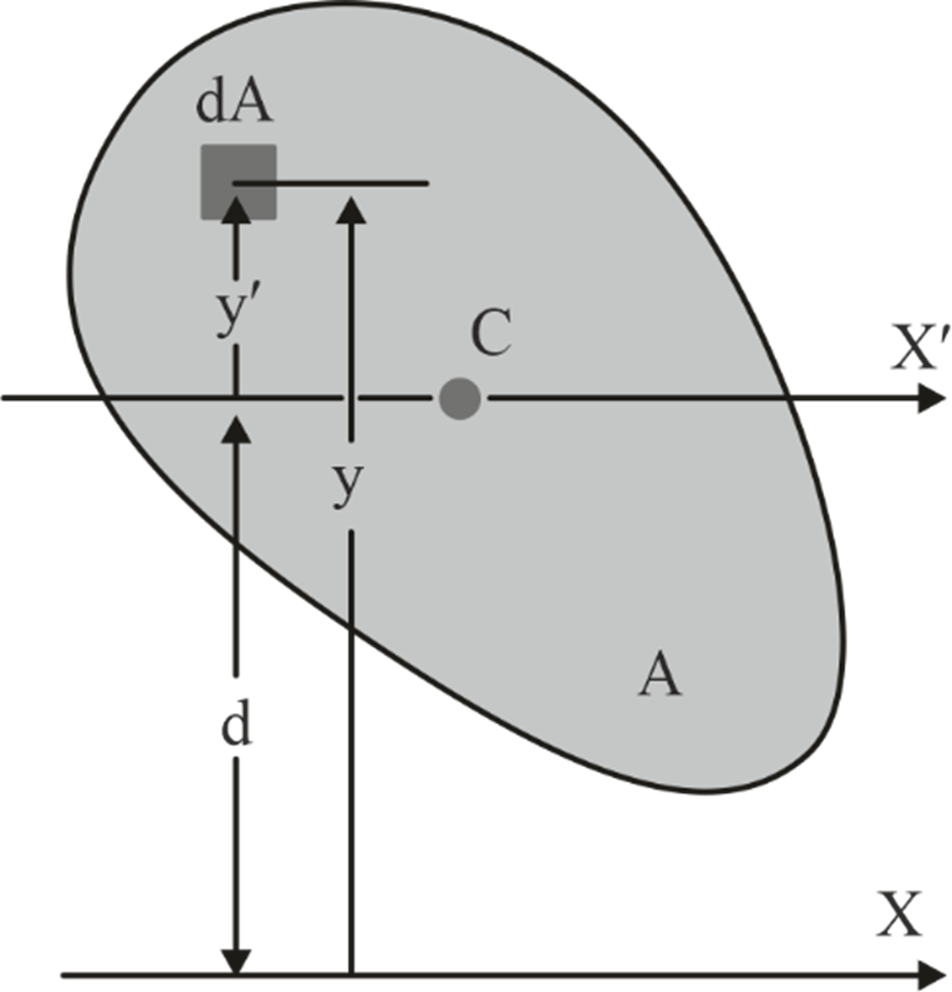
To establish this theorem, let's examine a two-dimensional plane denoted by area A, with its centroid marked as point c, as shown in Figure. We have a Cartesian axis, X. Additionally, we have a parallel axis, X’, that passes through the centroid c of the plane.
Here, d is the distance between X and the X' axis, and y’ is the distance of elemental area dA from the X’ axis. Let’s focus on the elemental area dA.
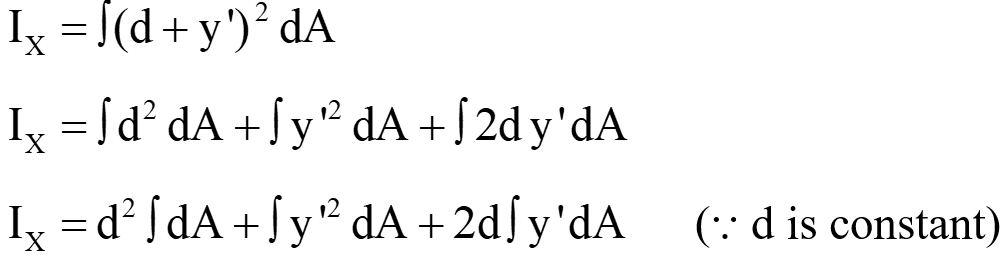 Put the values in above equation (∫dA = A and ∫y′
2
dA = I
X′
or I
c
and ∫y′dA=0 )
Put the values in above equation (∫dA = A and ∫y′
2
dA = I
X′
or I
c
and ∫y′dA=0 )
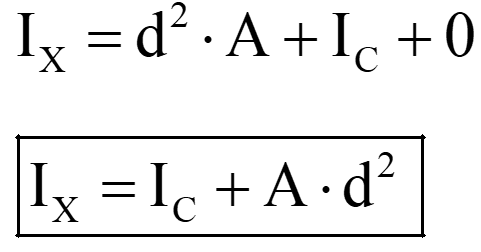
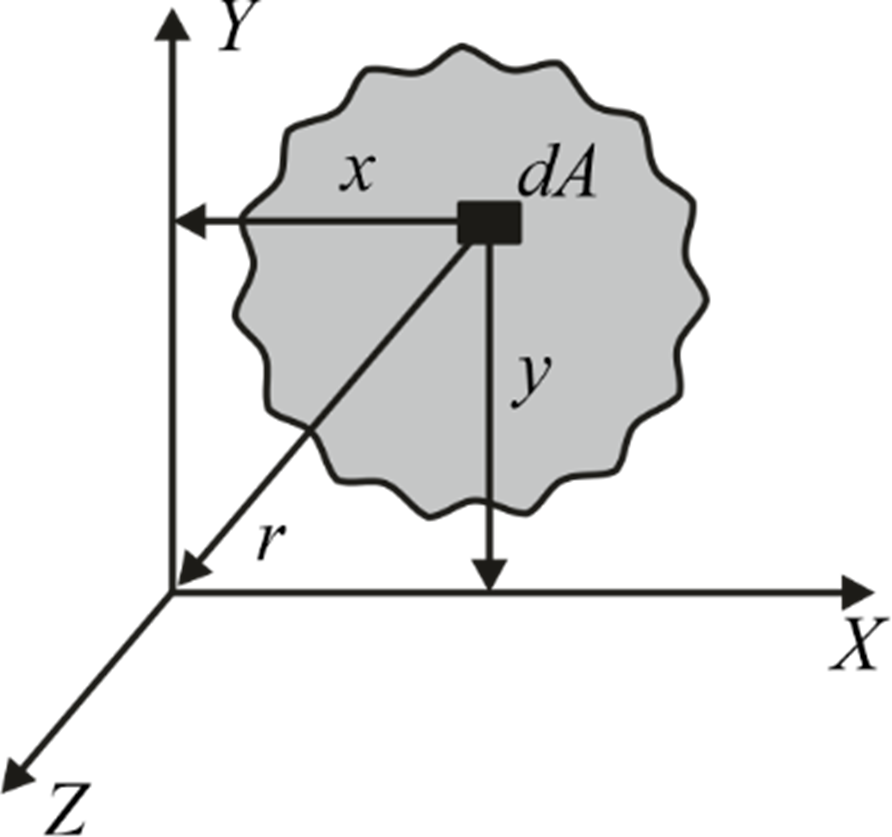
To establish this theorem, let's examine a two-dimensional plane denoted by area A. We have a Cartesian axis, x and y. Here, x, y, and r are the distances of elemental area dA from the X, Y, and Z axes. Let’s focus on the elemental area dA.
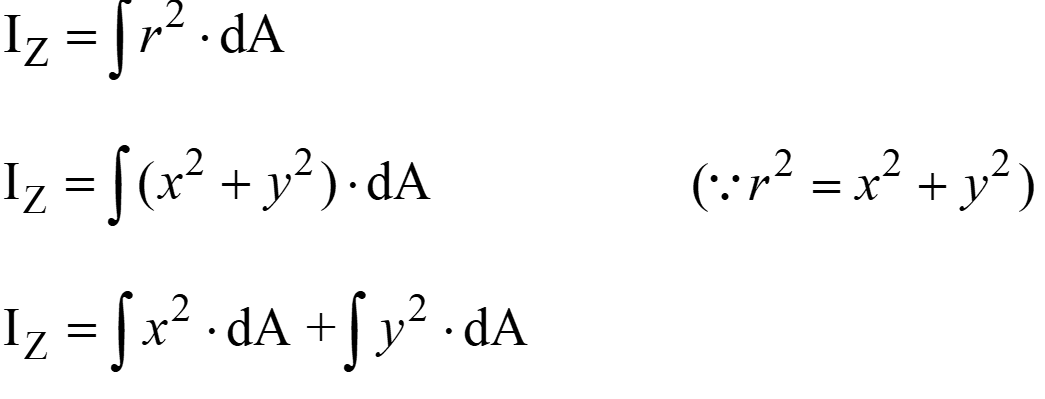 Put the values in above equation (∫x
2
dA = I
X
and ∫y
2
dA = I
Y
)
Put the values in above equation (∫x
2
dA = I
X
and ∫y
2
dA = I
Y
)
![]()
Note: This theorem is very helpful to calculate the polar moment of inertia.
Limitation: The limitation of the perpendicular axis theorem is that it can only be applied to planar shapes that lie within a single plane. This theorem is not valid for three-dimensional objects that extend in multiple directions.