
Absolute value formulas: It's essential to review the concept of absolute value. Absolute value measures a number's distance from zero on a number line. This measurement always results in a positive number or zero; it's never negative. We use the symbol |x| to represent the absolute value of a number "x," and Sometimes, you may come across the terms "mod x" or "modulus of x" to describe the same concept. So, when we find the absolute value of a number, we are finding its distance from zero, and that distance is always a positive value.
The absolute value formula helps us find the absolute value of any number, ensuring that the result is always positive. This formula is best explained through an example:
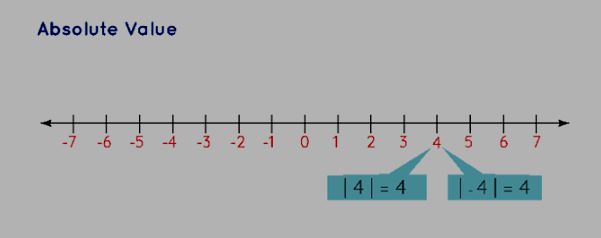
In the example above, when we calculate |4|, it equals 4. Therefore, we can conclude that |x| = x for all x values equal to or greater than 0.
Similarly, when we calculate |-4|, it equals 4. As a result, we can conclude that |-4| equals -(-4), which simplifies to 4. Therefore, we can state:
|x| = -x for every x less than 0.
|x| = x for every x greater than or equal to 0.
This is the formula for Absolute Value.'
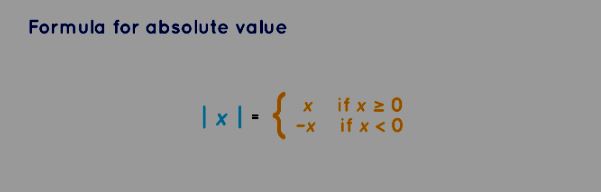
Example 1: Finding Absolute Values
Let's apply the absolute value formula to find the absolute values of -1/3, 5, and -0.5:
|-1/3| = 1/3
|5| = 5
|-0.5| = 0.5
So, the absolute values are |-1/3| = 1/3, |5| = 5, and |-0.5| = 0.5.
Example 2: Finding Solutions for the Equation |x| = 5
Now, let's solve the equation |x| = 5 using the absolute value formula:
Given equation: |x| = 5
According to the absolute value formula, |x| can be either +x or -x, depending on the sign of x. Therefore, we have:
+x = 5
-x = 5
Solving these equations separately:
For +x = 5, x = 5
For -x = 5, x = -5
The solutions to the equation |x| = 5 are x = 5 and x = -5.
Example 3: Find the absolute values of the following numbers: -2, 0, and 3.
Using the absolute value formula:
|-2| = 2
|0| = 0
|3| = 3
So, the absolute values are |-2| = 2, |0| = 0, and |3| = 3.
Example 4: Solving the Equation |x| = 10 Using the Absolute Value Formula
Given equation: |x| = 10
According to the absolute value formula:
+x = 10
-x = 10
Solving these equations separately:
For +x = 10, x = 10
For -x = 10, x = -10
The solutions to the equation |x| = 10 are x = 10 and x = -10.
Example 5: Calculate the absolute value of the difference between two numbers, a = 7 and b = 15.
Using the absolute value formula to find |a - b|:
|7 - 15| = |-8| = 8
So, the absolute value of the difference between 7 and 15 is 8.
Example 6: Determine the absolute value of a negative fraction, -1/4.
Using the absolute value formula:
|-1/4| = 1/4
Now, the absolute value of -1/4 is 1/4.
Example 7: Solve the absolute value equation |2x - 1| = 7 using the absolute value formula.
Given equation: |2x - 1| = 7
According to the absolute value formula:
2x - 1 = 7
-(2x - 1) = 7
Solving these equations separately:
For 2x - 1 = 7, 2x = 8, x = 4
For -(2x - 1) = 7, -2x + 1 = 7, -2x = 6, x = -3
Now, the solutions to the equation |2x - 1| = 7 are x = 4 and x = -3.
Example 8: Find the solutions to the equation |3x - 2| = 8.
Solution:
We will consider two cases:
Case 1: 3x - 2 is positive or zero:
3x - 2 = 8
Now, solve for x:
3x = 8 + 2
3x = 10
x = 10/3
Case 2: 3x - 2 is negative:
-(3x - 2) = 8
Now, solve for x:
-3x + 2 = 8
-3x = 8 - 2
-3x = 6
x = 6/(-3)
x = -2
So, the solutions to the equation |3x - 2| = 8 are x = 10/3 and x = -2.
